河北省中考数学真题汇编（近几年） 4 图形的性质

更新时间：2021-08-20 浏览次数：130 类型：二轮复习

一、单选题

1. (2024八下·象山期中) 如图，菱形ABCD中，∠D＝150°，则∠1＝（）

A . 30° B . 25° C . 20° D . 15°

答案解析收藏纠错 + 选题
2. (2023九下·齐齐哈尔开学考) 一个骰子相对两面的点数之和为7，它的展开图如图，下列判断正确的是（）

A . $\text{[math]}$ 代表 B . $\text{[math]}$ 代表 C . $\text{[math]}$ 代表 D . $\text{[math]}$ 代表

答案解析收藏纠错 + 选题
3. (2022·柳南模拟) 如图，已知四条线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 中的一条与挡板另一侧的线段 $\text{[math]}$ 在同一直线上，请借助直尺判断该线段是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2021·河北) 如图1， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 为锐角．要在对角线 $\text{[math]}$ 上找点 $\text{[math]}$ ， $\text{[math]}$ ，使四边形 $\text{[math]}$ 为平行四边形，现有图2中的甲、乙、丙三种方案，则正确的方案（）

图2

A . 甲、乙、丙都是 B . 只有甲、乙才是 C . 只有甲、丙才是 D . 只有乙、丙才是

答案解析收藏纠错 + 选题
5. (2021·河北) 如图，点 $\text{[math]}$ 为正六边形 $\text{[math]}$ 对角线 $\text{[math]}$ 上一点， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的值是（）

A . 20 B . 30 C . 40 D . 随点 $\text{[math]}$ 位置而变化

答案解析收藏纠错 + 选题
6. (2021·河北) 如图，等腰 $\text{[math]}$ 中，顶角 $\text{[math]}$ ，用尺规按①到④的步骤操作：

①以 $\text{[math]}$ 为圆心， $\text{[math]}$ 为半径画圆；

②在 $\text{[math]}$ 上任取一点 $\text{[math]}$ （不与点 $\text{[math]}$ ， $\text{[math]}$ 重合），连接 $\text{[math]}$ ；

③作 $\text{[math]}$ 的垂直平分线与 $\text{[math]}$ 交于 $\text{[math]}$ ， $\text{[math]}$ ；

④作 $\text{[math]}$ 的垂直平分线与 $\text{[math]}$ 交于 $\text{[math]}$ ， $\text{[math]}$ ．

结论Ⅰ：顺次连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 四点必能得到矩形；

结论Ⅱ： $\text{[math]}$ 上只有唯一的点 $\text{[math]}$ ，使得 $\text{[math]}$ ．

对于结论Ⅰ和Ⅱ，下列判断正确的是（）

A . Ⅰ和Ⅱ都对 B . Ⅰ和Ⅱ都不对 C . Ⅰ不对Ⅱ对 D . Ⅰ对Ⅱ不对

答案解析收藏纠错 + 选题
7. (2023九上·石家庄期中) 有一题目：“已知；点 $\text{[math]}$ 为 $\text{[math]}$ 的外心， $\text{[math]}$ ，求 $\text{[math]}$ ．”嘉嘉的解答为：画 $\text{[math]}$ 以及它的外接圆 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，如图．由 $\text{[math]}$ ，得 $\text{[math]}$ ．而淇淇说：“嘉嘉考虑的不周全， $\text{[math]}$ 还应有另一个不同的值．”，下列判断正确的是（）

A . 淇淇说的对，且 $\text{[math]}$ 的另一个值是115° B . 淇淇说的不对， $\text{[math]}$ 就得65° C . 嘉嘉求的结果不对， $\text{[math]}$ 应得50° D . 两人都不对， $\text{[math]}$ 应有3个不同值

答案解析收藏纠错 + 选题
8. (2022八下·高阳期末) 如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案．现有五种正方形纸片，面积分别是1，2，3，4，5，选取其中三块（可重复选取）按图的方式组成图案，使所围成的三角形是面积最大的直角三角形，则选取的三块纸片的面积分别是（）

A . 1，4，5 B . 2，3，5 C . 3，4，5 D . 2，2，4

答案解析收藏纠错 + 选题
9. (2021·驻马店模拟) 如图，从笔直的公路 $\text{[math]}$ 旁一点P出发，向西走 $\text{[math]}$ 到达 $\text{[math]}$ ；从P出发向北走 $\text{[math]}$ 也到达l．下列说法错误的是（）

A . 从点P向北偏西45°走 $\text{[math]}$ 到达l B . 公路l的走向是南偏西45° C . 公路l的走向是北偏东45° D . 从点P向北走 $\text{[math]}$ 后，再向西走 $\text{[math]}$ 到达l

答案解析收藏纠错 + 选题
10. (2022·牟平模拟) 如图1，已知 $\text{[math]}$ ，用尺规作它的角平分线．
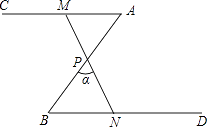
如图2，步骤如下，

第一步：以B为圆心，以a为半径画弧，分别交射线 BA ， BC 于点D，E；

第二步：分别以D，E为圆心，以b为半径画弧，两弧在 $\text{[math]}$ 内部交于点P；

第三步：画射线 BP ．射线 BP 即为所求．

下列正确的是（）

A . a，b均无限制 B . $\text{[math]}$ ， $\text{[math]}$ 的长 C . a有最小限制，b无限制 D . $\text{[math]}$ ， $\text{[math]}$ 的长

答案解析收藏纠错 + 选题
11. (2021八下·薛城期末) 如图，将 $\text{[math]}$ 绕边 $\text{[math]}$ 的中点O顺时针旋转180°．嘉淇发现，旋转后的 $\text{[math]}$ 与 $\text{[math]}$ 构成平行四边形，并推理如下：
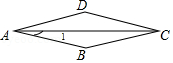
点A，C分别转到了点C，A处，

而点B转到了点D处．

∵ $\text{[math]}$ ，

∴四边形 $\text{[math]}$ 是平行四边形．

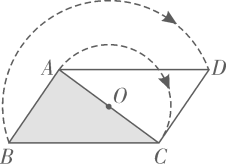
小明为保证嘉淇的推理更严谨，想在方框中“∵ $\text{[math]}$ ，”和“∴四边形……”之间作补充．下列正确的是（）

A . 嘉淇推理严谨，不必补充 B . 应补充：且 $\text{[math]}$ ， C . 应补充：且 $\text{[math]}$ D . 应补充：且 $\text{[math]}$ ，

答案解析收藏纠错 + 选题
12. (2022·易县模拟) 如图，在平面内作已知直线m的垂线，可作垂线的条数有（）

A . 0条 B . 1条 C . 2条 D . 无数条

答案解析收藏纠错 + 选题
13. (2019·河北) 对于题目：“如图1，平面上，正方形内有一长为12、宽为6的矩形，它可以在正方形的内部及边界通过移转（即平移或旋转）的方式，自由地从横放移转到竖放，求正方形边长的最小整数n ． ”甲、乙、丙作了自认为边长最小的正方形，先求出该边长x ，再取最小整数n ．
甲：如图2，思路是当x为矩形对角线长时就可移转过去；结果取n＝13．

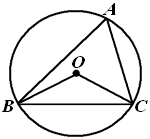
乙：如图3，思路是当x为矩形外接圆直径长时就可移转过去；结果取n＝14．

丙：如图4，思路是当x为矩形的长与宽之和的 $\text{[math]}$ 倍时就可移转过去；结果取n＝13．

下列正确的是（）

A . 甲的思路错，他的n值对 B . 乙的思路和他的n值都对 C . 甲和丙的n值都对 D . 甲、乙的思路都错，而丙的思路对

答案解析收藏纠错 + 选题
14. (2020九上·朝阳期末) 下面是投影屏上出示的抢答题，需要回答横线上符号代表的内容

则回答正确的是（）

A . ◎代表∠FEC B . @代表同位角 C . ▲代表∠EFC D . ※代表AB

答案解析收藏纠错 + 选题
15. (2021·河北) 定理：三角形的一个外角等于与它不相邻的两个内角的和．
已知：如图， $\text{[math]}$ 是 $\text{[math]}$ 的外角．

求证： $\text{[math]}$ ．

下列说法正确的是（）

A . 证法1还需证明其他形状的三角形，该定理的证明才完整 B . 证法1用严谨的推理证明了该定理 C . 证法2用特殊到一般法证明了该定理 D . 证法2只要测量够一百个三角形进行验证，就能证明该定理

答案解析收藏纠错 + 选题

二、填空题

16. (2023八下·萍乡期末) 正六边形的一个内角是正n边形一个外角的4倍，则n=．

答案解析收藏纠错 + 选题
17. (2023八下·洛阳期中) 下图是可调躺椅示意图（数据如图）， $\text{[math]}$ 与 $\text{[math]}$ 的交点为 $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 保持不变．为了舒适，需调整 $\text{[math]}$ 的大小，使 $\text{[math]}$ ，则图中 $\text{[math]}$ 应（填“增加”或“减少”）度．

答案解析收藏纠错 + 选题
18. (2021八下·兴隆期末) 如图，依据尺规作图的痕迹，计算∠α=°．

答案解析收藏纠错 + 选题
19. (2017·河北) 如图，A，B两点被池塘隔开，不能直接测量其距离．于是，小明在岸边选一点C，连接CA，CB，分别延长到点M，N，使AM=AC，BN=BC，测得MN=200m，则A，B间的距离为m．

答案解析收藏纠错 + 选题
20. (2018·河北) 如图1，作∠BPC平分线的反向延长线PA，现要分别以∠APB，∠APC，∠BPC为内角作正多边形，且边长均为1，将作出的三个正多边形填充不同花纹后成为一个图案．例如，若以∠BPC为内角，可作出一个边长为1的正方形，此时∠BPC=90°，而 $\text{[math]}$ =45是360°（多边形外角和）的 $\text{[math]}$ ，这样就恰好可作出两个边长均为1的正八边形，填充花纹后得到一个符合要求的图案，如图2所示．
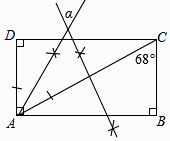
图2中的图案外轮廓周长是；
在所有符合要求的图案中选一个外轮廓周长最大的定为会标，则会标的外轮廓周长是．

答案解析收藏纠错 + 选题

三、综合题

21. (2019·河北) 如图1和2，▱ABCD中，AB＝3，BC＝15，tan∠DAB＝ $\text{[math]}$ ．点P为AB延长线上一点，过点A作⊙O切CP于点P ，设BP＝x ．
1. （1）如图1，x为何值时，圆心O落在AP上？若此时⊙O交AD于点E ，直接指出PE与BC的位置关系；
2. （2）当x＝4时，如图2，⊙O与AC交于点Q ，求∠CAP的度数，并通过计算比较弦AP与劣弧 $\text{[math]}$ 长度的大小；
3. （3）当⊙O与线段AD只有一个公共点时，直接写出x的取值范围．
答案解析收藏纠错 + 选题
22. (2019·河北) 如图，△ABC和△ADE中，AB＝AD＝6，BC＝DE ， ∠B＝∠D＝30°，边AD与边BC交于点P（不与点B ， C重合），点B ， E在AD异侧，I为△APC的内心．
1. （1）求证：∠BAD＝∠CAE；
2. （2）设AP＝x ，请用含x的式子表示PD ，并求PD的最大值；
3. （3）当AB⊥AC时，∠AIC的取值范围为m°＜∠AIC＜n°，分别直接写出m ， n的值．
答案解析收藏纠错 + 选题
23. (2023九上·丛台月考) 如图，∠A=∠B=50°，P为AB中点，点M为射线AC上（不与点A重合）的任意点，连接MP，并使MP的延长线交射线BD于点N，设∠BPN=α．
1. （1）求证：△APM≌△BPN；
2. （2）当MN=2BN时，求α的度数；
3. （3）若△BPN的外心在该三角形的内部，直接写出α的取值范围．
答案解析收藏纠错 + 选题
24. (2018·河北) 如图，点A在数轴上对应的数为26，以原点O为圆心，OA为半径作优弧 $\text{[math]}$ ，使点B在O右下方，且tan∠AOB= $\text{[math]}$ ，在优弧 $\text{[math]}$ 上任取一点P，且能过P作直线l∥OB交数轴于点Q，设Q在数轴上对应的数为x，连接OP．
1. （1）若优弧上一段 $\text{[math]}$ 的长为13π，求∠AOP的度数及x的值；
2. （2）求x的最小值，并指出此时直线l与 $\text{[math]}$ 所在圆的位置关系；
3. （3）若线段PQ的长为12.5，直接写出这时x的值．
答案解析收藏纠错 + 选题
25. (2020·河北) 如图，点O为 $\text{[math]}$ 中点，分别延长 $\text{[math]}$ 到点C， $\text{[math]}$ 到点D，使 $\text{[math]}$ ．以点O为圆心，分别以 $\text{[math]}$ ， $\text{[math]}$ 为半径在 $\text{[math]}$ 上方作两个半圆．点P为小半圆上任一点（不与点A，B重合），连接 $\text{[math]}$ 并延长交大半圆于点E，连接 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1） ①求证： $\text{[math]}$ ；
  ②写出∠1，∠2和 $\text{[math]}$ 三者间的数量关系，并说明理由．
2. （2）若 $\text{[math]}$ ，当 $\text{[math]}$ 最大时，直接指出 $\text{[math]}$ 与小半圆的位置关系，并求此时 $\text{[math]}$ （答案保留 $\text{[math]}$ ）．
答案解析收藏纠错 + 选题
26. (2021九上·古冶期中) 如图， $\text{[math]}$ 的半径为6，将该圆周12等分后得到表盘模型，其中整钟点为 $\text{[math]}$ （ $\text{[math]}$ 为1~12的整数），过点 $\text{[math]}$ 作 $\text{[math]}$ 的切线交 $\text{[math]}$ 延长线于点 $\text{[math]}$ ．
1. （1）通过计算比较直径和劣弧 $\text{[math]}$ 长度哪个更长；
2. （2）连接 $\text{[math]}$ ，则 $\text{[math]}$ 和 $\text{[math]}$ 有什么特殊位置关系？请简要说明理由；
3. （3）求切线长 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
27. (2021·河北) 在一平面内，线段 $\text{[math]}$ ，线段 $\text{[math]}$ ，将这四条线段顺次首尾相接．把 $\text{[math]}$ 固定，让 $\text{[math]}$ 绕点 $\text{[math]}$ 从 $\text{[math]}$ 开始逆时针旋转角 $\text{[math]}$ 到某一位置时， $\text{[math]}$ ， $\text{[math]}$ 将会跟随出现到相应的位置．
1. （1）论证如图1，当 $\text{[math]}$ 时，设 $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ，求证： $\text{[math]}$ ；
2. （2）发现当旋转角 $\text{[math]}$ 时， $\text{[math]}$ 的度数可能是多少？
3. （3）尝试取线段 $\text{[math]}$ 的中点 $\text{[math]}$ ，当点 $\text{[math]}$ 与点 $\text{[math]}$ 距离最大时，求点 $\text{[math]}$ 到 $\text{[math]}$ 的距离；
4. （4）拓展 ①如图2，设点 $\text{[math]}$ 与 $\text{[math]}$ 的距离为 $\text{[math]}$ ，若 $\text{[math]}$ 的平分线所在直线交 $\text{[math]}$ 于点 $\text{[math]}$ ，直接写出 $\text{[math]}$ 的长（用含 $\text{[math]}$ 的式子表示）；
  ②当点 $\text{[math]}$ 在 $\text{[math]}$ 下方，且 $\text{[math]}$ 与 $\text{[math]}$ 垂直时，直接写出 $\text{[math]}$ 的余弦值．
答案解析收藏纠错 + 选题