浙教版数学八上第1章三角形的初步知识优生综合题特训-在线组卷

1. (2021七下·宛城期末) 如图， $\text{[math]}$ 为 $\text{[math]}$ 的高， $\text{[math]}$ 、 $\text{[math]}$ 为 $\text{[math]}$ 的角平分线，若 $\text{[math]}$ ， $\text{[math]}$ .

（1） $\text{[math]}$ $\text{[math]}$ ；
（2）求 $\text{[math]}$ 的度数；
（3）若点 $\text{[math]}$ 为线段 $\text{[math]}$ 上任意一点，当 $\text{[math]}$ 为直角三角形时，直接写出 $\text{[math]}$ 的度数.

答案解析收藏纠错 + 选题

2. (2024七下·广州月考) 已知直线 $\text{[math]}$ 与直线 $\text{[math]}$ 、 $\text{[math]}$ 分别交于 $\text{[math]}$ 、 $\text{[math]}$ 两点， $\text{[math]}$ 和 $\text{[math]}$ 的角平分线交于点 $\text{[math]}$ ，且 $\text{[math]}$ .

（1）求证： $\text{[math]}$ ；
（2）如图， $\text{[math]}$ 和 $\text{[math]}$ 的角平分线交于点 $\text{[math]}$ ，求 $\text{[math]}$ 的度数；
（3）如图，若 $\text{[math]}$ ，延长线段 $\text{[math]}$ 得射线 $\text{[math]}$ ，延长线段 $\text{[math]}$ 得射线 $\text{[math]}$ ，射线 $\text{[math]}$ 绕点 $\text{[math]}$ 以每秒15°的速度逆时针旋转360°后停止，射线 $\text{[math]}$ 绕点 $\text{[math]}$ 以每秒3°的速度顺时针旋转180°以后停止.设它们同时旋转 $\text{[math]}$ 秒，问 $\text{[math]}$ 为多少时，射线 $\text{[math]}$ ，直接写出 $\text{[math]}$ 的值 $\text{[math]}$ 秒.

答案解析收藏纠错 + 选题

3. (2021七下·定陶期末)

（1）如图①，在△ABC中，AD，AE分别是△ABC的高和角平分线，若∠B＝30°，∠C＝50°.求∠DAE的度数；
（2）如图②，已知AF平分∠BAC，交边BC于点E，延长AE至点F，过点F作FD⊥BC于点D，若∠B＝x°，∠C＝（x＋36）°.
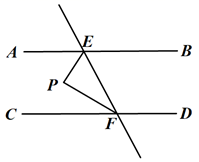
①∠CAE＝ ▲ （含x的代数式表示）；

②求∠F的度数．

答案解析收藏纠错 + 选题

4. 判断下列命题是真命题还是假命题，如果是假命题，举出一个反例．

（1）等角的余角相等；
（2）平行线的同旁内角的平分线互相垂直；
（3）和为180°的两个角叫做邻补角．

答案解析收藏纠错 + 选题

5. (2021八上·临洮期中) AB和AC 相交于点A，BD和CD相交于点D，探究∠BDC与∠B 、 ∠C、∠BAC的关系

小明是这样做的：

解：如图（2）以点A为端点作射线AD

∵∠1是△ABD的外角

∴∠1= ∠B+∠BAD

同理∠2=∠C+∠CAD

∴∠1+∠2=∠B+∠BAD+∠C+∠CAD

即∠BDC=∠B+∠C+∠BAC

小英的思路是：如图（3）延长BD交AC于点E.

（1）按小英的思路完成∠BDC=∠B+∠C+∠BAC这一结论.
（2）如图：△ABC中，BO、CO分别是∠ABC与∠ACB的角平分线，且BO、CO相交于点O.猜想∠BOC与∠A有怎样的关系，并加以证明.

答案解析收藏纠错 + 选题

6. (2021八上·嘉祥月考) 如图1，线段AB、CD相交于点О，连接AD、CB，我们把形如图1的图形称之为“8字形”。如图2，在图1的条件下，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N．试解答下列问题：

（1）在图1中，请直接写出∠A、∠B、∠C、∠D之间的数量关系：
（2）仔细观察，在图2中“8字形”的个数个；
（3）在图2中，若∠D=40°，∠B=36°，试求∠P的度数；
（4）如果图2中∠D和∠B为任意角，其他条件不变，试问∠P与∠D，∠B之间存在着怎样的数量关系(直接写出结论即可)

答案解析收藏纠错 + 选题

7. (2021八上·北京开学考) 已知如图①， $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ 的外角 $\text{[math]}$ 、 $\text{[math]}$ 的角平分线， $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ 、 $\text{[math]}$ 的角平分线， $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ 、 $\text{[math]}$ 的角平分线， $\text{[math]}$ ．

（1）当 $\text{[math]}$ 时， $\text{[math]}$ °， $\text{[math]}$ °；
（2）当 $\text{[math]}$ °时， $\text{[math]}$ ；
（3）如图②，当 $\text{[math]}$ 时， $\text{[math]}$ 、 $\text{[math]}$ 所在直线交于点O，求 $\text{[math]}$ 的度数；
（4）在 $\text{[math]}$ 的条件下，直接写出 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三角之间的数量关系：．

答案解析收藏纠错 + 选题

8. (2024七下·恩施期中) 已知：直线EF分别与直线AB，CD相交于点G，H，并且∠AGE+∠DHE＝180°．

（1）如图1，求证：AB∥CD；
（2）如图2，点M在直线AB，CD之间，连接GM，HM，求证：∠M＝∠AGM+∠CHM；
（3）如图3，在（2）的条件下，射线GH是∠BGM的平分线，在MH的延长线上取点N，连接GN，若∠N＝∠AGM，∠M＝∠N+ $\text{[math]}$ ∠FGN，求∠MHG的度数．

答案解析收藏纠错 + 选题

9. (2021七下·仪征期末) 已知：DE $\text{[math]}$ PQ，点A在直线DE上，点B、C都在PQ上（点B在点C的左侧），连接AB，AC，AB平分∠CAD.

（1）如图1，求证：∠ABC＝∠BAC；
（2）如图2，点K为AB上一点，连接CK，若CK⊥AB，判断∠EAC与∠ACK之间的数量关系，并说明理由；
（3）在（2）的条件下，在直线DE上取一点F，连接FK，使得∠AKF＝30°.若∠DAB＝∠AFK+∠KCB，求∠ACB的度数.（要求：在备用图中画出图形后，再计算）

答案解析收藏纠错 + 选题

10. (2021七下·江都期末) 直线m与直线n相交于C，点A是直线m上一点，点B是直线n上一点， $\text{[math]}$ 的平分线 $\text{[math]}$ 与 $\text{[math]}$ 的平分线 $\text{[math]}$ 的反向延长线相交于点P.

\

（1）如图1，若 $\text{[math]}$ ，则 $\text{[math]}$ ；若 $\text{[math]}$ ，则 $\text{[math]}$ （结果用含 $\text{[math]}$ 的代数式表示）；
（2）如图2，点F是直线n上一点，若点B在点C左侧，点F在点C右侧时，连接 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 的平分线相交于点Q.
①随着点B、F的运动， $\text{[math]}$ 的值是否变化？若发生变化，请说明理由；若不发生变化，试求出其值；

②延长 $\text{[math]}$ 交直线n于点G，作 $\text{[math]}$ 交 $\text{[math]}$ 于点H，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题

11. (2021七下·鼓楼期末) 互动学习课堂上某小组同学对一个课题展开了探究.

小亮：已知，如图三角形 $\text{[math]}$ ，点 $\text{[math]}$ 是三角形 $\text{[math]}$ 内一点，连接 $\text{[math]}$ ， $\text{[math]}$ ，试探究 $\text{[math]}$ 与 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的关系.

小明：可以用三角形内角和定理去解决.

小丽：用外角的相关结论也能解决.

（1）请你在横线上补全小明的探究过程：
∵ $\text{[math]}$ ，（）

∴ $\text{[math]}$ ，（等式性质）

∵ $\text{[math]}$ ，

∴ $\text{[math]}$ ，

∴ $\text{[math]}$ .（）
（2）请你按照小丽的思路完成探究过程；
（3）利用探究的结果，解决下列问题：
①如图①，在凹四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ ▲ ；

②如图②，在凹四边形 $\text{[math]}$ 中， $\text{[math]}$ 与 $\text{[math]}$ 的角平分线交于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ▲ ；

③如图③， $\text{[math]}$ ， $\text{[math]}$ 的十等分线相交于点、 $\text{[math]}$ 、 $\text{[math]}$ 、…、 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为 ▲ ；

④如图④， $\text{[math]}$ ， $\text{[math]}$ 的角平分线交于点 $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系是 ▲ ；

⑤如图⑤， $\text{[math]}$ ， $\text{[math]}$ 的角平分线交于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数.

答案解析收藏纠错 + 选题

12. (2021八上·沭阳月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ cm， $\text{[math]}$ ， $\text{[math]}$ cm，点F从点B出发，沿线段 $\text{[math]}$ 以4cm/s的速度连续做往返运动，点E从点A出发沿线段 $\text{[math]}$ 以2cm/s的速度运动至点G，E、F两点同时出发，当点E到达点G时，E、F两点同时停止运动， $\text{[math]}$ 与 $\text{[math]}$ 交于点D，设点E的运动时间为t（秒）

（1）分别写出当 $\text{[math]}$ 和 $\text{[math]}$ 时线段 $\text{[math]}$ 的长度（用含t的代数式表示）
（2）当 $\text{[math]}$ 时，求t的值；
（3）当 $\text{[math]}$ 时，直接写出所有满足条件的 $\text{[math]}$ 值.

答案解析收藏纠错 + 选题

13. (2020八上·武汉月考) 如图，已知：AB∥CD，E是BD上一点，

（1） AE，CE分别是∠BAC与∠ACD的平分线，求证：AE⊥CE；
（2）若AB+CD=AC，且E是BD中点.求证：CE平分∠ACD.

答案解析收藏纠错 + 选题

14. (2020八上·武汉月考) 在△ABC中，∠ABC=60°，AD，CE分别平分∠CAB，∠ACB，AD与CE交于点O

求证：

（1） ∠AOE=60°；
（2） AC=AE+CD.

答案解析收藏纠错 + 选题

15. (2020八上·巴南月考)

（1）问题背景：
如图 1，在四边形 ABCD 中，AB = AD，∠BAD= 120°，∠B =∠ADC= 90°，E，F 分别是 BC， CD 上的点，且∠EAF = 60°，探究图中线段BE，EF，FD之间的数量关系.

小明同学探究此问题的方法是延长FD到点G，使DG=BE，连结AG，先证明Δ $\text{[math]}$ ΔADG，再证明Δ $\text{[math]}$ ΔAGF，可得出结论，他的结论应是.
（2）探索延伸：
如图 2，在四边形ABCD 中，AB=AD，∠B+∠D=180°，E，F分别是BC，CD上的点，∠EAF= $\text{[math]}$ ∠BAD，上述结论是否依然成立？并说明理由.

答案解析收藏纠错 + 选题

16. (2021七下·沈河期末) 已知：如图1，在 $\text{[math]}$ 和 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .

（1）请说明 $\text{[math]}$ .
（2）如图2，连接 $\text{[math]}$ 和 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 分别交于点 $\text{[math]}$ 和 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数.
（3）在（2）的条件下，若 $\text{[math]}$ ，请直接写出 $\text{[math]}$ 的度数.

答案解析收藏纠错 + 选题

17. (2020七下·长沙期末) 已知： $\text{[math]}$ 的高 $\text{[math]}$ 所在直线与高 $\text{[math]}$ 所在直线相交于点F．

（1）如图1，若 $\text{[math]}$ 为锐角三角形，且 $\text{[math]}$ ， $\text{[math]}$ ，过点F作 $\text{[math]}$ ，交直线 $\text{[math]}$ 于点G，请直接写出 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间的数量关系：；
（2）如图2，若 $\text{[math]}$ ，过点F作 $\text{[math]}$ ，交直线 $\text{[math]}$ 于点G，探究 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间满足的数量关系并加以证明；
（3）在（2）的条件下，将一个 $\text{[math]}$ 角的顶点与点B重合并绕点B旋转，这个角的两边分别交线段 $\text{[math]}$ 于M、N两点（如图3），连接 $\text{[math]}$ ，线段 $\text{[math]}$ 分别与线段 $\text{[math]}$ 、线段 $\text{[math]}$ 、线段 $\text{[math]}$ 相交于P、Q、H三点．
①探究 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间数量关系并加以证明；

②求证： $\text{[math]}$ ．

答案解析收藏纠错 + 选题

18. (2020九下·青县开学考) 已知：在Rt△ABC中，∠ACB=90°，AC=BC ， D是线段AB上一点，连结CD ，将线段CD绕点C逆时针旋转90°得到线段CE ，连结DE ， BE ．

（1）依题意补全图形；
（2）若∠ACD=α，用含α的代数式表示∠DEB；
（3）若△ACD的外心在三角形的内部，请直接写出α的取值范围．

答案解析收藏纠错 + 选题

19. (2019八上·北京期中) 我们知道：有两条边相等的三角形叫做等腰三角形．类似地，我们定义：至少有一组对边相等的四边形叫做等对边四边形．

（1）如图，在 $\text{[math]}$ 中，点 $\text{[math]}$ ， $\text{[math]}$ 分别在 $\text{[math]}$ ， $\text{[math]}$ 上，设 $\text{[math]}$ ， $\text{[math]}$ 相交于点 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ．请你写出图中一个与 $\text{[math]}$ 相等的角，并猜想图中哪个四边形是等对边四边形？
（2）在 $\text{[math]}$ 中，如果 $\text{[math]}$ 是不等于 $\text{[math]}$ 的锐角，点 $\text{[math]}$ ， $\text{[math]}$ 分别在 $\text{[math]}$ ， $\text{[math]}$ 上，且 $\text{[math]}$ ．探究：满足上述条件的图形中是否存在等对边四边形，并证明你的结论．

答案解析收藏纠错 + 选题

20. (2021八上·乾安期中) 如图（1），AB＝4cm，AC⊥AB，BD⊥AB，AC＝BD＝3cm．点P在线段AB上以1cm/s的速度由点A向点B运动，同时，点Q在线段BD上由点B向点D运动．它们运动的时间为t（s）．

（1）若点Q的运动速度与点P的运动速度相等，当t＝1时，△ACP与△BPQ是否全等，请说明理由，并判断此时线段PC和线段PQ的关系；
（2）如图（2），将图（1）中的“AC⊥AB，BD⊥AB”为改“∠CAB＝∠DBA＝60°”，其他条件不变．设点Q的运动速度为xcm/s，是否存在实数x，使得△ACP与△BPQ全等？若存在，求出相应的x、t的值；若不存在，请说明理由.

答案解析收藏纠错 + 选题

21. (2021八上·绍兴开学考) 已知：在△ABC中，BD是边AC的高，BE为∠CBD的角平分线，且AD＝DE ． AO为△ABC的中线，延长AO到点F ．使得BF∥AC ．连接EF ． EF交BC于点G ． AF交BE于点H ．

（1）求证：BF＝CD+DE；
（2）求证：∠FBE＝∠BAC
（3）若∠C＝45°．求证：BD＝BG ．

答案解析收藏纠错 + 选题

22. (2021七下·苏州期末) 探索角的平分线的画法.

（1）画法1：利用直尺和圆规
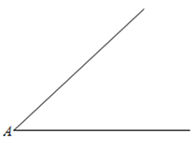
请在图中用直尺和圆规画出 $\text{[math]}$ 的平分线 $\text{[math]}$ ；（不写画法不需证明，保留作图痕迹）
（2）画法2：利用等宽直尺.
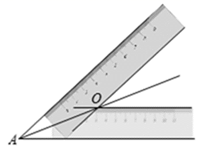
如图，将一把等宽直尺的一边依次落在 $\text{[math]}$ 的两条边上，再过另一边分别画直线，两条直线相交于点O.画射线 $\text{[math]}$ ，则射线 $\text{[math]}$ 是 $\text{[math]}$ 的平分线.这种角的平分线的画法依据的是______.

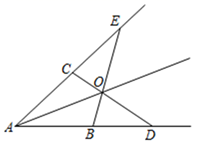
A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$
（3）画法3：利用刻度尺
已知：如图，在 $\text{[math]}$ 的两条边上分别画 $\text{[math]}$ ， $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ ，交点为点O，画射线 $\text{[math]}$ .

求证： $\text{[math]}$ 是 $\text{[math]}$ 的平分线.
（4）画法4：利用你手里带有刻度的一块直角三角尺，设计一种与上述画法不同的角的平分线的画法.请在图中画出 $\text{[math]}$ 的平分线 $\text{[math]}$ ，写出画法，并加以证明.

答案解析收藏纠错 + 选题

23. (2020九上·白云期末) 如图

（1）作图：如图，已知△ABC ， ∠ACB＜120°，
①作等边△ACD ，使得点D ， B分别是直线AC异侧的两个点；

②作等边△BCE ，使得点E ， A分别是直线BC异侧的两个点；

（要求尺规作图，保留作图痕迹，不写作法．）
（2）推理：在（1）所作的图中，设直线BD ， AE的交点为P ，连接PC ，
①求∠APD的度数；

②猜想PA ， PB ， PC与AE之间的等量关系，并证明：
（3）变式：已知△ABC ， ∠ACB＞120°，按（1）的方法作图后，设直线BD ， AE的交点为P ，连接PC ．测得∠PAB＝15°，PA＝ $\text{[math]}$ ，PB＝ $\text{[math]}$ ，PC＝ $\text{[math]}$ ．求点D到直线AB的距离．

答案解析收藏纠错 + 选题

小学

初中

高中

浙教版数学八上第1章三角形的初步知识优生综合题特训

副标题：

*注意事项：

浙教版数学八上第1章三角形的初步知识优生综合题特训

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析

小学

初中

高中

浙教版数学八上第1章 三角形的初步知识优生综合题特训

副标题：

*注意事项：

浙教版数学八上第1章 三角形的初步知识优生综合题特训

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析

浙教版数学八上第1章三角形的初步知识优生综合题特训

浙教版数学八上第1章三角形的初步知识优生综合题特训