




观察下面的解答过程,补充必要的依据或结论.
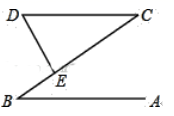
解∵∠1=60°(已知)
∠ABC=∠1 (① ▲ )
∴∠ABC=60°(等量代换)
又∵∠2=120°(已知)
∴(② ▲ )+∠2=180°(等式的性质)
∴AB∥CD (③ ▲ )
又∵∠2+∠BCD=(④ ▲ °)
∴∠BCD=60°(等式的性质)
∵∠D=60°(已知)
∴∠BCD=∠D (⑤ ▲ )
∴BC∥DE (⑥ ▲ )
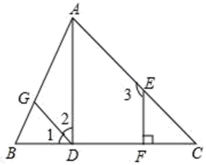
解:∵∠1=∠C,(已知)
∴GD∥ ▲ . ( )
∴∠2=∠DAC.( )
∵∠2+∠3=180°,(已知)
∴∠DAC+∠3=180°.(等量代换)
∴AD∥EF.( )
∴∠ADC=∠ ▲ . ( )
∵EF⊥BC,(已知)
∴∠EFC=90°.( )
∴∠ADC=90°.(等量代换)
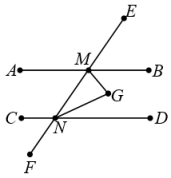
完成下面的证明:
∵MG平分∠BMN,
∴∠GMN=∠BMN( ▲ ),
同理∠GNM=∠DNM.
∵ABCD
∴∠BMN+∠DNM= ▲ ( ▲ ).
∴∠GMN+∠GNM= ▲ .
∵∠GMN+∠GNM+∠G= ▲ ,
∴∠G= ▲ .