
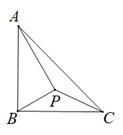



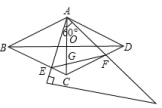

①当点 在线段
上时,若
是以
为腰的等腰三角形,请求出所有符合条件的
的长.
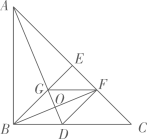
②设 交直线
于点
,连结
,
,若
,则
的长为多少?(直接写出结果).

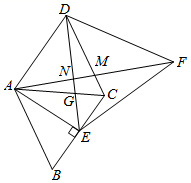
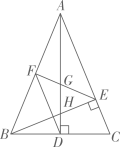
①如图2,若点F落在AC边上,求DG的长.
②是否存在点D,使得△DFG是直角三角形?若存在,求AD的长;若不存在,试说明理由.

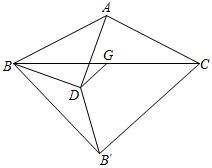
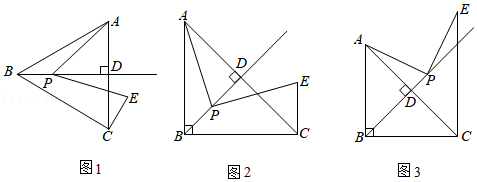
①AC与BD之间的数量关系为;
②∠AMB的度数为;


② 如图3,当点 关于
的对称点
落在直线
上时,求
的值.
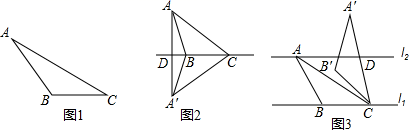
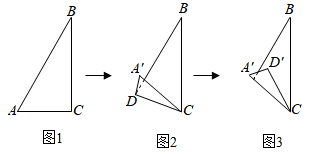
如图1,在△ABC中,AC=6,DC=3,∠ACB=30°,试判断△ABC是否是“等高底”三角形.(填“是”或“否”)
如图2,△ABC是“等高底”三角形,BC是“等底”,作△ABC关于BC所在直线的对称图形得到△A'BC,连接AA'交直线BC于点D.若点B是△AA′C的重心,求 的值.
如图3,已知l1∥l2 , l1与l2之间的距离为2,“等高底”△ABC的“等底”BC在直线l1上,点A在直线l2上,有一边的长是BC的 倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B′C,A′C所在直线交l2于点D,直接写出CD的值.