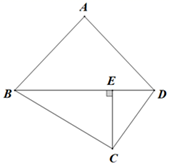
 B .
B .  C .
C .  D .
D . 



 B .
B .  C .
C .  D .
D . 

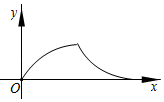
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| h | 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
下列结论:①足球距离地面的最大高度超过20m;②足球飞行路线的对称轴是直线t= ;③点(9,0)在该抛物线上;④足球被踢出5s~7s时,距离地面的高度逐渐下降.其中正确的结论是( )
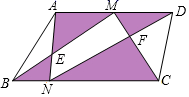
 B .
B . 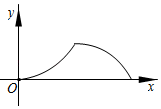 C .
C . 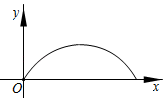 D .
D . 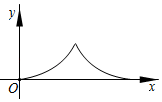



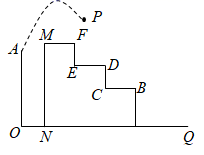


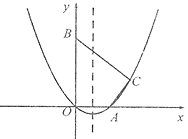
(I)求抛物线的解析式及它的对称轴;
(Ⅱ)点 在线段OB上,点Q在线段BC上,若
,且
,求n的值;
(Ⅲ)在抛物线的对称轴上,是否存在点M,使以A,B,M为顶点的三角形是等腰三形?若存在,求出点M的坐标;若不存在,请说明理由.
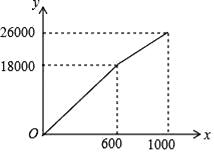


如图,在平面直角坐标系中,将抛物线y=x2先向右平移1个单位,再向下平移
个单位,得到新的抛物线y=ax2+bx+c,该抛物线与y轴交于点B,与x轴正半轴交于点C.
(1)求点B和点C的坐标;
(2)如图1,有一条与y轴重合的直线l向右匀速平移,移动的速度为每秒1个单位,移动的时间为t秒,直线l与抛物线y=ax2+bx+c交于点P,当点P在x轴上方时,求出使△PBC的面积为2的t值;
(3)如图2,将直线BC绕点B逆时针旋转,与x轴交于点M(1,0),与抛物线y=ax2+bx+c交于点A,在y轴上有一点D(0,),在x轴上另取两点E,F(点E在点F的左侧),EF=2,线段EF在x轴上平移,当四边形ADEF的周长最小时,先简单描述如何确定此时点E的位置?再直接写出点E的坐标.

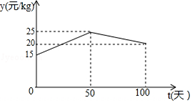
①分别求出当 和
时,
与
的函数关系式;
②设将这批淡水鱼放养 天后一次性出售所得利润为
元,求当
为何值时,
最大?并求出最大值.(利润
销售总额-总成本)
如图,在平面直角坐标系中,抛物线y=ax2+x+c(a≠0)与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,点A的坐标为(4,0),抛物线的对称轴是直线x=
.
