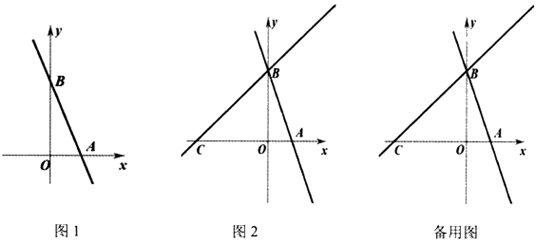
B .
B .  C .
C .  D .
D . 

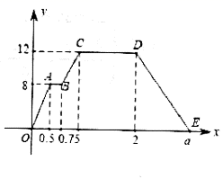
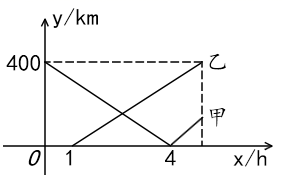
①某小区离小明家12千米;②小明前往某小区时,中途休息了0.25小时;
③小明前往某小区时的平均速度是16千米/小时;
④小明在某小区志愿服务的时间为1小时;⑤a的值为 .
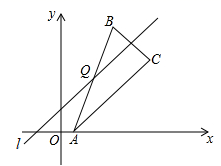

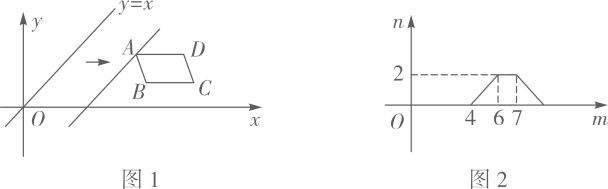




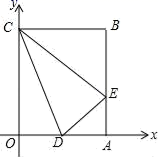
( 1 )在第一象限内画出平行四边形 ;
( 2 )画出点 关于
的对称点
;
( 3 )过点 画出一条直线
,使它平分平行四边形
的周长,请直接写出直线
的解析式;
( 4 )设过点 的直线
的解析式为
,当直线
与平行四边形
有公共点,且直线
不与
轴平行时,请直接写出
的取值范围.