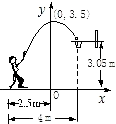
B .
B .  C .
C .  D .
D . 





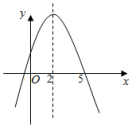

①构造函数,画出图象:根据不等式特征构造二次函数y= ;并在下面的坐标系中(图1)画出二次函数y=
的图象(只画出大致图象即可);
②求得界点,标示所需:当 时,求得方程
的解为;并用虚线标示出函数y=
图象中
<0的部分;
③借助图象,写出解集:由所标示图象,可得不等式 <0的解集为.

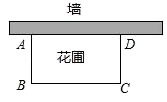

②设P、C之间的距离为y,则y与t满足关系(填“正比例函数”、“一次函数”或“二次函数”);
①求S的表达式(用含t的式子表示);
②求当t为何值时,S取得最大值,这个最大值是多少?

|
销售单价x(元/千克) |
40 |
50 |
|
周销售量y(千克) |
180 |
160 |
|
周销售利润w(元) |
1800 |
3200 |