浙江省历年（2018-2022年）真题分类汇编专题47 解直...

更新时间：2022-10-11 浏览次数：91 类型：二轮复习

一、单选题

1. (2020·嘉兴·舟山) 如图，正三角形ABC的边长为3，将△ABC绕它的外心Ｏ逆时针旋转60°得到△A'B'C'，则它们重叠部分的面积是（）

A . 2 $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020·嘉兴·舟山) 已知二次函数y=x²，当a≤x≤b时m≤y≤n，则下列说法正确的是（）

A . 当n-m=1时，b-a有最小值 B . 当n-m=1时，b-a有最大值 C . 当b-a=1时，n-m无最小值 D . 当b-a=1时，n-m有最大值

答案解析收藏纠错 + 选题
3. 如图，将长、宽分别为12cm，3cm的长方形纸片分别沿AB，AC折叠，点M，N恰好重合于点P.若∠α＝60°，则折叠后的图案（阴影部分）面积为（）

A . （36 $\text{[math]}$ ）cm² B . （36 $\text{[math]}$ ）cm² C . 24cm² D . 36cm²

答案解析收藏纠错 + 选题
4. (2022·冠县模拟) 图1是第七届国际数学教育大会（ICME）的会徽，在其主体图案中选择两个相邻的直角三角形，恰好能组合得到如图2所示的四边形 $\text{[math]}$ .若 $\text{[math]}$ . $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022九上·广宗期末) 如图是一架人字梯，已知 $\text{[math]}$ 米，AC与地面BC的夹角为 $\text{[math]}$ ，则两梯脚之间的距离BC为（）

A . $\text{[math]}$ 米 B . $\text{[math]}$ 米 C . $\text{[math]}$ 米 D . $\text{[math]}$ 米

答案解析收藏纠错 + 选题
6. (2021·湖州) 如图，已知在矩形ABCD中，AB=1，BC= $\text{[math]}$ ，点P是AD边上的一个动点，连结BP，点C关于直线BP的对称点为C₁ ，当点P运动时，点C₁页随之运动。若点P从点A运动到点D，则线段CC₁扫过的区域面积是

A . π B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023·德城模拟) 如图，已知△ABC内接于半径为1的⊙O，∠BAC=θ（θ是锐角），则△ABC的面积的最大值为（）

A . cosθ(1+cosθ) B . cosθ(1+sinθ) C . sinθ(1+sinθ) D . sinθ(1+cosθ)

答案解析收藏纠错 + 选题

二、填空题

8. (2020·金华·丽水) 如图是小明画的卡通图形，每个正六边形的边长都相等，相邻两正六边形的边重合，点A，B，C均为正六边形的顶点，AB与地面BC所成的锐角为β，则tanβ的值是.

答案解析收藏纠错 + 选题
9. (2021·衢州) 图1是某折叠式靠背椅实物图，图2是椅子打开时的侧面示意图，椅面CE与地面平行，支撑杆AD，BC可绕连接点O转动，且 $\text{[math]}$ ，椅面底部有一根可以绕点H转动的连杆HD，点H是CD的中点，FA，EB均与地面垂直，测得 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
1. （1）椅面CE的长度为cm.
2. （2）如图3，椅子折叠时，连杆HD绕着支点H带动支撑杆AD，BC转动合拢，椅面和连杆夹角 $\text{[math]}$ 的度数达到最小值 $\text{[math]}$ 时，A，B两点间的距离为cm（结果精确到0.1cm）.（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）
答案解析收藏纠错 + 选题
10. (2021·绍兴) 图1是一种矩形时钟，图2是时钟示意图，时钟数字2的刻度在矩形ABCD的对角线BD上，时钟中心在矩形ABCD对角线的交点O上.若 $\text{[math]}$ ，则BC长为cm（结果保留根号）.

答案解析收藏纠错 + 选题
11. (2021·湖州) 由沈康身教授所著，数学家吴文俊作序的《数学的魅力》一书中记载了这样一个故事：如图，三姐妹为了平分一块边长为1的祖传正方形地毯，先将地毯分割成七块，再拼成三个小正方形（阴影部分）。则图中AB的长应该是

答案解析收藏纠错 + 选题
12. (2021·绍兴) 已知 $\text{[math]}$ 与 $\text{[math]}$ 在同一平面内，点C，D不重合， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则CD长为.

答案解析收藏纠错 + 选题
13. (2022·温州) 如图是某风车示意图，其相同的四个叶片均匀分布，水平地而上的点M在旋转中心O的正下方。某一时刻，太阳光线恰好垂直照射叶片 OA、OB ，此时各叶片影子在点M右侧成线段 CD ，测得MC=8.5m，CD=13m，垂直于地面的木棒 EF 与影子 FG 的比为2∶3，则点O，M之间的距离等于米．转动时，叶片外端离地面的最大高度等于米．

答案解析收藏纠错 + 选题
14. (2022·金华) 图1是光伏发电场景，其示意图如图2，EF为吸热塔，在地平线EG上的点B，B'处各安装定日镜(介绍见图3).绕各中心点(A，A')旋转镜面，使过中心点的太阳光线经镜面反射后到达吸热器点F处.已知AB=A'B'=1m，EB=8m，EB'=8 $\text{[math]}$ m，在点A观测点F的仰角为45°
1. （1）点F的高度EF为m.
2. （2）设∠DAB=α，∠D'A'B'=β，则α与β的数量关系是.
答案解析收藏纠错 + 选题

三、解答题

15. 图1是放置在水平地面上的落地式话筒架实物图，图2是其示意图.支撑杆AB垂直于地面l，活动杆CD固定在支撑杆上的点E处.若∠AED＝48°，BE＝110cm，DE＝80cm，求活动杆端点D离地面的高度DF.（结果精确到1cm，参考数据：sin48°≈0.74，cos48°≈0.67，tan48°≈1.11）

答案解析收藏纠错 + 选题
16. (2022·台州) 如图1，梯子斜靠在竖直的墙上，其示意图如图2，梯子与地面所成的角α为75° ，梯子AB长3m，求梯子顶部离地竖直高度BC．（结果精确到 0.1m；参考数据：sin75°≈0.97， cos75°≈0.26，tan75°≈3.73）

答案解析收藏纠错 + 选题
17. (2022·湖州) 如图，已知在Rt△ABC中，∠C=90°，AB=5，BC=3．求AC的长和sinA的值．

答案解析收藏纠错 + 选题

四、综合题

18. (2020·嘉兴·舟山) 为了测量一条两岸平行的河流宽度，三个数学研究小组设计了不同的方案，他们在河南岸的点A处测得河北岸的树H恰好在A的正北方向。测量方案与数据如下表：

课题	测量河流宽度
测量工具	测量角度的仪器，皮尺等
测量小组	第一小组	第二小组	第三小组
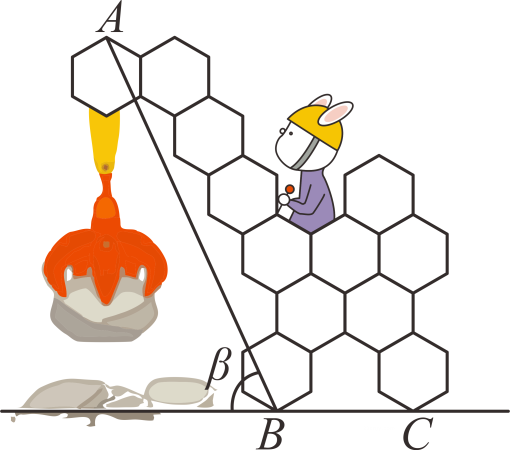
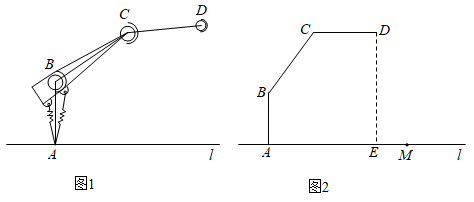
测量方案示意图
说明	点B，C在点A的正东方向	点B，D在点A的正东方向	点B在点A的正东方向，点C在点A的正西方向
测量数据	BC=60m， ∠ABH=70°， ∠ACH=35°	BD=20m， ∠ABH=70°， ∠BCD=35°	BC=101m， ∠ABH=70°， ∠ACH=35°

(参考数据：sin70°≈0.94，sin35°≈0.57，tan70°≈2.75，tan35°≈0.70)

（1）哪个小组的数据无法计算出河宽？
（2）请选择其中一个方案及其数据求出河宽(精确到0.1m)。

答案解析收藏纠错 + 选题

19. (2020·宁波) 图1是一种三角车位锁，其主体部分是由两条长度相等的钢条组成.当位于顶端的小挂锁打开时，钢条可放入底盒中(底盒固定在地面下)，此时汽车可以进入车位；当车位锁上锁后，钢条按图1的方式立在地面上，以阻止底盘高度低于车位锁高度的汽车进入车位.图2是其示意图，经测量，钢条AB=AC=50cm， $\text{[math]}$ .
1. （1）求车位锁的底盒长BC.
2. （2）若一辆汽车的底盘高度为30cm，当车位锁上锁时，问这辆汽车能否进入该车位?
  (参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ )
答案解析收藏纠错 + 选题
20. (2021·路北模拟) 如图，在△ABC中，AB= $\text{[math]}$ ，∠B=45°，∠C=60°.
1. （1）求BC边上的高线长.
2. （2）点E为线段AB的中点，点F在边AC上，连结EF，沿EF将△AEF折叠得到△PEF.
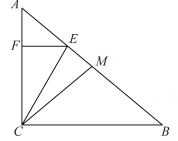
  ①如图2，当点P落在BC上时，求∠AEP的度数.
  
  ②如图3，连结AP，当PF⊥AC时，求AP的长.
答案解析收藏纠错 + 选题
21. 如图，在△ABC中，∠ABC的平分线BD交AC边于点D，AE⊥BC于点E。已知∠ABC=60°，∠C=45°。
1. （1）求证：AB=BD；
2. （2）若AE=3，求△ABC的面积。
答案解析收藏纠错 + 选题
22. (2021·温州) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 是对角线 $\text{[math]}$ 上的两点（点 $\text{[math]}$ 在点 $\text{[math]}$ 左侧），且 $\text{[math]}$ .
1. （1）求证：四边形 $\text{[math]}$ 是平行四边形.
2. （2）当 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 时，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
23. (2024九下·丰城月考) 拓展小组研制的智能操作机器人，如图1，水平操作台为l，底座AB固定，高AB为50cm，连杆BC长度为70cm，手臂CD长度为60cm.点B，C是转动点，且AB，BC与CD始终在同一平面内，
1. （1）转动连杆BC，手臂CD，使 $\text{[math]}$ ， $\text{[math]}$ ，如图2，求手臂端点D离操作台 $\text{[math]}$ 的高度DE的长（精确到1cm，参考数据： $\text{[math]}$ ， $\text{[math]}$ ）.
2. （2）物品在操作台 $\text{[math]}$ 上，距离底座A端110cm的点M处，转动连杆BC，手臂CD，手臂端点D能否碰到点M？请说明理由.
答案解析收藏纠错 + 选题
24. (2021九上·普陀期末) 我国纸伞的制作工艺十分巧妙.如图1，伞不管是张开还是收拢，伞柄 $\text{[math]}$ 始终平分同一平面内两条伞骨所成的角 $\text{[math]}$ ，且 $\text{[math]}$ ，从而保证伞圈D能沿着伞柄滑动.如图2是伞完全收拢时伞骨的示意图，此时伞圈D已滑动到点 $\text{[math]}$ 的位置，且A，B， $\text{[math]}$ 三点共线， $\text{[math]}$ ，B为 $\text{[math]}$ 中点，当 $\text{[math]}$ 时，伞完全张开.
1. （1）求 $\text{[math]}$ 的长.
2. （2）当伞从完全张开到完全收拢，求伞圈D沿着伞柄向下滑动的距离.（参考数据： $\text{[math]}$ ）
答案解析收藏纠错 + 选题
25. (2022·台儿庄模拟) 已知：如图，矩形 $\text{[math]}$ 的对角线 $\text{[math]}$ 相交于点O， $\text{[math]}$ .
1. （1）求矩形对角线的长.
2. （2）过O作 $\text{[math]}$ 于点E，连结BE.记 $\text{[math]}$ ，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
26. (2021·嘉兴) 一酒精消毒瓶如图1，AB为喷嘴，△BCD为按压柄，CE为伸缩连杆，BE和EF为导管，其示意图如图2，∠DBE＝∠BEF＝108°，BD＝6cm ， BE＝4cm ．当按压柄△BCD按压到底时，BD转动到BD′，此时BD′∥EF（如图3）．

（参考数据：sin36°≈0.59，cos36°≈0.81，tan36°≈0.73，sin72°≈0.95，cos72°≈0.31，tan72°≈3.08）
1. （1）求点D转动到点D′的路径长；
2. （2）求点D到直线EF的距离（结果精确到0.1cm）．
答案解析收藏纠错 + 选题
27. (2022·嘉兴) 小华将一张纸对折后做成的纸飞机如图1，纸飞机机尾的横截面是一个轴对称图形，其示意图如图2，已知AD＝BE＝10cm，CD＝CE＝5cm，AD⊥CD，BE⊥CE，∠DCE＝40°．
1. （1）连结DE，求线段DE的长．
2. （2）求点A，B之间的距离．
  （结果精确到0.1cm．参考数据：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36，sin40°≈0.64，cos40°≈0.77，tan40°≈0.84）
答案解析收藏纠错 + 选题
28. (2022·宁波) 每年的11月9日是我国的“全国消防安全教育宣传日”，为了提升全民防灾减灾意识，某消防大队进行了消防演习．如图1，架在消防车上的云梯AB可伸缩（最长可伸至20m），且可绕点B转动，其底部B离地面的距离BC为2m，当云梯顶端A在建筑物EF所在直线上时，底部B到EF的距离BD为9m．

(参考数据：sin53°≈0.8，cos53°≈0.6，tan53°≈1.3)
1. （1）若∠ABD=53°，求此时云梯AB的长．
2. （2）如图2，若在建筑物底部E的正上方19m处突发险情，请问在该消防车不移动位置的前提下，云梯能否伸到险情处？请说明理由．
答案解析收藏纠错 + 选题
29. (2022八上·杭州期中) 如图，在Rt△ACB中，∠ACB=90°，点M为边AB的中点，点E在线段AM上，EF⊥AC于点F，连接CM，CE．已知∠A=50°，∠ACE=30°．
1. （1）求证：CE=CM.
2. （2）若AB=4，求线段FC的长.
答案解析收藏纠错 + 选题
30. (2022·温州) 如图，在△ABC 中， AD⊥BC于点D、E、F分别是AC、AB 的中点，O是 DF 的中点， EO 的延长线交线段 BD 于点G，连结 DE、EF、FG．
1. （1）求证：四边形 DEFG 是平行四边形．
2. （2）当AD=5，tan∠EDC= $\text{[math]}$ =时，求 FG 的长．
答案解析收藏纠错 + 选题
31. (2023·铜仁模拟) 圭表（如图1）是我国古代一种通过测量正午日影长度来推定节气的天文仪器，它包括一根直立的标竿（称为“表”）和一把呈南北方向水平固定摆放的与标竿垂直的长尺（称为“圭”），当正午太阳照射在表上时，日影便会投影在圭面上，圭面上日影长度最长的那一天定为冬至，日影长度最短的那一天定为夏至.图2是一个根据某市地理位置设计的圭表平面示意图，表 AC垂直圭BC，已知该市冬至正午太阳高度角（即∠ABC）为37° ，夏至正午太阳高度角（即∠ADC）为84°，圭面上冬至线与夏至线之间的距离（即DB的长）为4米．
1. （1）求∠BAD的度数．
2. （2）求表AC的长（最后结果精确到0.1米）．
  （参考数据：sin37°≈ $\text{[math]}$ ，cos37°≈ $\text{[math]}$ ，tan37°≈ $\text{[math]}$ ，tan84°≈ $\text{[math]}$ ）
答案解析收藏纠错 + 选题
32. (2022·舟山) 小华将一张纸对折后做成的纸飞机如图1，纸飞机机尾的横截面是一个轴对称图形，其示意图如图2，已知AD=BE=10cm，CD=CE=5cm，AD⊥CD，BE⊥CE，∠DCE=40°．
1. （1）连结DE，求线段DE的长．
2. （2）求点A、B之间的距离．
  (结果精确到0.1cm．参考数据：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36．sin40°≈0.64．cos40°≈0.77，tan40°≈0.84)
答案解析收藏纠错 + 选题
33. (2021·金华) 在平面直角坐标系中，点A的坐标为 $\text{[math]}$ ，点B在直线 $\text{[math]}$ 上，过点B作AB的垂线，过原点O作直线l的垂线，两垂线相交于点C.
1. （1）如图，点B，C分别在第三、二象限内，BC与AO相交于点D.
  ①若 $\text{[math]}$ ，求证： $\text{[math]}$ .
  
  ②若 $\text{[math]}$ ，求四边形 $\text{[math]}$ 的面积.
2. （2）是否存在点B，使得以 $\text{[math]}$ 为顶点的三角形与 $\text{[math]}$ 相似？若存在，求OB的长；若不存在，请说明理由.
答案解析收藏纠错 + 选题
34. (2022·嘉兴) 小东在做九上课本123页习题：“1： $\text{[math]}$ 也是一个很有趣的比．已知线段AB（如图1），用直尺和圆规作AB上的一点P，使AP：AB＝1： $\text{[math]}$ ．”小东的作法是：如图2，以AB为斜边作等腰直角三角形ABC，再以点A为圆心，AC长为半径作弧，交线段AB于点P，点P即为所求作的点．小东称点P为线段AB的“趣点”．
1. （1）你赞同他的作法吗？请说明理由．
2. （2）小东在此基础上进行了如下操作和探究：连结CP，点D为线段AC上的动点，点E在AB的上方，构造△DPE，使得△DPE∽△CPB．
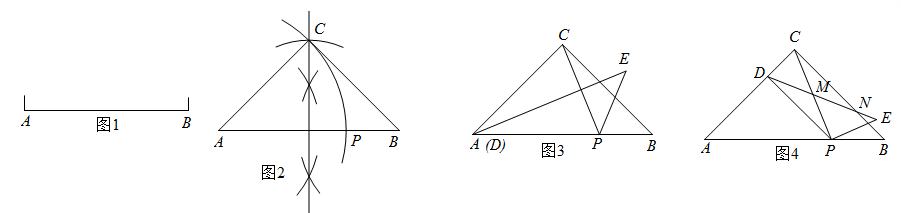
  ①如图3，当点D运动到点A时，求∠CPE的度数．
  
  ②如图4，DE分别交CP，CB于点M，N，当点D为线段AC的“趣点”时（CD＜AD），猜想：点N是否为线段ME的“趣点”？并说明理由．
答案解析收藏纠错 + 选题
35. (2022·温州) 如图1， AB 为半圆O的直径，C为 BA 延长线上一点， CD 切半圆于点D， BE⊥CD ，交 CD 延长线于点E，交半圆于点F，已知BC=5，BE=3．点P，Q分别在线段 AB、BE上（不与端点重合），且满足 $\text{[math]}$ ．设BQ=x，CP=y．
1. （1）求半圆O的半径．
2. （2）求y关于x的函数表达式．
3. （3）如图2，过点P作 PR⊥CE 于点R，连结 PQ、RQ．
  ①当 △PQR 为直角三角形时，求x的值．
  
  ②作点F关于 QR 的对称点 F' ，当点 F'落在 BC上时，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题