备考2023年中考数学杭州卷变式阶梯训练21-23题

更新时间：2022-10-16 浏览次数：325 类型：二轮复习

一、第二十一题

1. (2022八上·杭州期中) 如图，在Rt△ACB中，∠ACB=90°，点M为边AB的中点，点E在线段AM上，EF⊥AC于点F，连接CM，CE．已知∠A=50°，∠ACE=30°．
1. （1）求证：CE=CM.
2. （2）若AB=4，求线段FC的长.
答案解析收藏纠错 + 选题
2. (2022·扬州模拟) 在△ABC中，∠C＝90°.
1. （1）已知c＝8 $\text{[math]}$ ， ∠A＝60°，求∠B，a，b；
2. （2）已知a＝3 $\text{[math]}$ ， ∠A＝45°，求∠B，b，c.
答案解析收藏纠错 + 选题
3. (2022·长宁模拟) 已知：如图，AO是⊙O的半径，AC为⊙O的弦，点F为的中点，OF交AC于点E，AC=10，EF=3·
1. （1）求AO的长；
2. （2）过点C作CD⊥AO，交AO延长线于点D，求OD的长·
答案解析收藏纠错 + 选题
4. (2022·蓝田模拟) 如图，在Rt $\text{[math]}$ ABC中， $\text{[math]}$ ，点O为BC上一点，以O为圆心、OB为半径的⊙ $\text{[math]}$ 切AC于点D，连接OA、BD、OA与BD相交于点E.
1. （1）求证：BD平分 $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ， ⊙ $\text{[math]}$ 的半径为10，求OE的长.
答案解析收藏纠错 + 选题
5. (2022·金乡县模拟) 在 $\text{[math]}$ 中， $\text{[math]}$ ， ∠A，∠B，∠C所对的边分别是a，b，c，利用锐角三角函数定义很容易推导出一些关系式，如 $\text{[math]}$ ， $\text{[math]}$ 等，这些公式在三角函数式子的变形中运用比较广泛．设 $\text{[math]}$ ， $\text{[math]}$ 是锐角，定义：当 $\text{[math]}$ 时，两角和的余弦公式： $\text{[math]}$ ．
例：计算 $\text{[math]}$ 的值．
$\text{[math]}$
$\text{[math]}$ $\text{[math]}$ $\text{[math]}$ ，
两角差的余弦公式： $\text{[math]}$ ．利用类比的方法运用公式求解．
1. （1）计算 $\text{[math]}$ ．
2. （2）计算 $\text{[math]}$ 的值；
3. （3）一副斜边长均为16的三角板拼成如图所示的图形，求过A、B、C、D四点的矩形ABEF的面积．
答案解析收藏纠错 + 选题
6. (2022·莲湖模拟)
1. （1）问题提出：如图1，在 $\text{[math]}$ 中，点 $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ 、 $\text{[math]}$ 的中点，连接 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ ；
2. （2）问题探究：如图2，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 上一点（可与端点重合），连接 $\text{[math]}$ 、 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 面积的最小值；
3. （3）问题解决：某湿地公园拟建一个梯形花园 $\text{[math]}$ ，示意图如图3所示，其中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .管理员计划在 $\text{[math]}$ 区域种植水生植物，在 $\text{[math]}$ 区域种植甲种花卉.根据设计要求，要满足点 $\text{[math]}$ 在 $\text{[math]}$ 上， $\text{[math]}$ ， $\text{[math]}$ 是锐角，且 $\text{[math]}$ ，若种植水生植物每平方米需400元，种植甲种花卉每平方米需100元，求种植水生植物和种植甲种花卉所需总费用至少为多少元？
答案解析收藏纠错 + 选题
7. (2022·梓潼模拟) 如图，矩形ABCD中，AB=6，BC=2 $\text{[math]}$ ，点O是AB的中点，点P在AB的延长线上，且BP=3.一动点E从O点出发，以每秒1个单位长度的速度沿OA匀速运动，到达A点后，立即以原速度沿AO返回；另一动点F从P点发发，以每秒1个单位长度的速度沿射线PA匀速运动，点E、F同时出发，当两点相遇时停止运动，在点E、F的运动过程中，以EF为边作等边△EFG，使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒（t≥0）.
1. （1）当等边△EFG的边FG恰好经过点C时，求运动时间t的值；
2. （2）在整个运动过程中，设等边△EFG和矩形ABCD重叠部分的面积为S，请直接写出S与t之间的函数关系式和相应的自变量t的取值范围；
3. （3）设EG与矩形ABCD的对角线AC的交点为H，是否存在这样的t，使△AOH是等腰三角形？若存大，求出对应的t的值；若不存在，请说明理由.
答案解析收藏纠错 + 选题

二、第二十二题

8. (2022·杭州) 设二次函数y₁=2x²+bx+c(b，c是常数)的图象与x轴交于A，B两点．
1. （1）若A，B两点的坐标分别为(1，0)，(2，0)，求函数y)的表达式及其图象的对称轴．
2. （2）若函数y₁的表达式可以写成心=2(x-h)²-2(h是常数)的形式，求b+c的最小值．
3. （3）设一次函数y₂=x-m(m是常数)，若函数y₁的表达式还可以写成y₁=2(x-m)(x-m-2)的形式，当函数y=y₁-y₂的图象经过点(x₀ ， 0)时，求x₀-m的值．
答案解析收藏纠错 + 选题
9. (2022·萧山模拟) 已知二次函数y＝ax²＋bx－3（a≠0）.
1. （1）若函数图象的对称轴为直线x＝1，且顶点在x轴上，求a的值；
2. （2）若a＝1，b＝2，点（m，n）为该二次函数图象在第三象限内的点，请分别求出m，n的取值范围；
3. （3）若点P（a，a－3）始终是函数图象上的点，求证： $\text{[math]}$ .
答案解析收藏纠错 + 选题
10. (2022·舟山模拟) 如图，在平面直角坐标系中，二次函数y＝ax²+4x﹣3图象的顶点是A，与x轴交于B，C两点，与y轴交于点D.点B的坐标是（1，0）.
1. （1）求A，C两点的坐标，并根据图象直接写出当y＞0时x的取值范围.
2. （2）将图象向上平移m个单位后，二次函数图象与x轴交于E，F两点，若EF＝6，求m的值.
答案解析收藏纠错 + 选题
11. (2022·富阳模拟) 在直角坐标系中，点A(1，m)和点B(3，n)在二次函数 $\text{[math]}$ 的图象上.
1. （1）若 $\text{[math]}$ ， $\text{[math]}$ ，求二次函数的表达式及图象的对称轴.
2. （2）若 $\text{[math]}$ ，试说明二次函数的图象与x轴必有交点.
3. （3）若点C( $\text{[math]}$ ， $\text{[math]}$ )是二次函数图象上的任意一点，且满足 $\text{[math]}$ ，求mn的取值范围.
答案解析收藏纠错 + 选题
12. (2022·新河模拟) 平面直角坐标系 $\text{[math]}$ 中，已知抛物线 $\text{[math]}$ 经过 $\text{[math]}$ ， $\text{[math]}$ 两点，其中 $\text{[math]}$ 为常数．
1. （1）求 $\text{[math]}$ 的值，并用含 $\text{[math]}$ 的代数式表示 $\text{[math]}$ ；
2. （2）若抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴有公共点，求 $\text{[math]}$ 的值；
3. （3）设 $\text{[math]}$ ， $\text{[math]}$ 是抛物线 $\text{[math]}$ 上的两点，请比较 $\text{[math]}$ 与0的大小，并说明理由．
答案解析收藏纠错 + 选题
13. (2022·陈仓模拟) 在平面直角坐标系中，抛物线L：y＝﹣x²+x+2与y轴交于点C，与x轴交于A、B两点（点A在点B的左侧）.
1. （1）求A、B、C三点的坐标；
2. （2）连接AC、BC，以点C为位似中心，将△ABC扩大到原来的2倍得到△A₁B₁C，其中点A₁、B₁分别是点A、B的对应点，如何平移抛物线L才能使其同时经过点A₁、B₁ ，求出所有的平移方式.
答案解析收藏纠错 + 选题
14. (2020九下·南昌月考) 定义：若两条抛物线在x轴上经过两个相同点，那么我们称这两条抛物线是“同交点抛物线”，在x轴上经过的两个相同点称为“同交点”，已知抛物线y=x² +bx+c经过(﹣2，0)、( ﹣4，0)，且一条与它是“同交点抛物线”的抛物线y=ax² +ex+f经过点( ﹣3，3)．
1. （1）求b、c及a的值；
2. （2）已知抛物线y =﹣x² +2x +3与抛物线y_n= $\text{[math]}$ x²﹣ $\text{[math]}$ x﹣n （n为正整数）
  ①抛物线y和抛物线y_n是不是“同交点抛物线”？若是，请求出它们的“同交点”，并写出它们一条相同的图像性质；若不是，请说明理由．
  
  ②当直线y = $\text{[math]}$ x+ m与抛物线y、y_n ，相交共有4个交点时，求m的取值范围．
  
  ③若直线y =k（k <0）与抛物线y =﹣x² +2x +3与抛物线y_n = $\text{[math]}$ x²﹣ $\text{[math]}$ x﹣n （n为正整数）共有4个交点，从左至右依次标记为点A、点B、点C、点D，当AB =BC=CD时，求出k、n之间的关系式
答案解析收藏纠错 + 选题

三、第二十三题

15. (2022·杭州) 在正方形ABCD中，点M是边AB的中点，点E在线段AM上（不与点A重合），点F在边BC上，且AE=2BF，连接EF，以EF为边在正方形ABCD内作正方形EFGH．
1. （1）如图1．若AB=4，当点E与点M重合时，求正方形EFGH的面积
2. （2）如图2．已知直线HG分别与边AD，BC交于点I，J，射线EH与射线AD交于点K．
  ①求证：EK=2EH；
  
  ②设∠AEK=α，△FGJ和四边形AEHI的面积分别为S₁、S₂ ．
  
  求证： $\text{[math]}$ =4sin²α-1．
答案解析收藏纠错 + 选题
16. (2022·阳谷模拟) 如图，点 $\text{[math]}$ ， $\text{[math]}$ 分别在正方形 $\text{[math]}$ 的边 $\text{[math]}$ ， $\text{[math]}$ 上，且 $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ 分别在边 $\text{[math]}$ ， $\text{[math]}$ 上，且 $\text{[math]}$ ，垂足为 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）若正方形 $\text{[math]}$ 边长为5， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长度．
答案解析收藏纠错 + 选题
17. (2022·路桥模拟) 如图，对折正方形纸片 $\text{[math]}$ ，使 $\text{[math]}$ 与 $\text{[math]}$ 重合，折痕为 $\text{[math]}$ .将纸片展平，再进行折叠，使点C落在 $\text{[math]}$ 上的点E处，折痕 $\text{[math]}$ 交 $\text{[math]}$ 于点F.
1. （1）求证： $\text{[math]}$ ；
2. （2）若正方形纸片 $\text{[math]}$ 的边长为3，求折痕 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
18. (2023九上·商河月考) 如图①，四边形 $\text{[math]}$ 是正方形，点E是 $\text{[math]}$ 上一点，连接 $\text{[math]}$ ，以 $\text{[math]}$ 为一边作正方形 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）如图②，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点H，连接 $\text{[math]}$ ，求证： $\text{[math]}$ ；
3. （3）在（2）的条件下，若 $\text{[math]}$ ，点H恰为 $\text{[math]}$ 中点，求 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题
19. (2022九上·杭州月考) 正方形 $\text{[math]}$ 边长为3，点 $\text{[math]}$ 是 $\text{[math]}$ 上一点，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ .
1. （1）如图1，若 $\text{[math]}$ ，求 $\text{[math]}$ 的值；
2. （2）如图1，若 $\text{[math]}$ ，求证：点 $\text{[math]}$ 是 $\text{[math]}$ 的中点；
3. （3）如图2，点 $\text{[math]}$ 为 $\text{[math]}$ 上一点，且满足 $\text{[math]}$ ，设 $\text{[math]}$ ， $\text{[math]}$ ，试探究 $\text{[math]}$ 与 $\text{[math]}$ 的函数关系.
答案解析收藏纠错 + 选题
20. (2022·光明模拟) 如图
如图（1），在Rt△ABC中，∠C＝90°，边AC＝8，BC＝6，点M、N分别在线段AC、BC上，将△ABC沿直线MN翻折，点C的对应点是C′．
1. （1）当M、N分别是所在边的中点时，求线段CC′的长度；
2. （2）若CN＝2，求点C′到线段AB的最短距离；
3. （3）如图（2），当点C′落在边AB上时，
  ①四边形CMC′N能否成为正方形？若能，求出CM的值；若不能，说明理由．
  ②请直接写出点C′运动的路程长度．
答案解析收藏纠错 + 选题
21. (2022·宾阳模拟) 【探索发现】
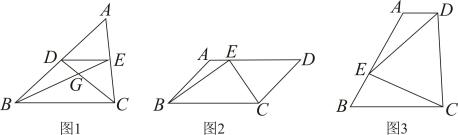
如图①，将△ABC沿中位线EH折叠，使点A的对称点D落在BC边上，再将△BED和△DHC分别沿EF、HG折叠，使点B、C均落在点D处，折痕形成一个四边形EFGH.小刚在探索这个问题时发现四边形EFGH是矩形.

小刚是这样想的：
1. （1）请参考小刚的思路写出证明过程；
2. （2）连接AD，当AD＝BC时，直接写出线段EF，BF，CG的数量关系；
3. （3）【理解运用】
  如图②，在四边形ABCD中，AD∥BC，∠B＝90°，AB＝8，DC＝10，AD＜BC，点E为AB的中点，把四边形ABCD折叠成如图②所示的正方形EFGH，顶点C，D落在点M处，顶点A，B落在点N处，求BC的长.
答案解析收藏纠错 + 选题