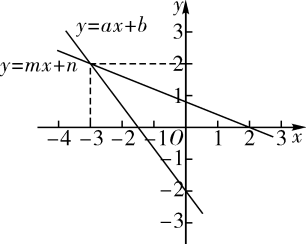
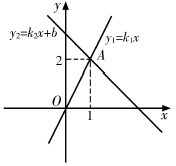
①在一次函数的图象中,
的值随着
值的增大而增大;②方程组
的解为
;③方程
的解为
;④当
时,
.
其中结论正确的个数是( )

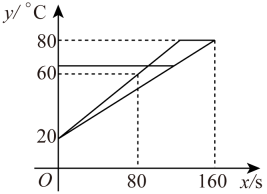
甲:所有商品按原价8.5折出售;
乙:一次购买商品总额不超过300元的按原价付费,超过300元的部分打7折.
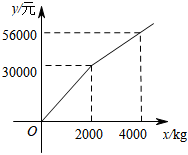
设需要购买体育用品的原价总额为元,去甲商店购买实付
元,去乙商店购买实付
元,其函数图象如图所示.

甲型客车 | 乙型客车 | |
载客量(人/辆) | 35 | 30 |
租金(元/辆) | 400 | 320 |
学校计划此次劳动实践活动的租金总费用不超过3000元.