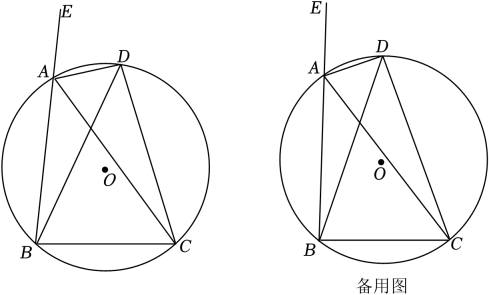
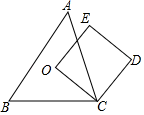

①求证:;
②若 ,
, 求
的半径.
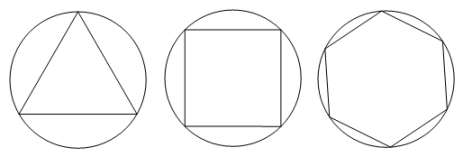
①若 , 则该正n边形的“接近度”等于.
②若 , 则该正n边形的“接近度”等于.
③当“接近度”等于.时,正n边形就成了圆.
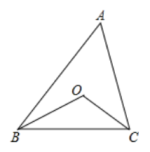
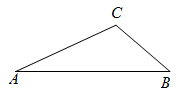
三角形关型 | 直角三角形 | 锐角三角形 | 钝角三角形 |
垂心的位置 | 直角顶点 | ① | 在三角形外部 |
垂心的性质 | 三角形任意顶点到垂心的距离等于外心到对边的距离的两倍. | ||
图形 |
|
| |
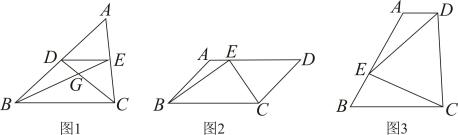
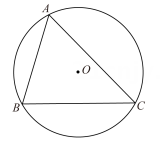
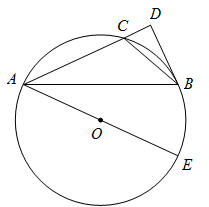
已知:如图1,⊙O是的外接圆,
, H是
的垂心,
, 垂足为E.
求证:.
已知实数m,n满足(2m2+n2+1)(2m2+n2-1)=80,试求2m2+n2的值.
解:设2m2+n2=t,则原方程变为(t+1)(t-1)=80,整理得t2-1=80,t2=81,
所以t=±9,因为2m2+n2≥0,所以2m2+n2=9.
上面这种方法称为“换元法”,把其中某些部分看成一个整体,并用新字母代替(即换元),则能使复杂的问题简单化.
根据以上阅读材料内容,解决下列问题,并写出解答过程.