2023年中考数学精选真题实战测试49 锐角三角函数 A

更新时间：2023-03-01 浏览次数：468 类型：二轮复习

一、单选题（每题3分，共30分）

1. (2023·宽城模拟) 如图，一条河两岸互相平行，为测得此河的宽度PT（PT与河岸PQ垂直），测P、Q两点距离为m米， $\text{[math]}$ ，则河宽PT的长度是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022·长春) 如图是长春市人民大街下穿隧道工程施工现场的一台起重机的示意图，该起重机的变幅索顶端记为点A，变幅索的底端记为点B， $\text{[math]}$ 垂直地面，垂足为点D， $\text{[math]}$ ，垂足为点C．设 $\text{[math]}$ ，下列关系式正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024·柳北模拟) 如图，从热气球A看一栋楼底部C的俯角是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023·会宁模拟) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的高，若 $\text{[math]}$ ， $\text{[math]}$ ，则边 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023九上·聊城月考) 如图，在 $\text{[math]}$ 网格正方形中，每个小正方形的边长为1，顶点为格点，若 $\text{[math]}$ 的顶点均是格点，则 $\text{[math]}$ 的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022·毕节) 如图，某地修建一座高 $\text{[math]}$ 的天桥，已知天桥斜面 $\text{[math]}$ 的坡度为 $\text{[math]}$ ，则斜坡 $\text{[math]}$ 的长度为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023九上·郑州经济技术开发月考) 如图，坡角为α的斜坡上有一棵垂直于水平地面的大树AB，当太阳光线与水平线成45°角沿斜坡照下，在斜坡上的树影BC长为m，则大树AB的高为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2022·广元) 如图，在正方形方格纸中，每个小正方形的边长都相等，A，B，C，D都在格点处，AB与CD相交于点P，则cos∠APC的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023·郧西模拟) 如图，已知点B，D，C在同一直线的水平，在点C处测得建筑物AB的顶端A的仰角为α，在点D处测得建筑物AB的顶端A的仰角为β， $\text{[math]}$ ，则建筑物AB的高度为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023九上·温州月考) 一配电房示意图如图所示，它是一个轴对称图形.已知BC=6m.∠ABC=α.则房顶A离地面EF的高度为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题填空题（每空3分，共18分）

11. (2023·嘉祥模拟) 一艘轮船位于灯塔 $\text{[math]}$ 的南偏东 $\text{[math]}$ 方向，距离灯塔30海里的 $\text{[math]}$ 处，它沿北偏东 $\text{[math]}$ 方向航行一段时间后，到达位于灯塔 $\text{[math]}$ 的北偏东 $\text{[math]}$ 方向上的 $\text{[math]}$ 处，此时与灯塔 $\text{[math]}$ 的距离约为海里．（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
12. (2023·昆明模拟) 某校数学兴趣小组开展无人机测旗杆的活动：已知无人机的飞行高度为30m，当无人机飞行至A处时，观测旗杆顶部的俯角为30°，继续飞行20m到达B处，测得旗杆顶部的俯角为60°，则旗杆的高度约为m．（参考数据： $\text{[math]}$ ，结果按四舍五八保留一位小数）

答案解析收藏纠错 + 选题
13. (2022·西宁) 在Rt△ABC中，∠C=90°，AC=1，BC= $\text{[math]}$ ，则cosA=．

答案解析收藏纠错 + 选题
14. (2022·柳州) 如图，某水库堤坝横断面迎水坡的坡角为 $\text{[math]}$ ， $\text{[math]}$ ，堤坝高 $\text{[math]}$ ，则迎水坡面 $\text{[math]}$ 的长度为 $\text{[math]}$

答案解析收藏纠错 + 选题
15. (2022·通辽) 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ 为 $\text{[math]}$ 上的点， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2022·南通) 如图，点O是正方形 $\text{[math]}$ 的中心， $\text{[math]}$ ． $\text{[math]}$ 中， $\text{[math]}$ 过点D， $\text{[math]}$ 分别交 $\text{[math]}$ 于点G，M，连接 $\text{[math]}$ ．若 $\text{[math]}$ ，则 $\text{[math]}$ 的周长为．

答案解析收藏纠错 + 选题

三、解答题（共10题，共72分）

17. (2022·西藏) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2022·湘西) 计算： $\text{[math]}$ ﹣2tan45°+|﹣3|+（π﹣2022）⁰ ．

答案解析收藏纠错 + 选题
19. (2024九下·金寨期末) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题

20. (2022·枣庄) 为传承运河文明，弘扬民族精神，枣庄市政府重建了台儿庄古城．某校“综合与实践”小组开展了测量台儿庄古城城门楼（如图①）高度的实践活动，请你帮他们完成下面的实践报告．

测量台儿庄古城城门楼高度的实践报告

活动课题	测量台儿庄古城城门楼高度
活动目的	运用三角函数知识解决实际问题
活动工具	测角仪、皮尺等测量工具
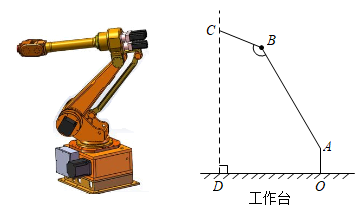
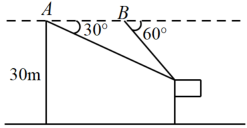
方案示意图		测量步骤	如图② ⑴利用测角仪站在B处测得城门楼最高点P的仰角为39°； ⑵前进了10米到达A处（选择测点A，B与O在同一水平线上，A，B两点之间的距离可直接测得，测角仪高度忽略不计），在A处测得P点的仰角为56°．
参考数据	sin39°≈0.6，cos39°≈0.8，tan39°≈0.8，sin56°≈0.8，cos56°≈0.6，tan56°≈1.5．
计算城门楼PO的高度（结果保留整数）

答案解析收藏纠错 + 选题

21. (2023·深圳模拟) 小明学了《解直角三角形》内容后，对一条东西走向的隧道 $\text{[math]}$ 进行实地测量．如图所示，他在地面上点C处测得隧道一端点A在他的北偏东 $\text{[math]}$ 方向上，他沿西北方向前进 $\text{[math]}$ 米后到达点D，此时测得点A在他的东北方向上，端点B在他的北偏西 $\text{[math]}$ 方向上，（点A、B、C、D在同一平面内）
1. （1）求点D与点A的距离；
2. （2）求隧道 $\text{[math]}$ 的长度．（结果保留根号）
答案解析收藏纠错 + 选题
22. (2022·六盘水) “五一”节期间，许多露营爱好者在我市郊区露营，为遮阳和防雨会搭建一种“天幕”，其截面示意图是轴对称图形，对称轴是垂直于地面的支杆 $\text{[math]}$ ，用绳子拉直 $\text{[math]}$ 后系在树干 $\text{[math]}$ 上的点 $\text{[math]}$ 处，使得 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在一条直线上，通过调节点 $\text{[math]}$ 的高度可控制“天幕”的开合， $\text{[math]}$ m， $\text{[math]}$ m．

（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）
1. （1）天晴时打开“天幕”，若 $\text{[math]}$ ，求遮阳宽度 $\text{[math]}$ （结果精确到0.1m）；
2. （2）下雨时收拢“天幕”， $\text{[math]}$ 从65°减少到45°，求点 $\text{[math]}$ 下降的高度（结果精确到0.1m）．
答案解析收藏纠错 + 选题
23. (2022·安顺) 随着我国科学技术的不断发展，5G移动通信技术日趋完善．某市政府为了实现5G网络全覆盖，2021~2025年拟建设5G基站3000个，如图，在斜坡 $\text{[math]}$ 上有一建成的5G基站塔 $\text{[math]}$ ，小明在坡脚 $\text{[math]}$ 处测得塔顶 $\text{[math]}$ 的仰角为 $\text{[math]}$ ，然后他沿坡面 $\text{[math]}$ 行走了50米到达 $\text{[math]}$ 处， $\text{[math]}$ 处离地平面的距离为30米且在 $\text{[math]}$ 处测得塔顶 $\text{[math]}$ 的仰角 $\text{[math]}$ ．（点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 均在同一平面内， $\text{[math]}$ 为地平线）（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）
1. （1）求坡面 $\text{[math]}$ 的坡度；
2. （2）求基站塔 $\text{[math]}$ 的高．
答案解析收藏纠错 + 选题
24. (2023·合肥模拟) 2022年6月5日，“神舟十四号”载人航天飞船搭载“明星”机械臂成功发射．如图是处于工作状态的某型号手臂机器人示意图， $\text{[math]}$ 是垂直于工作台的移动基座， $\text{[math]}$ 、 $\text{[math]}$ 为机械臂， $\text{[math]}$ m， $\text{[math]}$ m， $\text{[math]}$ m， $\text{[math]}$ ．机械臂端点 $\text{[math]}$ 到工作台的距离 $\text{[math]}$ m．
1. （1）求 $\text{[math]}$ 、 $\text{[math]}$ 两点之间的距离；
2. （2）求 $\text{[math]}$ 长．（结果精确到0.1m，参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）
答案解析收藏纠错 + 选题
25. (2022·攀枝花) 第24届冬奥会（也称2022年北京冬奥会）于2022年2月4日至2月20日在中国北京举行，北京成为了历史上第一座既举办过夏奥会又举办过冬奥会的城市.冬奥会上跳台滑雪是一项极为壮观的运动.运动员经过助滑、起跳、空中飞行和着陆，整个动作连贯一致，一气呵成，如图，某运动员穿着滑雪板，经过助滑后，从倾斜角 $\text{[math]}$ 的跳台A点以速度 $\text{[math]}$ 沿水平方向跳出，若忽略空气阻力影响，水平方向速度将保持不变.同时，由于受重力作用，运动员沿竖直方向会加速下落，因此，运动员在空中飞行的路线是抛物线的一部分，已知该运动员在B点着陆， $\text{[math]}$ ，且 $\text{[math]}$ .忽略空气阻力，请回答下列问题：
1. （1）求该运动员从跳出到着陆垂直下降了多少m？
2. （2）以A为坐标原点建立直角坐标系，求该抛物线表达式；
3. （3）若该运动员在空中共飞行了4s，求他飞行2s后，垂直下降了多少m？
答案解析收藏纠错 + 选题
26. (2024·临沂一模) 知识再现：如图1，在Rt△ABC中，∠C＝90°，∠A，∠B，∠C的对边分别为a，b，c．
∵ $\text{[math]}$ ， $\text{[math]}$

∴ $\text{[math]}$ ， $\text{[math]}$

∴ $\text{[math]}$
1. （1）拓展探究：如图2，在锐角ABC中，∠A，∠B，∠C的对边分别为a，b，c．请探究 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的关系，并写出探究过程．
2. （2）解决问题：如图3，为测量点A到河对岸点B的距离，选取与点A在河岸同一侧的点C，测得AC＝60m，∠A＝75°，∠C＝60°．请用拓展探究中的结论，求点A到点B的距离．
答案解析收藏纠错 + 选题