参考数据:≈1.41,
≈1.73.


结果精确到
,参考数据
,
,



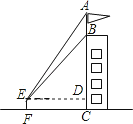
①用含a的代数式表示DQ的长度并求出的值;
②已知对方守门员伸开双臂后,可成功防守的范围为 , 若此时守门员站在张角
内,双臂张开MN垂直于AQ进行防守,求MN中点与AB的距离至少为多少时才能确保防守成功.(结果用含a的代数式表示)
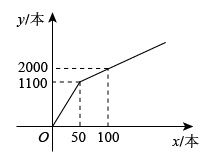
①当时,求出w与x间的函数表达式;
②若购进A种图书不少于60本,且不超过B种图书本数的2倍,那么应该怎样分配购买A,B两种图书才能使总费用最少?最少总费用多少元?
x | 4 | 12 | 16 | 24 | 28 | 36 |
y | 0 | 1 | 1.5 | 2.5 | 3 | 4 |

生产成本(元/件) | 销售单价(元/件) | |
“冰墩墩” | 42 | 50 |
“雪容融” | 35 | 41 |
设该厂每天制作“冰墩墩”挂件x件,每天获得的利润为y元.

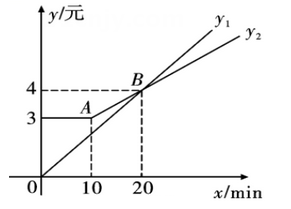
①求 的长度.
② 为边
上一点,以
、
、
中的两点及点
为顶点的三角形为等腰三角形,直接写出
的长度.


(Ⅰ)如图③,当点D在线段AB上运动时,设AD=a,BD=b,求S1S2的表达式(结果用a,b和α的三角函数表示).
(Ⅱ)如图④,当点D在BA的延长线上运动时,设AD=a,BD=b,直接写出S1S2的表达式,不必写出解答过程.

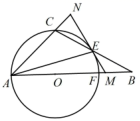
①求y与x的关系式;
②若△DEF的周长为 时,求⊙O的半径.


如图1, 和
均为等边三角形,点A,D,E在同一直线上,连接
.
①线段 ,
之间的数量关系为;
② 的度数为;
如图2, 和
均为等腰直角三角形,
,点B,D,E在同一直线上,连接
,求
的值及
的度数;
如图3,在正方形 中,
,若点P满足
,且
,请直接写出点C到直线
的距离.


①若∠BDE=45°,求PD的长.
②若ΔBED为等腰三角形,求直接写出所有满足条件的BD的长.