|
x(h) |
… |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
… |
|
Y(cm |
… |
189 |
137 |
103 |
80 |
101 |
133 |
202 |
260 |
… |
(数据来自某海洋研究所)
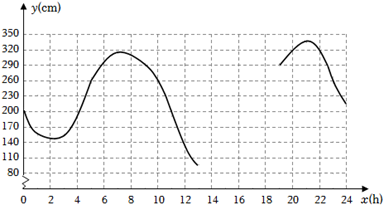
①根据表中数据,通过描点、连线(光滑曲线)的方式补全该函数的图象.
②观察函数图象,当x=4时,y的值为多少?当y的值最大时,x的值为多少?
请结合函数图象,写出该函数的两条性质或结论.
根据研究,当潮水高度超过260cm时,货轮能够安全进出该港口.请问当天什么时间段适合货轮进出此港口?
车速v(km/h) | 0 | 30 | 60 | 90 | 120 | 150 |
刹车距离s(m) | 0 | 7.8 | 19.2 | 34.2 | 52.8 | 75 |

①该型汽车车速越大,刹车距离越(填“大”或“小”);
②若该型汽车某次测试的刹车距离为40 m,估计该车的速度约为km/h;
第一步:列表;
|
x |
…… |
-7 |
-5 |
a |
-3 |
-2 |
0 |
1 |
2 |
3 |
5 |
…… |
|
|
…… |
-1 |
-1.5 |
-2 |
-3 |
-6 |
6 |
3 |
2 |
b |
1 |
…… |
第二步:描点;
第三步:连线.

①x的取值范围:;②y的取值范围:;
③图像的增减性:;④图像的对称性:;

|
x |
|
|
|
|
0 |
1 |
2 |
3 |
|
|
y |
|
|
m |
|
2 |
|
n |
|
|

①列表:请你补充表格中的数据:
|
|
0 |
0.5 |
1 |
1.5 |
2 |
2.5 |
3 |
|
|
0 |
3.125 |
|
3.375 |
|
0.625 |
0 |
②描点:请你把上表中各组对应值作为点的坐标,在平面直角坐标系中描出相应的点;
③连线:请你用光滑的曲线顺次连接各点.

①该糖果盒的最大容积是 ▲ ;
②若该糖果盒的容积超过
,请估计糖果盒的底边长
的取值范围.(保留一位小数)
实验观察:实验小组通过观察,每两小时记录一次电子秤读数,得到下表.
|
漏沙时间x(h) |
0 |
2 |
4 |
6 |
8 |
|
电子秤读数y(克) |
6 |
18 |
30 |
42 |
54 |

x | … | 1 | 2 | 3 | 4 | … | |||||||
y | … | m | 2 | n | … |

①当时,x=.
②写出该函数的一条性质.
③若方程有两个不相等的实数根,则t的取值范围是.
|
| … | | | | 0 | 2 | 3 | 4 | 5 | … |
| | … | | | | | 6 | | 2 | | … |
则表中 的值为.

|
x |
… |
|
|
|
|
0 |
1 |
2 |
3 |
4 |
… |
|
|
… |
|
a |
|
|
b |
|
|
|
|
… |
|
|
c |
d |
e |
f |
g |
①函数的图象关于y轴对称;
②当时,函数
有最小值,最小值为
;
③在自变量的取值范围内函数y的值随自变量x的增大而减小.
列表:下表是x与y的几组对应值,其中m=.
|
x |
… |
﹣3 |
﹣2 |
﹣1 |
|
|
1 |
2 |
3 |
… |
|
y |
… |
|
1 |
2 |
4 |
4 |
2 |
1 |
m |
… |
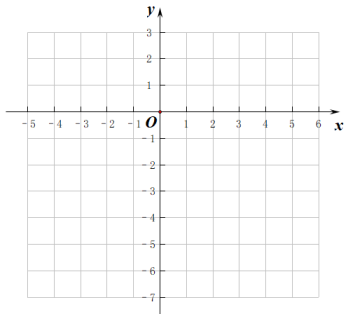
描点:根据表中各组对应值(x,y),在平面直角坐标系中描出各点,请你描出剩下的点;
连线:用平滑的曲线顺次连接各点,已经画出了部分图象,请你把图象补充完整;

①函数值y随x的增大而增大;②关于y轴对称;③
关于原点对称;
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
y | … | m | 0 | 1 | 2 | 1 | n | … |
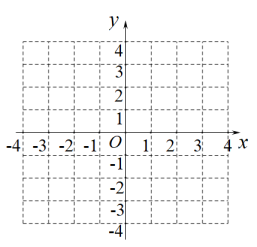
①方程有个解;
②若关于x的方程无解,则a的取值范围是.
x | … | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
y | … | m | 1 | n | 1 | 2 | 3 | 4 | … |
其中,,
.
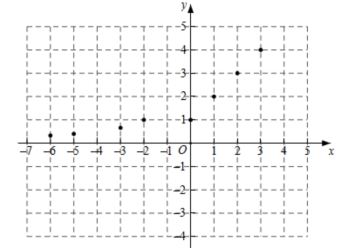
①点 ,
,
,
在函数图象上,则
▲
,
▲
;(填“>”,“=”或“<”);
②直线与图象相交,交点依次从左到右为M,N,K三点,如果
, 求t的值.
|
x |
… |
-2 |
-1 |
| 0 | | | | 3 | 4 | … |
| y | … | 1 | | 2 | 3 | 6 | 6 | m | | 1 | … |
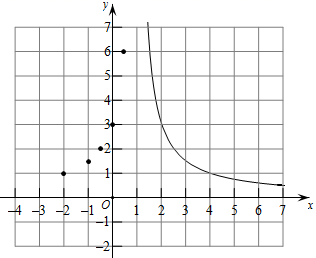
①通过观察、分析、证明,可知函数 的图象是轴对称图形,它的对称轴是;
②若点M( ,
)、N(
,
)在函数
的图象上,且1<
<
,则
(填 “ < ”或 “ > ”).

|
x |
⋯ |
﹣5 |
﹣4 |
﹣3 |
﹣2 |
﹣1 |
0 |
1 |
| 3 | 4 | 5 | 6 | 7 | ⋯ |
| y=| | ⋯ | | | | m | | 0 | 2 | 6 | 6 | n | | 3 | | ⋯ |

①列表:下表列出 点与R的几组对应值,请写出m,n的值:
,
;
| R | … | 3 | 4 | 5 | 6 | … |
| | … | 2 | 1.5 | 1.2 | 1 | … |
| | … | 3 | m | 2.2 | n | … |

②描点、连线:在平面直角坐标系中,以①给出的R的取值为横坐标,以 相对应的值为纵坐标,描出相应的点,并将各点用光滑曲线顺次连接起来;
① 随R的增大而;(填“增大”或“减小”)
②函数 的图象是由
的图象向平移个单位而得到.
解:设x2-2x-3=0,解得:x1=-1,x2=3,
则抛物线y=x2-2x-3与x轴的交点坐标为(-1,0)和(3,0).
画出二次函数y=x2-2x-3的大致图象(如图所示).
由图象可知:当-1<x<3时函数图象位于x轴下方,此时y<0,即x2-2x-3<0.
所以一元二次不等式x2-2x-3<0的解集为:-1<x<3.


通过对上述解题过程的学习,按其解题的思路和方法解答下列问题:
①转化思想;②分类讨论思想;③数形结合思想.
①自变量x的取值范围是▲;x与y的几组对应值如表,其中m=▲ .
|
x |
… |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
… |
|
y |
… |
5 |
0 |
-3 |
m |
-3 |
0 |
1 |
0 |
-3 |
… |
②如图,在直角坐标系中画出了函数y=-(x-1)(|x|-3)的部分图象,用描点法将这个图象补画完整.
③结合函数图象,解决下列问题:
解不等式:-3≤-(x-1)(|x|-3)≤0.

素材1:如图1,某路段(A-B-C-D 段)需要维修,临时变成双向交替通行,故在A,D处各设置红绿灯指导交通(仅设置红灯与绿灯).
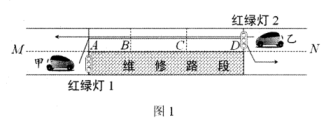
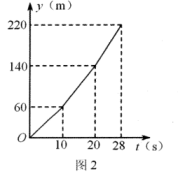
素材2:甲车先由A→D通行,乙车再由D→A通行,甲车经过AB,BC,CD段的时间分别为10s,10s,8s,它的路程y (m)与时间t(s)的关系如图2所示;两车经过BC段的速度相等,乙车经过AB段的速度是10m/s.
素材3:红绿灯1,2每114秒一个循环,每个循环内红灯、绿灯的时长如图3,且每次双向红灯时,已经进入AD段的车辆都能及时通过该路段.

[任务1]求A-B-C-D段的总路程和甲车经过BC段的速度.
[任务2]在图4中补全乙车通过维修路段时行驶的路程y(m)与时间t(s)之间的函数图象.
[任务3]丙车沿NM方向行驶,经DA段的车速与乙车经过时的速度相同,在DN段等红灯的车辆开始行驶后速度为8m/s,等红灯时车流长度每秒增加2m,问丙车在DN段从开始等待至离开点A至少需要几秒钟?


①写出该函数的一条性质;
②函数图象与x轴有个交点,所以对应的方程x2﹣2|x|+1=0有个实数根;
③方程x2﹣2|x|+1=1的解为;
④关于x的方程x2﹣2|x|+1=n有4个实数根时,n的取值范围是;
⑤将函数y=x2﹣2|x|+1的图象经过怎样的平移可以得到函数y=(x+2)2﹣2|x+2|﹣3的图象,直接写出平移过程.
列表:下表是与
的几组对应值,其中
;
1 | 2 | 3 | ||||||||
1 | 2 | 4 | 4 | 2 |
描点:根据表中各组对应值 , 在平面直角坐标系中描出了各点;
连线:用平滑的曲线顺次连接各点,画出了部分图象.请你把图象补充完整;
①;
②;
②探究思考:将①中“直线”改为“直线
”,其他条件不变,则S四边形OABC=;
③类比猜想:若直线交函数
的图象于A,B两点,连接
, 过点
作
交
轴于
, 则
.