备考2023年中考数学压轴题训练 ——相似（1）

更新时间：2023-05-14 浏览次数：97 类型：三轮冲刺

一、真题

1. (2022·嘉兴) 小东在做九上课本123页习题：“1： $\text{[math]}$ 也是一个很有趣的比．已知线段AB（如图1），用直尺和圆规作AB上的一点P，使AP：AB＝1： $\text{[math]}$ ．”小东的作法是：如图2，以AB为斜边作等腰直角三角形ABC，再以点A为圆心，AC长为半径作弧，交线段AB于点P，点P即为所求作的点．小东称点P为线段AB的“趣点”．
1. （1）你赞同他的作法吗？请说明理由．
2. （2）小东在此基础上进行了如下操作和探究：连结CP，点D为线段AC上的动点，点E在AB的上方，构造△DPE，使得△DPE∽△CPB．
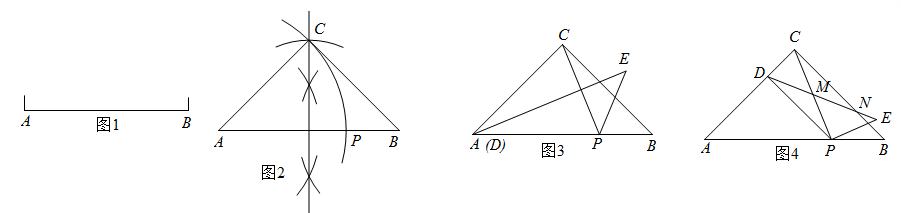
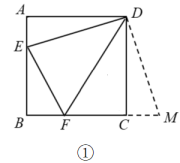
  ①如图3，当点D运动到点A时，求∠CPE的度数．
  
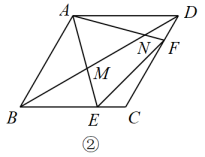
  ②如图4，DE分别交CP，CB于点M，N，当点D为线段AC的“趣点”时（CD＜AD），猜想：点N是否为线段ME的“趣点”？并说明理由．
答案解析收藏纠错 + 选题
2. (2022·湖州) 已知在Rt△ABC中，∠ACB=90°，a，b分别表示∠A，∠B的对边，a>b．记△ABC的面积为S．
1. （1）如图1，分别以AC，CB为边向形外作正方形ACDE和正方形BGFC．记正方形ACDE的面积为S₁ ，正方形BGFC的面积为S₂ ．
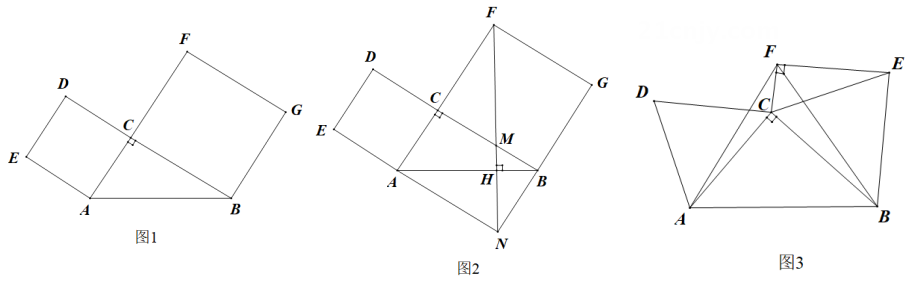
  ①若S₁=9，S₂=16，求S的值；
  
  ②延长EA交GB的延长线于点N，连结FN，交BC于点M，交AB于点H．若FH⊥AB（如图2所示），求证：S₂-S₁=2S．
2. （2）如图3，分别以AC，CB为边向形外作等边三角形ACD和等边三角形CBE，记等边三角形ACD的面积为S₁ ，等边三角形CBE的面积为S₂ ．以AB为边向上作等边三角形ABF（点C在△ABF内），连结EF，CF．若EF⊥CF，试探索S₂-S₁与S之间的等量关系，并说明理由．
答案解析收藏纠错 + 选题
3. (2023·仙桃模拟) 已知：点C，D均在直线l的上方， $\text{[math]}$ 与 $\text{[math]}$ 都是直线l的垂线段，且 $\text{[math]}$ 在 $\text{[math]}$ 的右侧， $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 相交于点O.
1. （1）如图1，若连接 $\text{[math]}$ ，则 $\text{[math]}$ 的形状为， $\text{[math]}$ 的值为；
2. （2）若将 $\text{[math]}$ 沿直线l平移，并以 $\text{[math]}$ 为一边在直线l的上方作等边 $\text{[math]}$ .
  ①如图2，当 $\text{[math]}$ 与 $\text{[math]}$ 重合时，连接 $\text{[math]}$ ，若 $\text{[math]}$ ，求 $\text{[math]}$ 的长；
  ②如图3，当 $\text{[math]}$ 时，连接 $\text{[math]}$ 并延长交直线l于点F，连接 $\text{[math]}$ .求证： $\text{[math]}$ .
答案解析收藏纠错 + 选题
4. (2022·苏州) 如图
1. （1）如图1，在△ABC中， $\text{[math]}$ ，CD平分 $\text{[math]}$ ，交AB于点D， $\text{[math]}$ // $\text{[math]}$ ，交BC于点E.
  ①若 $\text{[math]}$ ， $\text{[math]}$ ，求BC的长；
  
  ②试探究 $\text{[math]}$ 是否为定值.如果是，请求出这个定值；如果不是，请说明理由.
2. （2）如图2， $\text{[math]}$ 和 $\text{[math]}$ 是△ABC的2个外角， $\text{[math]}$ ，CD平分 $\text{[math]}$ ，交AB的延长线于点D， $\text{[math]}$ // $\text{[math]}$ ，交CB的延长线于点E.记△ACD的面积为 $\text{[math]}$ ，△CDE的面积为 $\text{[math]}$ ，△BDE的面积为 $\text{[math]}$ .若 $\text{[math]}$ ，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
5. (2022·扬州) 如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 边上由点 $\text{[math]}$ 向点 $\text{[math]}$ 运动（不与点 $\text{[math]}$ 重合），过点 $\text{[math]}$ 作 $\text{[math]}$ ，交射线 $\text{[math]}$ 于点 $\text{[math]}$ .
1. （1）分别探索以下两种特殊情形时线段 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系，并说明理由；
  ①点 $\text{[math]}$ 在线段 $\text{[math]}$ 的延长线上且 $\text{[math]}$ ；
  
  ②点 $\text{[math]}$ 在线段 $\text{[math]}$ 上且 $\text{[math]}$ .
2. （2）若 $\text{[math]}$ .
  ①当 $\text{[math]}$ 时，求 $\text{[math]}$ 的长；
  
  ②直接写出运动过程中线段 $\text{[math]}$ 长度的最小值.
答案解析收藏纠错 + 选题
6. (2023·博山模拟) 在数学兴趣小组活动中，同学们对菱形的折叠问题进行了探究.如图（1），在菱形 $\text{[math]}$ 中， $\text{[math]}$ 为锐角， $\text{[math]}$ 为 $\text{[math]}$ 中点，连接 $\text{[math]}$ ，将菱形 $\text{[math]}$ 沿 $\text{[math]}$ 折叠，得到四边形 $\text{[math]}$ ，点 $\text{[math]}$ 的对应点为点 $\text{[math]}$ ，点 $\text{[math]}$ 的对应点为点 $\text{[math]}$ .
1. （1）【观察发现】 $\text{[math]}$ 与 $\text{[math]}$ 的位置关系是；
2. （2）【思考表达】连接 $\text{[math]}$ ，判断 $\text{[math]}$ 与 $\text{[math]}$ 是否相等，并说明理由；
3. （3）如图（2），延长 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，请探究 $\text{[math]}$ 的度数，并说明理由；
4. （4）【综合运用】如图（3），当 $\text{[math]}$ 时，连接 $\text{[math]}$ ，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，请写出 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间的数量关系，并说明理由.
答案解析收藏纠错 + 选题

二、模拟预测

7. (2023九上·徐州期末) 我们知道：如图①，点B把线段AC分成两部分，如果 $\text{[math]}$ ＝ $\text{[math]}$ ，那么称点B为线段AC的黄金分割点.它们的比值为 $\text{[math]}$ .
1. （1）在图①中，若AC＝20cm，则AB的长为cm；
2. （2）如图②，用边长为20cm的正方形纸片进行如下操作：对折正方形ABCD得折痕EF，连接CE，将CB折叠到CE上，点B对应点H，得折痕CG.试说明：G是AB的黄金分割点；
3. （3）如图③，小明进一步探究：在边长为a的正方形ABCD的边AD上任取点E（AE＞DE），连接BE，作CF⊥BE，交AB于点F，延长EF、CB交于点P.他发现当PB与BC满足某种关系时，E、F恰好分别是AD、AB的黄金分割点.请猜想小明的发现，并说明理由.
答案解析收藏纠错 + 选题
8. (2022·山西模拟) 综合与时间
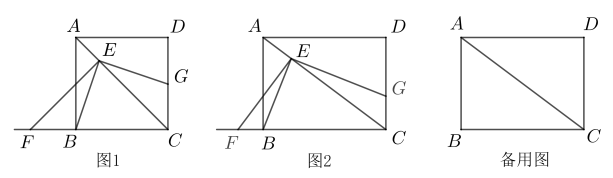
问题情境：如图1，在正方形ABCD中，点E是对角线AC上一点，连接BE，过点E分别作AC，BE的垂线，分别交直线BC，CD于点F，G.试猜想线段BF和CG的数量关系，并加以证明.
1. （1）数学思考：请解答上述问题.
2. （2）问题解决：如图2，在图1的条件下，将“正方形ABCD”改为“矩形ABCD”，其他条件不变.若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的值.
3. （3）问题拓展：在（2）的条件下，当点E为AC的中点时，请直接写出 $\text{[math]}$ 的面积.
答案解析收藏纠错 + 选题
9. (2023·苏州模拟) 【教材再现】
在初中数学教材中有这样一个基本事实：两条直线被一组平行线所截，所得的对应线段成比例.如图1，直线 $\text{[math]}$ ，直线m和直线n分别与直线 $\text{[math]}$ 和直线 $\text{[math]}$ 相交于点A，点B，点F，点D，直线m和直线n相交于点E，则 $\text{[math]}$ ；
【探究发现】
如图2，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点D在边 $\text{[math]}$ 上（不与点B，点C重合），连接 $\text{[math]}$ ，点E在边 $\text{[math]}$ 上， $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ ；
2. （2）当 $\text{[math]}$ 时，直接写出 $\text{[math]}$ 的长；
3. （3）点H在射线AC上，连接EH交线段 $\text{[math]}$ 于点G，当 $\text{[math]}$ ，且 $\text{[math]}$ 时，直接写出 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
10. (2023·苏州模拟)
1. （1）如图①，在正方形 $\text{[math]}$ 中，E，F分别是 $\text{[math]}$ ， $\text{[math]}$ 边上的动点，且 $\text{[math]}$ ，将 $\text{[math]}$ 绕点D逆时针旋转90°，得到 $\text{[math]}$ ，可以证明 $\text{[math]}$ ，进一步推出 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系为；
2. （2）在图①中，连接 $\text{[math]}$ 分别交 $\text{[math]}$ 和 $\text{[math]}$ 于P，Q两点，求证： $\text{[math]}$ ；
3. （3）如图②，在菱形 $\text{[math]}$ 中， $\text{[math]}$ ，点E，F分别是边 $\text{[math]}$ ， $\text{[math]}$ 上的动点（不与端点重合），且 $\text{[math]}$ ，连接 $\text{[math]}$ 分别与边 $\text{[math]}$ ， $\text{[math]}$ 交于M，N.当 $\text{[math]}$ 时，猜想 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间存在什么样的数量关系，并证明你的结论.
答案解析收藏纠错 + 选题
11. (2023·仙居模拟) 如图，正方形ABCD的边长为12 m，点E在AB上，AE＝8 m.正方形内存在匀强磁场，某种带电粒子以速度v（单位：m/s）沿着EF方向（EF⊥AB）从点E射入匀强磁场，在磁场中沿逆时针方向作匀速圆周运动，该圆与EF相切，半径r（单位：m）与v满足关系r＝kv（k为常数）. 如图1，当v＝8时，粒子恰好从点A处射出磁场.
1. （1） ①求常数k的值；
  ②若v＝8或6，粒子在磁场中的运动时间分别为t₁ ， t₂ ，请比较t₁ ， t₂的大小.
2. （2）如图2，若粒子从AD边上一点G射出磁场，请用无刻度的直尺和圆规画出粒子运动的弧形路径的圆心O（保留作图痕迹）.
3. （3）该种粒子能否从边CD上射出磁场？若能，请求出v的取值范围；若不能，请写出理由.
答案解析收藏纠错 + 选题
12. (2023·金华模拟) 如图1，在平面直角坐标系中，点O为坐标原点，点A的坐标为 $\text{[math]}$ ，直线 $\text{[math]}$ 经过点 $\text{[math]}$ 、 $\text{[math]}$ .将四边形 $\text{[math]}$ 绕点O按顺时针方向旋转α度得到四边形 $\text{[math]}$ ，此时直线 $\text{[math]}$ 、直线 $\text{[math]}$ 分别与直线 $\text{[math]}$ 相交于点P、Q.
1. （1）四边形 $\text{[math]}$ 的形状是，当 $\text{[math]}$ 时， $\text{[math]}$ 的值是；
2. （2） ①如图2，当四边形 $\text{[math]}$ 的顶点 $\text{[math]}$ 落在y轴正半轴上时，求 $\text{[math]}$ 的值；
  ②如图3，当四边形 $\text{[math]}$ 的顶点 $\text{[math]}$ 落在直线 $\text{[math]}$ 上时，求 $\text{[math]}$ 的面积；
3. （3）在四边形 $\text{[math]}$ 旋转过程中，当 $\text{[math]}$ 时，是否存在这样的点P和点Q，使得 $\text{[math]}$ ，若存在，请直接写出点P的坐标；若不存在，请说明理由.
答案解析收藏纠错 + 选题
13. (2023九下·永康月考) 如图，菱形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 是射线 $\text{[math]}$ 上的一个动点，将线段 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ 到 $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ ；
2. （2）如图2，连接 $\text{[math]}$ ， $\text{[math]}$ ，当 $\text{[math]}$ 与 $\text{[math]}$ 相似时，求 $\text{[math]}$ 的长；
3. （3）当点 $\text{[math]}$ 关于直线 $\text{[math]}$ 的对称点落在菱形的边上时，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
14. (2023九下·柯桥月考) 如图：
1. （1）【证明体验】如图(1)，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ 交 $\text{[math]}$ 于 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上， $\text{[math]}$ ，连接 $\text{[math]}$ ，求证： $\text{[math]}$ .
2. （2）【思考探究】如图(2)，在(1)的条件下，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长.
3. （3）【拓展延伸】如图(3)，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ，且 $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ $\text{[math]}$ ，则 $\text{[math]}$ .
答案解析收藏纠错 + 选题
15. (2023九下·义乌月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .已知动点 $\text{[math]}$ 从 $\text{[math]}$ 出发，以每秒 $\text{[math]}$ 个单位速度向 $\text{[math]}$ 运动，同时动点 $\text{[math]}$ 从 $\text{[math]}$ 出发，以都秒 $\text{[math]}$ 个单位的速度向 $\text{[math]}$ 运动，其中一个点到达终点时，另一个点随之停止运动.以 $\text{[math]}$ 为边在它的右侧作正方形 $\text{[math]}$ .设两点的运动时间为 $\text{[math]}$ .
1. （1）如图1，当 $\text{[math]}$ 时，求 $\text{[math]}$ 的边 $\text{[math]}$ 上的高 $\text{[math]}$ 的长；
2. （2）如图2，当点 $\text{[math]}$ 落在 $\text{[math]}$ 边上时，求 $\text{[math]}$ 的值.
3. （3）在动点 $\text{[math]}$ 运动的过程中，当正方形 $\text{[math]}$ 的某一边被 $\text{[math]}$ 的一边平分时，求出此时 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
16. (2023九下·宁波月考) 如图，矩形 $\text{[math]}$ 和矩形 $\text{[math]}$ 共顶点，且绕着点 $\text{[math]}$ 顺时针旋转，满足 $\text{[math]}$ .
1. （1）如图1，当D，E，B三点共线，且 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的比值；
2. （2）如图2， $\text{[math]}$ 的比值是否发生变化，若不变，说明理由；若变化，求出相应的值，并说明理由；
3. （3）如图3，若点F为 $\text{[math]}$ 的中点，且 $\text{[math]}$ ， $\text{[math]}$ ，连结 $\text{[math]}$ ，求 $\text{[math]}$ 的面积.
答案解析收藏纠错 + 选题
17. (2023九下·定海月考) 如图，已知P为锐角∠MAN内部一点，过点P作PB⊥AM于点B，PC⊥AN于点C，以PB为直径作⊙O，交直线CP于点D，连接AP，BD，AP交⊙O于点E.
1. （1）求证：∠BPD=∠BAC.
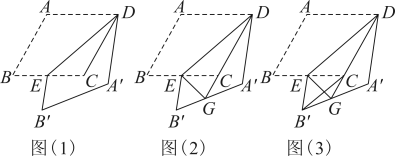
2. （2）连接EB，ED，当 tan∠MAN=2 AB= $\text{[math]}$ 时，在点P的整个运动过程中.
  ①若∠BDE=45°，求PD的长.
  
  ②若ΔBED为等腰三角形，求直接写出所有满足条件的BD的长.
3. （3）连接OC，EC，OC交AP于点F，当tan∠MAN=1，OC∥BE时，记ΔOFPP的面积为S₁ ， ΔCFE 的面积为S₂ ，请求出 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
18. (2023九下·杭州月考) 如图：

图1 图2
1. （1）如图1，在△ABC中，∠ACB＝2∠B，CD平分∠ACB，交AB于点D，DE∥AC，交BC于点E．
  ①若DE＝1，BD＝ $\text{[math]}$ ，求BC的长；
  
  ②试探究 $\text{[math]}$ 是否为定值．如果是，求出这个定值；如果不是，请说明理由．
2. （2）如图2，∠CBG和∠BCF是△ABC的2个外角，∠BCF＝2∠CBG，CD平分∠BCF，交AB的延长线于点D，DE∥AC，交CB的延长线于点E．记△ACD的面积为S₁ ， △CDE的面积为S₂ ， △BDE的面积为S₃ ．若S₁•S₃＝ $\text{[math]}$ S₂² ，求cos∠CBD的值．
答案解析收藏纠错 + 选题