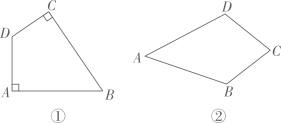

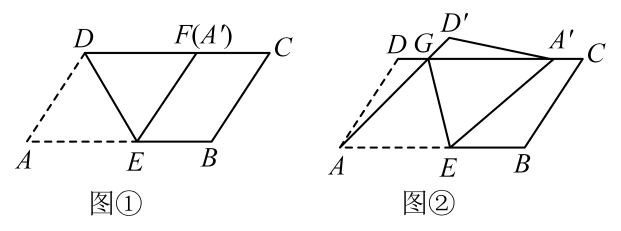
如图①,在四边形中,若
, 则四边形
是“准矩形”;
如图②,在四边形中,若
,
, 则四边形
是“准菱形”.
①一组对边平行的“准矩形”是矩形;
②一组对边相等的“准矩形”是矩形;
③一组对边相等的“准菱形”是菱形;
④一组对边平行的“准菱形”是菱形.
①若 , 求证:“准菱形”
是菱形;
②在①的条件下,连接 , 若
,
,
, 求四边形
的面积.

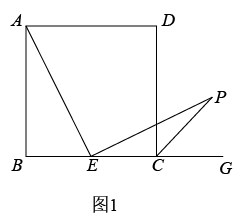
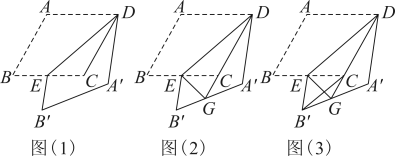
如图1,在正方形中,点
,
分别是
,
边上的动点,且
, 求证:
. 小明发现,当把
绕点
顺时针旋转90°至
, 使
与
重合时能够证明,请你给出证明过程.
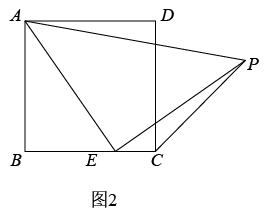
①如图2,在正方形中,如果点
,
分别是
,
延长线上的动点,且
, 则(1)中的结论还成立吗?若不成立,请写出
,
,
之间的数量关系(不要求证明)
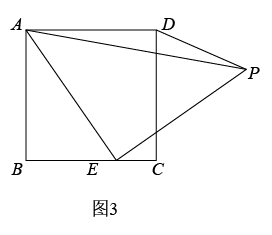
②如图3,如果点 ,
分别是
,
延长线上的动点,且
, 则
,
,
之间的数量关系是(不要求证明)
试判断四边形的形状,并说明理由;
如图①,若 , 请直接写出
的长.

A.矩形 B.菱形 C.正方形 D.平行四边形
其理论依据是.


求证:四边形为菱形.

当点正好落在
边上时,在图①中画出
的轴对称图形
, 并判断四边形
的形状是 ▲ ;
如图②,当点是线段
中点,且
时,求
的长;
如图③,当点、
、
在同一直线上,且
时,求
的长.



小明不完整的证明过程如下,请你帮他补充完整.
证明:如图,在BA上截取BH=BE,连接EH.
∵k=2, ∴AB=BC. ∵∠B=90°,BH=BE, ∴∠1=∠2=45°, ∴∠AHE=180°-∠1=135°. ∵CF平分∠DCG,∠DCG=90°, ∴∠3= ∴∠ECF=∠3+∠4=135°. ∴…… (只需在答题卡对应区域写出剩余证明过程) |
梅文鼎是我国清初著名的数学家,他在《勾股举隅》中给出多种证明勾股定理的方法图1是其中一种方法的示意图及部分辅助线.

在中,
, 四边形
、
和
分别是以
的三边为一边的正方形.延长
和
, 交于点
, 连接
并延长交
于点
, 交
于点
, 延长
交
于点
.
如图2,四边形和
分别是以
的两边为一边的平行四边形,探索在
下方是否存在平行四边形
, 使得该平行四边形的面积等于平行四边形
、
的面积之和.若存在,作出满足条件的平行四边形
(保留适当的作图痕迹);若不存在,请说明理由.