
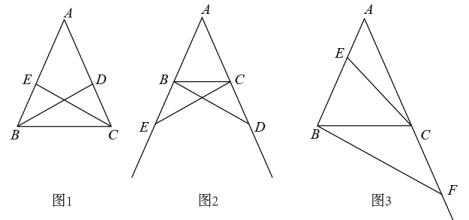
如图1,和
都是等边三角形,连接
. 求证:
.

如图2,和
都是等腰直角三角形,
. 连接
. 请直接写出
的值.
如图3,和
都是直角三角形,
, 且
. 连接
. 延长
交
于点F,交
于点G.求
的值.




如图1,点M是中
边的中点.

请你用圆规和无刻度的直尺过点M作的平行线
, 交
于点N;
如图2,线段与射线
有公共端点A,请你用圆规和无刻度的直尺在线段
上作一个点N,使
.

请解答上述问题;
如图2,在图1的条件下,将“正方形”改为“矩形
”,其他条件不变.若
,
, 求
的值;
在(2)的条件下,当点E为的中点时,请直接写出
的面积.
如图1,在和
中,
,
,
,
求证: . 我们在数学课上探索这一结论时进行了分析:要证
, 可设法证
, 若设
, 则只需证
.

请你根据以上分析,完成证明.
如图2,在四边形中,
,
,
, 求
的度数.

①探索、
和
的数量关系,并证明你的结论;
②如图3,若⊙O的半径为6, , 求边
的长;
③若 ,
, 直接写出
,
的数量关系.
问题情境:
数学活动课上,老师给出如下基础模型:如图①,已知 ,
, 过点C任作一条直线l(不与
重合),过点A作
于点D,过点B作
于点E,当点A、B在直线l同侧时,易证
(下列解题可直接用此结论).



小明不完整的证明过程如下,请你帮他补充完整.
证明:如图,在BA上截取BH=BE,连接EH.
∵k=2, ∴AB=BC. ∵∠B=90°,BH=BE, ∴∠1=∠2=45°, ∴∠AHE=180°-∠1=135°. ∵CF平分∠DCG,∠DCG=90°, ∴∠3= ∴∠ECF=∠3+∠4=135°. ∴…… (只需在答题卡对应区域写出剩余证明过程) |
①BD,CE是△ABC的角平分线.求证:BD=CE.
②点D,E分别是边AC,AB的中点,连接BD,CE.求证:BD=CE.
(从①②两题中选择一题加以证明)
经过做题反思,小明同学认为:在△ABC中,AB=AC,D为边AC上一动点(不与点A,C重合).对于点D在边AC上的任意位置,在另一边AB上总能找到一个与其对应的点E,使得BD=CE.进而提出问题:若点D,E分别运动到边AC,AB的延长线上,BD与CE还相等吗?请解决下面的问题:
如图2,在△ABC中,AB=AC,点D,E分别在边AC,AB的延长线上,请添加一个条件(不再添加新的字母),使得BD=CE,并证明.
如图3,在△ABC中,AB=AC=2,∠A=36°,E为边AB上任意一点(不与点A,B重合),F为边AC延长线上一点.判断BF与CE能否相等.若能,求CF的取值范围;若不能,说明理由.