阶梯 | 电量x(单位:度) | 电费价格(单位:元/度) |
一档 | 0<x≤180 | a |
二档 | 180<x≤400 | b |
三档 | x>400 | 0.95 |
刘同学说:“我乘出租车从市政府到娄底汽车站走了4.5千米,付车费11元.”
李同学说:“我乘出租车从市政府到娄底火车站走了6.5千米,付车费15元.”
问:
代收电费收据
电表号 | 1205 | 电表号 | 1205 |
户名 | 张磊 | 户名 | 张磊 |
月份 | 3月 | 月份 | 4月 |
用电量 | 220度 | 用电量 | 265度 |
金额 | 112元 | 金额 | 139元 |
小刘说:“我乘出租车从市政府到娄底汽车站走了4.5千米,付车费10.5元.”
小李说:“我乘出租车从市政府到娄底汽车站走了6.5千米,付车费14.5元.”
问:
| 计费项目 | 里程费 | 时长费 | 远途费 |
| 单价 | 1.8元每公里 | 0.45元每分钟 | 0.4元每公里 |
| 注:车费由里程费、时长费、远途费三部分组成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车10公里以内(含10公里)不收远途费,超过10公里的,超出部分每公里收0.4元。 | |||
小明和小亮在17:00-18:30之间各自乘坐滴滴快车回家,行车里程分别为9.5公里与14.5公里.如果下车时两人所付车费相同,问这两辆滴滴快车的行车时间相差( )分钟。
|
小明 |
小华 |
小芳 |
|
|
笔记本(本) |
15 |
24 |
27 |
|
钢笔(支) |
25 |
40 |
45 |
|
总价(元) |
330 |
528 |
585 |
租金(单位:元/台•时) | 挖掘土石方量(单位:m3/台•时) | |
甲型 | 190 | 160 |
乙型 | 260 | 240 |
A包装盒 | B包装盒 | |
每盒面包个数(个) | 3 | 8 |
每盒价格(元) | 5 | 11 |
若某同学正好买了50个面包,则他最少需要花( )元;
| 第一次 | 第二次 | |
| 甲种货车(量) | 2 | 5 |
| 乙种货车(量) | 3 | 6 |
| 累计运货(吨) | 13 | 28 |

| 甲型垃圾桶数量(套 | 乙型垃圾桶数量(套 | 总价(元 | |
| | 10 | 8 | 3680 |
| | 5 | 9 | 3140 |
| | | | 2680 |

时刻 | 12:00 | 13:00 | 14:00 |
里程碑上的数 | 是一个两位数,数字之和为7 | 十位数字和个位数字与12:00时看到的刚好相反 | 比12:00看到的两位数中间多了个0 |
则12:00时看到的两位数是( )

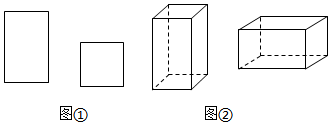
下表是工作人员四次领取纸板数的记录:
|
日期 |
正方形纸板(张) |
长方形纸板(张) |
|
第一次 |
356 |
544 |
|
第二次 |
422 |
860 |
|
第三次 |
500 |
1000 |
|
第四次 |
988 |
2022 |
仓库管理员在核查时,发现一次记录有误.则记录有误的是第次.

![]()