人教版七年级下数学期末复习知识点扫盲满分计划——9.3一元一...

更新时间：2023-05-22 浏览次数：66 类型：复习试卷

一、一元一次不等式组与二元一次方程

1. (2021七下·滁州期末) 已知关于x，y的方程组 $\text{[math]}$ 的解满足x≥0，y＜0．
1. （1）求m的取值范围；
2. （2）在m的取值范围内，当m取何整数时，不等式（2m+1）x＜2m+1的解集为x＞1？
答案解析收藏纠错 + 选题
2. (2021七下·仁寿期末) 关于x ， y的方程组 $\text{[math]}$ ，其中 $\text{[math]}$ .
1. （1）若x ， y的值互为相反数，求a的值；
2. （2）当 $\text{[math]}$ 时，求y的取值范围．
答案解析收藏纠错 + 选题
3. (2022七下·南宫期末) 若关于x，y的方程组 $\text{[math]}$ 的解x，y的值都小于1，则k的取值范围是（）

A . －3<k<1 B . －3≤k<1 C . －3<k≤1 D . －3≤k≤1

答案解析收藏纠错 + 选题
4. (2022七下·抚远期末) 已知关于x，y的方程组 $\text{[math]}$ 的解满足 $\text{[math]}$ ， $\text{[math]}$ ，则m的取值范围为．

答案解析收藏纠错 + 选题
5. (2022七下·崇川期末) 已知关于x，y的方程组 $\text{[math]}$ 的解都为非负数，a＋2b＝3，c＝3a－b，且b>0，则c的取值范围是．

答案解析收藏纠错 + 选题

二、列一元一次不等式组

6. (2023八上·金东期末) 为了美化校园，学校决定利用现有的2660盆甲种花卉和 $\text{[math]}$ 盆乙种花卉搭配A、B两种园艺造型共50个摆放在校园内，已知搭配一个A种造型需甲种花卉70盆，乙种花卉 $\text{[math]}$ 盆，搭配一个B种造型需甲种花卉40盆，乙种花卉 $\text{[math]}$ 盆.设搭配A种造型x个，你认为下列符合题意的不等式组是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022七下·前进期末) 把一筐苹果分给几个学生，如果每人分3个，那么余8个；如果每人分5个，那么最后一人分到，但不足3个．设学生有x人，列不等式组为．

答案解析收藏纠错 + 选题
8. (2021七下·东至期末) 随着网购的兴起，快递行业日渐繁荣，某物流公司计划调用甲、乙两种型号的物流 $\text{[math]}$ 辆，运送 $\text{[math]}$ 件 $\text{[math]}$ 种货物和 $\text{[math]}$ 件 $\text{[math]}$ 种货物，已知甲种物流货车每辆最多能载 $\text{[math]}$ 件 $\text{[math]}$ 种货物和 $\text{[math]}$ 件 $\text{[math]}$ 种货物，乙种物流货车每辆最多能载 $\text{[math]}$ 件 $\text{[math]}$ 种货物和 $\text{[math]}$ 件 $\text{[math]}$ 种货物．设安排甲种物流货车 $\text{[math]}$ 辆，你认为下列正确的不等式组是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022八下·茂名期中) 已知x＝2不是关于x的不等式2x-m＞4的整数解，x＝3是关于x的不等式2x-m＞4的一个整数解，则m的取值范围为（　　）

A . 0＜m＜2 B . 0≤m＜2 C . 0＜m≤2 D . 0≤m≤2

答案解析收藏纠错 + 选题
10. (2023七下·镇海期中) 《九章算术》中有这样的问题：今有5只雀、6只燕，分别聚集而用衡器称之，聚在一起的雀重，燕轻．将1只雀、1只燕交换位置而放，重量相等.5只雀、6只燕重量为1斤．问雀、燕每只各重多少？（注：该问题中的一斤为16两）设每只雀重x两，每只燕重y两，下列方程组中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

三、一元一次方程组的程序设计

11. (2022七下·乐亭期末) 运行程序如图所示，规定：从“输入一个值x”到“结果是否＞5”为一次程序操作，如果程序操作进行了两次才停止，那么x的取值范围是．

答案解析收藏纠错 + 选题
12. (2022七下·宁国期中) 如图，按下面的程序进行运算，规定程序运行到“判断结果是否大于35”为一次运算．若某运算进行了2次才停止，则 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
13. (2022八下·吉安月考) 如图，这是李强同学设计的一个计算机程序，规定从输入一个x值到判断结果是否≥15为一次运行过程，如果程序运行两次就停止，那么x的取值范是．

答案解析收藏纠错 + 选题
14. (2021七下·庐江期末) 已知某程序如图所示，规定：从“输入实数x”到“结果是否大于95”为一次操作，如果该程序进行了两次操作停止，那么实数x的取值范围是 $\text{[math]}$ $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
15. (2021七下·合肥期中) 按图中程序计算，规定：从“输入一个值x”到“结果是否≥14”为一次程序操作，如果程序操作进行了两次才停止，则x的取值范围为．

答案解析收藏纠错 + 选题

四、一元一次不等式组的分配问题

16. (2022七下·香坊期末) 把一些书分给几名同学，如果每人分3本，那么余8本；如果前面的每名同学分5本，那么最后一人就分不到3本，共有（）名同学．

A . 5 B . 6 C . 7 D . 8

答案解析收藏纠错 + 选题
17. 现在有住宿生若干名，分住若干间宿舍，若每间住4人，则还有19人无宿舍住；若每间住6人，则有一间宿舍不空也不满，若设宿舍间数为x，则可以列得不等式组为( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
18. (2019七下·巴中期中) 一筐橘子分给若干个儿童，如果每人分4个，则剩下9个；如果每人分6个，则最后一个儿童分得的橘子少于3个，问共几个儿童，分了多少个橘子？

答案解析收藏纠错 + 选题
19. (2022七下·五华期末) 将一箱苹果分给若干位小朋友，若每位小朋友分5个苹果，则还剩12个苹果，若每位小朋友分8个苹果，则有一位小朋友分到了苹果但不足8个，则有小朋友（）

A . 7位 B . 6位 C . 5或6位 D . 37或42位

答案解析收藏纠错 + 选题
20. (2022七下·岑溪期中) 有一家人参加登山活动，他们要将矿泉水分装在旅行包内带上山，若每人带2瓶，则剩余3瓶，若每人带3瓶，则有一人带了矿泉水，但不足2瓶，则这家参加登山的人数为（）

A . 4人 B . 5人 C . 3人 D . 5人或6人

答案解析收藏纠错 + 选题

五、一元一次不等式组的销售问题

21. (2022七下·前进期末) 某工厂有甲种原料66千克．乙种原料66.4千克，现计划用这两种原料生产A、B两种型号的产品共90件、已知每件A型号下需要甲种原料0.5千克，乙种原料0.8千克；每件B型号产品需要甲种原料1.2千克，乙种原料0.6千克．
1. （1）该工厂有哪几种生产方案？
2. （2）在这批产品全部售出的条件下，若1件A型号产品获利30元，1件B型号产品获利20元，（1）中哪种方案获利最大？最大利润是多少？
3. （3）在（2）的条件下，工厂决定将所获利润的25%全部用于再次购进甲、乙两种（两种原料都有）原料，且购进每种原料的数量均为正整数．若甲种原料每千克35元，乙种原料每千克55元．请直接写出购买甲、乙两种原料各多少千克
答案解析收藏纠错 + 选题
22. (2022七下·尧都期末) “平遥古城三件宝，漆器牛肉长山药．”平遥推光漆器因其历史悠久和独特的制作工艺，和福州脱胎漆器、扬州漆器、成都漆器并称为中国四大漆器．某漆器厂清明前生产 $\text{[math]}$ 、 $\text{[math]}$ 两种首饰盒，若生产 $\text{[math]}$ 件 $\text{[math]}$ 首饰盒和 $\text{[math]}$ 件 $\text{[math]}$ 首饰盒，共需投入成本 $\text{[math]}$ 元；若生产 $\text{[math]}$ 件 $\text{[math]}$ 首饰盒和 $\text{[math]}$ 件 $\text{[math]}$ 首饰盒，共需投入成本 $\text{[math]}$ 元．
1. （1）每件 $\text{[math]}$ ， $\text{[math]}$ 首饰盒的生产成本分别是多少元？
2. （2）该厂准备用不超过 $\text{[math]}$ 元的资金生产这两种首饰盒共 $\text{[math]}$ 件，且要求生产 $\text{[math]}$ 首饰盒数量不少于 $\text{[math]}$ 首饰盒数量的 $\text{[math]}$ 倍，问共有几种生产方案？
3. （3）将漆器供应给商场后，每件 $\text{[math]}$ 首饰盒可获利 $\text{[math]}$ 元，每件 $\text{[math]}$ 首饰盒可获利 $\text{[math]}$ 元，在（2）的前提下，请你设计出总获利最大的生产方案，并求出最大总获利．
答案解析收藏纠错 + 选题
23. (2022七下·湖里期末) 某商店决定购进A、B两种纪念品．若购进A种纪念品8件，B种纪念品3件，需要95元；若购进A种纪念品5件，B种纪念品6件，需要80元．
1. （1）求购进A、B两种纪念品每件各需多少元？
2. （2）若该商店决定购进这两种纪念品共100件，考虑市场需求和资金周转，用于购买这100件纪念品的资金不少于750元，但不超过764元，那么该商店共有几种进货方案？
3. （3）已知商家出售一件A种纪念品可获利a元，出售一件B种纪念品可获利（5﹣a）元，试问在（2）的条件下，商家采用哪种方案可获利最多？（商家出售的纪念品均不低于成本价）
答案解析收藏纠错 + 选题
24. (2022七下·浦北期末) 百货商店抓住旅游文化艺术节商机，决定购进甲、乙两种纪念品若购进甲种纪念品1件，乙种纪念品2件，需要160元：购进甲种纪念品2件，乙种纪念品3件，需要280元．
1. （1）购进甲、乙两种纪念品每件各需要多少元？
2. （2）该商店决定购进甲、乙两种纪念品共100件，并且考虑市场需求和资金周转，用于购买这些纪念品的资金不少于6300元，同时又不能超过6430元，则该商店共有几种进货方案？
3. （3）若销售每件甲种纪念品可获利30元，销售每件乙种纪念品可获利12元，在第（2）问中的各种进货方案中，哪种方案获利最大？最大利润是多少元？
答案解析收藏纠错 + 选题
25. (2022七下·樊城期末) 某商场若购进2部甲型号手机和3部乙型号手机，共需7400元；若购进3部甲型号手机和5部乙型号手机，共需11700元.
1. （1）求甲、乙型号手机每部的进价；
2. （2）商场计划用不少于44400元且不多于50000元的资金购进这两种型号手机共30部.
  ①求有多少种进货方案；
  
  ②若每部甲，乙型号手机的售价分别为2500元，1950元，采用①中甲型手机进货量最少的方案进货，为了促销.商场决定每售出一部甲型号手机，返还顾客现金a元，每售出一部乙型号手机，返还顾客现金b元（a≥50，b≥50且a、b为50的整数倍），要保证该进货方案（全都售完）获利达到16500元，直接写出a、b的值.
答案解析收藏纠错 + 选题

六、一元一次不等式的方案问题

26. (2023七下·怀宁期中) “绿水青山，就是金山银山”．某旅游景区为了保护环境，需购买 $\text{[math]}$ 、 $\text{[math]}$ 两种型号的垃圾处理设备，已知2台 $\text{[math]}$ 型设备和3台 $\text{[math]}$ 型设备日处理能力一共为72吨；3台 $\text{[math]}$ 型设备和1台 $\text{[math]}$ 型设备日处理能力一共为52吨．
1. （1）求1台 $\text{[math]}$ 型设备、1台 $\text{[math]}$ 型设备日处理能力各为多少吨？
2. （2）根据实际情况，需购买 $\text{[math]}$ 、 $\text{[math]}$ 两种型号的垃圾处理设备共10台．要求 $\text{[math]}$ 型设备不多于 $\text{[math]}$ 型设备的3倍，且购回的设备日处理能力不低于144吨．请你利用不等式的知识为该景区设计购买 $\text{[math]}$ 、 $\text{[math]}$ 设备的方案．
答案解析收藏纠错 + 选题
27. (2022七下·依安期末) 在城市创卫工作中为“保护好环境，拒绝冒黑烟”，某市公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车，计划购买A型和B型两种环保节能公交车共10辆，若购买A型公交车3辆，B型公交车2辆，共需600万元；若购买A型公交车2辆，B型公交车3辆，共需650万元．
1. （1）求购买A型和B型公交车每辆各需多少万元？
2. （2）预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次．若该公司购买A型和B型公交车的总费用不超过1200万元，且确保这10辆公交车在该线路的年均载客总和不少于680万人次，则该公司有哪几种购车方案？哪种购车方案总费用最少？最少总费用是多少？
答案解析收藏纠错 + 选题
28. (2022七下·长沙期末) “中国人的饭碗必须牢牢掌握在咱们自己手中”．为扩大粮食生产规模，某粮食生产基地计划投入一笔资金购进甲、乙两种农机具．已知购进3件甲种农机具和2件乙种农机具共需4万元，购进1件甲种农机具和4件乙种农机具共需3万元．
1. （1）求购进1件甲种农机具和1件乙种农机具各需多少万元？
2. （2）若该粮食生产基地计划购进甲、乙两农机具共10件，且投入资金不少于9万元又不超过10万元，则有哪几种购买方案？
3. （3）在（2）的条件下，哪种购买方案需要的资金最少，最少资金是多少？
答案解析收藏纠错 + 选题
29. (2022七下·高要期末) 湛江市正在创建“全国文明城市”，育才学校拟举办“创文知识”抢答赛，欲购买A、B两种奖品以鼓励抢答者．如果购买A种20件，B种15件，共需380元；如果购买A种15件，B种10件，共需280元．
1. （1） A、B两种奖品每件各多少元？
2. （2）现要购买A、B两种奖品共100件．
  ①若购买金额不超过900元，那么A种奖品最多购买多少件？
  ②若购买金额不低于860元，不超过900元，有哪几种购买方案？
答案解析收藏纠错 + 选题
30. (2022七下·广安期末) 某汽车租赁公司要购买轿车和面包车共10辆，已知轿车每辆7万元，面包车每辆4万元，其中轿车至少要购买3辆，且公司可投入的购车款不超过55万元．
1. （1）符合公司要求的购买方案有哪几种？
2. （2）如果每辆轿车的日租金为200元，每辆面包车的日租金为110元，假设新购买的这10辆车每日都可租出，要使这10辆车的日租金不低于1500元，那么该租赁公司应选择以上哪种购买方案？
答案解析收藏纠错 + 选题

七、综合训练

31. (2020七下·朝阳期末) 在近几年的两会中，有多位委员不断提出应在中小学开展编程教育，2019年3月教育部公布的《2019年教育信息化和网络安全工作要点》中也提出将推广编程教育．某学校的编程课上，一位同学设计了一个运算程序，如图所示．

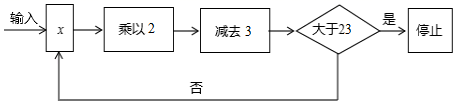
按上述程序进行运算，程序运行到“判断结果是否大于23”为一次运行．
1. （1）若x＝5，直接写出该程序需要运行多少次才停止；
2. （2）若该程序只运行了2次就停止了，求x的取值范围．
答案解析收藏纠错 + 选题
32. (2020七下·通州期中) 如图，这是王彬同学设计的一个计算机程序，规定从“输入一个值x”到判断“结果是否≥13”为一次运行过程．如果程序运行两次就停止，那么x的取值范围是（　　）

A . x≥4 B . 4≤x＜7 C . 4＜x≤7 D . x≤7

答案解析收藏纠错 + 选题
33. (2022七下·连山期末) 有一个正的两位数，它的个位数字是十位数字的2倍小1，并且这个两位数不大于35，设十位数字为x，那么满足x的不等式组是．

答案解析收藏纠错 + 选题
34. (2021七下·萧山期中) 陈老师购了一批笔记本，用于奖励期中考试成绩优异和进步快的同学，同学们想知道笔记本的本数，陈老师让他们猜.陈茜说：“至少13本.”江涵说：“至多11本.”江月说：“至多8本.”陈老师说：“你们三个人都说错了”.则这批笔记本有本.

答案解析收藏纠错 + 选题
35. (2022七下·岑溪期中) 如图所示，运行程序规定：从“输入一个值x”到“结果是否大于79”为一次程序操作，如果程序操作进行了三次才停止，那么x的取值范围是.

答案解析收藏纠错 + 选题
36. (2022七下·仁寿期中) 某汽车专卖店销售A，B两种型号的新能源汽车．第一周售出1辆A型车和3辆B型车，销售额为96万元；第二周售出2辆A型车和1辆B型车，销售额为62万元．
1. （1）求每辆A型车和B型车的售价各为多少万元；
2. （2）甲公司拟向该店购买A、B两种型号的新能源汽车共6辆，且A型号车不少于2辆，购车费不少于130万元，则有哪几种购车方案？
3. （3）为了提高营业额，除了A、B两种型号，第三周、第四周专卖店新增了售价为12万元的C种型号的汽车．据统计，第三周第四周总营业额达到380万元，且A、B两种型号共卖出10辆，C不少于12辆，则A型车至少卖出了几辆？
答案解析收藏纠错 + 选题

37. (2021七下·吴中期末) 为庆祝建党100周年，学校党支部号召广大党员积极开展“学知识、获积分、赢奖品!”活动，该校准备到苏宁电器超市采购奖品，发现该超市销售 $\text{[math]}$ 、 $\text{[math]}$ 两种型号的电风扇， $\text{[math]}$ 型号每台进价为190元、 $\text{[math]}$ 型号每台进价为160元，下表是近两周的销售情况：

销售时段	销售数量		销售额
销售时段	$\text{[math]}$ 种型号	$\text{[math]}$ 种型号	销售额
第一周	3台	3台	1320元
第二周	2台	6台	1680元

（进价、售价均保持不变，利润=销售收入-进货成本）

（1）求 $\text{[math]}$ 、 $\text{[math]}$ 两种型号的电风扇的销售单价：
（2）若超市准备再采购40台这两种型号的电风扇，且 $\text{[math]}$ 型号电风扇采购数量不超过 $\text{[math]}$ 型号数量的2倍，当这40台电风扇全部出售给学校且利润不低于1850元，求超市共有哪些采购方案?

答案解析收藏纠错 + 选题

38. (2021七下·铜梁期末) 今年6月初，由于持续暴雨，某市遭受严重水涝灾害，群众失去家园，市民政局为解决灾民困难，紧急组织了一批救灾帐篷和食品准备送往灾区.已知这批物质中，帐篷和食品共320件，且帐篷比食品多80件.

（1）求帐篷和食品各有多少件？

（2）现计划租用 $\text{[math]}$ 两种货车共8辆，一次性将这批物质全部送到灾民手中，已知两种货车可装帐篷和食品的件数以及每辆货车所需付运费情况如下表，求出运费最少的方案？最少运费是多少？

	帐篷（件）	食品（件）	每辆需付运费（元）
$\text{[math]}$ 种货车	40	10	780
$\text{[math]}$ 种货车	20	20	700

答案解析收藏纠错 + 选题

39. (2022七下·抚远期末) 已知不等式组 $\text{[math]}$ 解集为 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . 1 B . 2022 C . -1 D . -2022

答案解析收藏纠错 + 选题
40. (2022七下·容县期末) 已知关于 $\text{[math]}$ ， $\text{[math]}$ 的方程组 $\text{[math]}$ 的解为整数，且关于 $\text{[math]}$ 的不等式组 $\text{[math]}$ 有且仅有3个整数解，则所有满足条件的整数a的和为.

答案解析收藏纠错 + 选题
41. (2022七下·泗洪期末) 南京火车货运站现有甲种货物1530吨，乙种货物1150吨，某公司将安排一列火车将这批货物运往上海，这列火车可挂 $\text{[math]}$ 、 $\text{[math]}$ 两种不同型号货厢50节
1. （1）已知甲种货物35吨和乙种货物15吨可装满一节 $\text{[math]}$ 型货厢，甲种货物25吨和乙种货物35吨可装满一节 $\text{[math]}$ 型货厢，运输这批货物有几种安排货厢方案？
2. （2）若一节 $\text{[math]}$ 型货厢的运费是0.5万元，一节 $\text{[math]}$ 型货厢的运费是0.8万元，如何安排运输方案，才能使得运费最少？并求出最少运费．
答案解析收藏纠错 + 选题
42. (2022七下·资阳期末) 若关于 $\text{[math]}$ 的一元一次不等式组 $\text{[math]}$ 的解集是 $\text{[math]}$ ，且 $\text{[math]}$ 为非正整数，则满足条件的 $\text{[math]}$ 的取值有（）个.

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
43. (2022七下·泗洪期末) 已知：关于 $\text{[math]}$ 、 $\text{[math]}$ 的方程组： $\text{[math]}$
1. （1）求这个方程组的解：（用含有字母 $\text{[math]}$ 的代数式表示）
2. （2）若这个方程组的解满足 $\text{[math]}$ 为非负数， $\text{[math]}$ 为负数，求字母 $\text{[math]}$ 的取值范围
答案解析收藏纠错 + 选题
44. (2023八下·南山期中) 某校为了更好地开展球类运动，体育组决定用1600元购进足球8个和篮球14个，已知篮球的单价比足球的单价多20元，请解答下列问题：
1. （1）求出足球和篮球的单价；
2. （2）若学校欲用不超过3240元，且不少于3200元再次购进两种球50个，求出有哪几种购买方案？
答案解析收藏纠错 + 选题