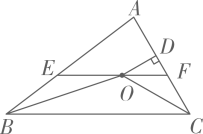



①到两工厂的距离相等;
②在内,且到两条公路的距离相等.
你能帮忙确定仓库的位置吗?(保留作图痕迹,不写作法)

⑴△ABC的面积为 ▲;
⑵在DE的右侧找一点F,使得△DEF与△ABC全等;
⑶画△ABC中BC边上的高AH.
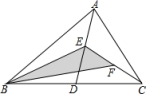
连接 , 由
得
,
同理,可得 .
设 ,
, 则
,
.
由题意得 ,
.
可列方程组 , 解得,
通过解这个方程组可得四边形的面积为;

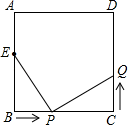
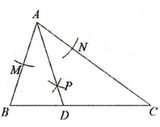
∴∠PBC=∠ABC,∠PCD=
▲ ,
∵∠PCD= ▲ +∠P,
∴∠P=∠PCD﹣ ▲ ,
=(∠ACD﹣∠ABC
= ▲ .

如图②,若α=225°,求∠P的度数.


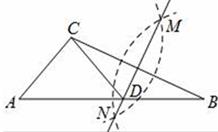
①试猜测PB和PC的数量关系,并说明理由;
②若△ADP的面积为5,求四边形ABCD的面积.
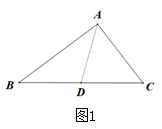
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE,容易证得△ADC≌△EDB,再由“三角形的三边关系”可求得AD的取值范围是.
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.