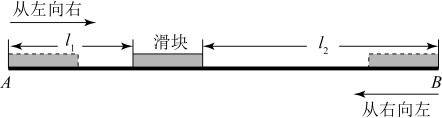
①关于的方程
的解为
;
②一次函数(
)图像上任意不同两点
和
满足:
;
③若(
),则
;
④若 , 且
, 则当
时,
.





型号 | 甲 | 乙 | 丙 |
进价(万元/台) | 0.9 | 1.2 | 1.1 |
售价(万元/台) | 1.2 | 1.6 | 1.3 |

|
为家人选择更优惠的快递公司活动报告 ⑴收集信息 经了解我家附近有甲、乙两个不同的快递公司代办点,服务质量同等,爸爸妈妈邮寄快递通常是随机去其中的一个代办点,他们邮寄的快递都是省外且在10kg以内,体积一般较小. 快递费通常是由首重费和续重费组成,以1kg为单位计费,不足1kg按1kg计费.取实际重量和体积重量(长×宽×高/6000,单位cm)中两者较大值作为物品重量计费. 甲、乙两个代办点省外邮寄费用标准如下: 甲:首重1kg收费8元,续重5元/kg;(即所寄物品重量不超过1kg时收费8元,重量超过1kg时超过部分按每千克加收5元计费) 乙:首重1kg收费10元,续重4元/kg. ⑵建立模型 ①发现所寄物品的快递费用y(元)与物品重量x(kg)之间存在函数关系,y与x之间的关系式为: ②在同一平面直角坐标系内画出两个函数的图象(如图,不完整),两图象交于点A.
⑶解决问题 我们可以根据图象推断哪个快递公司更优惠,结论如下: |
任务:

①请问一次函数的图象是否经过某个定点,若经过,请求出定点坐标;若不经过,请说明理由;
②一次函数(
, k、b为常数)的衍生函数图象与
恰好有两个交点,求b的取值范围.