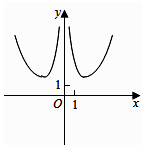
 B .
B . 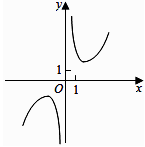 C .
C .  D .
D . 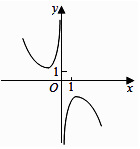
某地区2022年8月份每天最高气温与最低气温
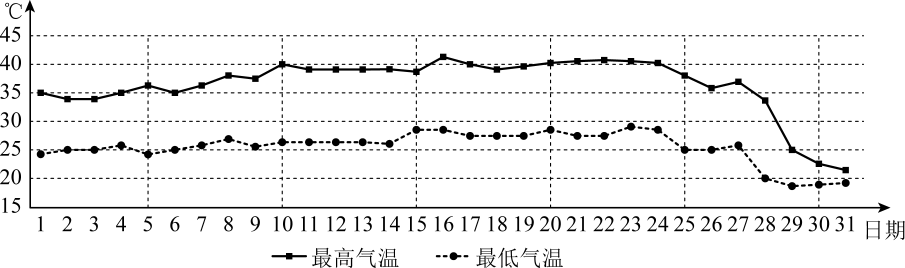
根据图表判断,以下结论正确的是()
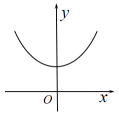 B .
B . 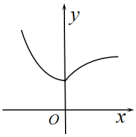 C .
C . 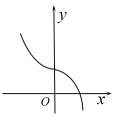 D .
D . 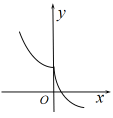
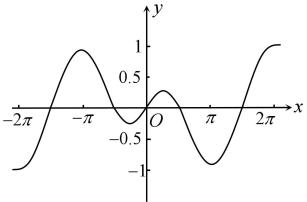 B .
B .  C .
C . 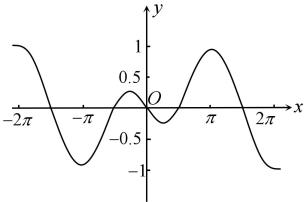 D .
D . 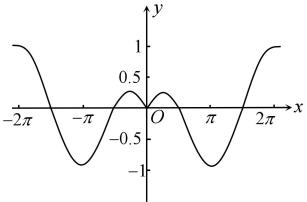
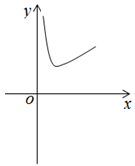 B .
B . 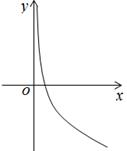 C .
C . 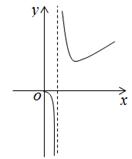 D .
D . 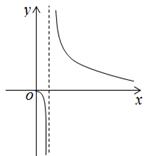
①当 时,
;②
为偶函数

① ;② 对任意
,都有
;
③ 对任意 ,且
,都有
;
其中所有正确结论的序号是;
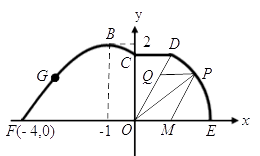
(Ⅰ)设l与C1相交于A,B两点,求|AB|;
(Ⅱ)若把曲线C1上各点的横坐标压缩为原来的 倍,纵坐标压缩为原来的
倍,得到曲线C2 , 设点P是曲线C2上的一个动点,求它到直线l的距离的最小值.
已知直线l: 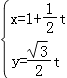 (t为参数),曲线C1:
(t为参数),曲线C1: ![]() (θ为参数).
(θ为参数).
(Ⅰ)设l与C1相交于A,B两点,求|AB|;
(Ⅱ)若把曲线C1上各点的横坐标压缩为原来的 倍,纵坐标压缩为原来的
倍,得到曲线C2 , 设点P是曲线C2上的一个动点,求它到直线l的距离的最小值.