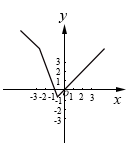
 B .
B . 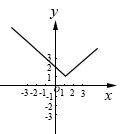 C .
C . 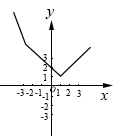 D .
D . 
①关于的方程
的解为
;
②一次函数(
)图像上任意不同两点
和
满足:
;
③若(
),则
;
④若 , 且
, 则当
时,
.
①当时,函数
的图象与
轴的交点是
;
②当时,函数
以的图象与
轴的交点是
;
③不论为任意常数,函数
的最小值都是0;
④若图象在直线
下方的点的横坐标
满足
, 则
的取值范围为
.
①当x=2时,y2﹣y1=2,求a的取值范围.
②若点P的坐标是(1,1),且a>b,求证:当x=2时,y1﹣y2<
①直接写出该函数与y轴的交点坐标;
②若直线y=4x+t与该函数只有一个交点,求t的取值范围;
① ,
,
.
②P为关于1的对称函数图象上一点(点P不与点C重合),当 时,求点P的坐标;

| x | …… | -3 | -2 | -1 | 0 | 1 | 2 | 3 | …… |
| y | …… | 6 | 4 | 2 | 0 | 2 | 4 | 6 | …… |
经历同样的过程画函数 和
的图象如下图所示,观察发现:三个函数的图象都是由两条射线组成的轴对称图形:三个函数解析式中绝对值前面的系数相同,则图象的开口方向和形状完全相同,只有最高点和对称轴发生了变化.




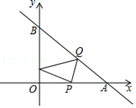
如图3,点A坐标为 , 点B坐标为
, 点B与点
关于直线
对称,连接
与直线
交于点C , 则点C的坐标为.
如图1所示的网格中,建立平面直角坐标系.先画出正比例函数的图象,再画出
关于正比例函数
的图象对称的
.
猜想:点关于正比例函数
的图象对称的点Q的坐标为;
验证点在第一象限时的情况(请将下面的证明过程补充完整).
证明:如图2,点、Q关于正比例函数
的图象对称,
轴,垂足为H .