 B .
B .  C .
C .  D .
D . 
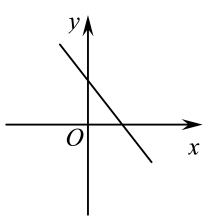 B .
B .  C .
C . 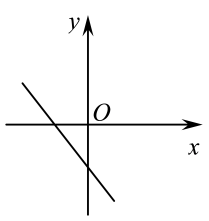 D .
D . 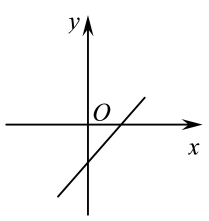



| 直播间 | 活动 |
| 甲 | 全场六折 |
| 乙 | “满 100 送 100 ” (如: 购买 190 元商品,赠 100 元购物券;购买 200 元商品, 赠200 元购物券) |
| 丙 | “满 100 堿 50” (如 : 购买 190 元商品,只需付 140 元; 购买 200 元商品,只需付100 元) |
请根据上述信息,解答下列问题:

【问题情境】“漏壶”是一种古代计时器,在社会实践活动中,某小组同学根据“漏壶”的原理制作了如图(a)所示的液体漏壶,该漏壶是由一个圆锥和一个圆柱组成的,中间连通,液体可以从圆锥容器中匀速漏到圆柱容器中,实验开始时圆柱容器中已有一部分液体.

【实验观察】下表是实验记录的圆柱容器液面高度与时间
的数据:
| 时间 | 1 | 2 | 3 | 4 | 5 |
| 6圆柱容器液面高度 | 6 | 10 | 14 | 18 | 22 |
请你根据表中的数据在图(b)中描点、连线,用所学过的一次函数的知识确定与
之间的函数表达式;
如果本次实验记录的开始时间是上午 , 那么当圆柱容器液面高度达到
时是几点?
确定文具套餐售价 | |
素材1 | 某书店销售一款文具套装,当每套文具售价为30元时,月销售量为200套,经市场调查表明,每套文具售价每降价1元,则月销售量增加20套.设每套文具的售价为x元(x为正整数),月销售量为y套. |
素材2 | 该文具套装的成本是10元/套. |
素材3 | 为促进公益,在售价不低于进价且每套文具获利不高于95%的前提下,该书店决定,每月捐赠400元给慈善机构. |
问题解决:
求y关于x的函数表达式.
当售价为多少时,月利润W获得最大?最大利润是多少?
为了保证捐款后月利润不低于3040元,文具套装的售价可以取哪些数值.