备考2024年浙江中考数学一轮复习专题19.1三角形（1） ...

更新时间：2024-03-02 浏览次数：45 类型：一轮复习

一、选择题（每题3分，共30分）

1. (2023八上·东阳月考) $\text{[math]}$ 三个内角的度数之比为3：4：5，那么 $\text{[math]}$ 是（）

A . 等腰三角形 B . 锐角三角形 C . 钝角三角形 D . 直角三角形

答案解析收藏纠错 + 选题
2. (2022八上·新昌期中) 如图，M，A，N是直线l上的三点，AM=3 ， AN=5， P是直线l外一点，且∠PAN＝60°， AP=1，若动点Q从点M出发，向点N移动，移动到点N停止，在△APQ形状的变化过程中，依次出现的特殊三角形是（）

A . 直角三角形—等边三角形—直角三角形—等腰三角形 B . 直角三角形—等腰三角形—直角三角形—等边三角形 C . 等腰三角形—直角三角形—等腰三角形—直角三角形 D . 等腰三角形—直角三角形—等边三角形—直角三角形

答案解析收藏纠错 + 选题
3. (2023八上·吴兴期中) 如图，AB＝AD，∠BAD＝140°，AB⊥CB于点B，AD⊥CD于点D，E、F分别是CB、CD上的点，且∠EAF＝70°，下列结论中①DF＝BE，②△ADF≌△ABE，③FA平分∠DFE，④EF平分∠AEC，⑤BE+DF＝EF．其中正确的结论是（）

A . ④⑤ B . ①② C . ③⑤ D . ①②③

答案解析收藏纠错 + 选题
4. (2023八上·萧山月考) 如图，在△ABC中，AD是角平分线，AE是高，已知∠BAC＝2∠B ， ∠B＝4∠DAE ，那么∠C的度数为（）

A . 75° B . 72° C . 70° D . 60°

答案解析收藏纠错 + 选题
5. (2023八上·杭州月考) 将长方形纸片ABCD如图折叠，B ， C两点恰好重合在AD边上的同一点P处，折痕分别是MH ， NG ，若∠MPN=90°，PM=3，MN=5，分别记△PHM ， △PNG ， △PMN的面积为S₁ ， S₂ ， S₃ ，则S₁ ， S₂ ， S₃之间的数量关系是（）

A . S₃=S₁+S₂ B . 3S₃=2S₁+2S₂ C . S₃=5S₂-5S₁ D . 2S₃=3S₂-S₁

答案解析收藏纠错 + 选题
6. (2023八上·肇庆月考) 一个三角形的三个内角中，至少有（）

A . 一个锐角 B . 两个锐角 C . 一个钝角 D . 一个直角

答案解析收藏纠错 + 选题
7. (2024九上·乌鲁木齐期末) 一个图形经过下列变换后得到新图形，不能全等的是（　　）

A . 平移 B . 翻折 C . 旋转 D . 缩小

答案解析收藏纠错 + 选题
8. (2023八上·潮南期末) 如图，点F，C在BE上，△ABC≌△DEF，AB和DE，AC和DF是对应边，AC，DF交于点M，则∠AMF等于（）

A . 2∠B B . 2∠ACB C . ∠A＋∠D D . ∠B＋∠ACB

答案解析收藏纠错 + 选题
9. (2024八下·冷水滩开学考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ 交 $\text{[math]}$ 于点D ， $\text{[math]}$ 平分 $\text{[math]}$ 交 $\text{[math]}$ 于点E ， $\text{[math]}$ ， $\text{[math]}$ 交于点F ．则下列说法正确的有（）
① $\text{[math]}$ ；② $\text{[math]}$ ；③若 $\text{[math]}$ ，则 $\text{[math]}$ ；④ $\text{[math]}$ ．

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
10. (2024八上·长春净月高新技术产业开发期末) 如图，要测量池塘两岸相对的两点 $\text{[math]}$ ， $\text{[math]}$ 间的距离，小明在池塘外取 $\text{[math]}$ 的垂线 $\text{[math]}$ 上的点 $\text{[math]}$ ， $\text{[math]}$ ，使 $\text{[math]}$ ．再画出 $\text{[math]}$ 的垂线 $\text{[math]}$ ，使 $\text{[math]}$ 与 $\text{[math]}$ ， $\text{[math]}$ 在一条直线上，这时测得 $\text{[math]}$ 的长就是 $\text{[math]}$ 的长．依据是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（每题3分，共18分）

11. (2024八上·杭州期末) 已知三角形三条边分别为a＋4，a＋5，a＋6，则a的取值范围是．

答案解析收藏纠错 + 选题
12. (2023九上·萧山期中) 如图，AD、CE是△ABC的中线，若△CDG的面积是1，则△ABC的面积为．

答案解析收藏纠错 + 选题
13. (2023八上·印江期中) 造房子时屋顶常用三角结构，从数学角度来看，是应用了；而活动挂架则用了四边形的．

答案解析收藏纠错 + 选题
14. (2024七下·宁海期中) 一副三角板按如图所示放置，将含30°角的三角板固定，含45°角的三角板绕A点旋转，保持∠1为锐角，旋转过程中有下列结论：①∠1＝∠3；②若∠2＝45°，则AC∥DE．③若∠4＝∠B，则AC∥DE；④若∠1＝15°，则BC∥DE．其中正确的有．（填序号）

答案解析收藏纠错 + 选题
15. (2024九上·乌鲁木齐期末) 如图，在边长为6的等边△ABC中，点E，F分别是边AC，BC上的动点，且AE＝CF，连接BE，AF交于点P，连接CP，则CP的最小值为．

答案解析收藏纠错 + 选题
16. (2024八上·炎陵期末) 如图， $\text{[math]}$ ， $\text{[math]}$ ，添加一个条件，使得 $\text{[math]}$ ．

答案解析收藏纠错 + 选题

三、作图题（共6分）

17. (2023八上·萧山期中) 如图，在△ABC中，∠C＝90°．
1. （1）点D在边AC上，且点D到∠B两边的距离相等，用直尺和圆规作出点D（不写作法，保留作图痕迹，在图上清楚地标注点D）；
2. （2）在第（1）题的条件下，如果BC＝12，AC=5 ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题

四、解答题（共6题，共48分）

18. (2024八上·东莞期末)
如图，△ABC中，AB=AC，∠C=70°，作AB的垂直平分线交AB于E，交AC于D，求∠DBC的度数．

答案解析收藏纠错 + 选题
19. (2024八下·南城期中) 如图，△ABC是等边三角形，BD⊥AC，AE⊥BC，垂足分别为D、E，AE、BD相交于点O，连接DE．
1. （1）判断△CDE的形状，并说明理由．
2. （2）若AO＝12，求OE的长．
答案解析收藏纠错 + 选题
20. (2024八上·浙江期末) 如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，AC=8，BC=6，E，F分别是直线AC，AB上的动点，连结EF.
1. （1）求CD的长.
2. （2）若点E在边AC上，且3AE=2CE，EF⊥AC，求证：CF平分∠ACD.
3. （3）是否存在点E，F，使得以C，E，F为顶点的三角形与△CDF全等?若不存在，请说明理由；若存在，求出所有符合条件的DF的长.
答案解析收藏纠错 + 选题
21. (2023八上·期中) 在Rt△ABC中，∠ACB＝90°，M是边AB的中点，CH⊥AB于点H，CD平分∠ACB．
1. （1）求证：CD平分∠MCH；
2. （2）过点M作AB的垂线交CD的延长线于点E，
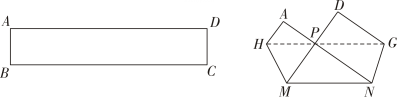
  ①求证：CM＝EM；
  ②△AEM是什么三角形？证明你的猜想．
答案解析收藏纠错 + 选题
22. (2023八上·舟山月考) 小明利用一根3m长的竿子来测量路灯的高度．他的方法是这样的：在路灯前选一点 $\text{[math]}$ ，使 $\text{[math]}$ m，并测得 $\text{[math]}$ ，然后把竖直的竿子 $\text{[math]}$ （ $\text{[math]}$ m）在 $\text{[math]}$ 的延长线上移动，使 $\text{[math]}$ ，此时量得 $\text{[math]}$ m．根据这些数据，小明计算出了路灯的高度．你知道小明计算的路灯的高度是多少？为什么？

答案解析收藏纠错 + 选题
23. (2023七下·嵊州期末) 将一副直角三角板 $\text{[math]}$ 和 $\text{[math]}$ 如图（1）放置，此时 $\text{[math]}$ 四点在同一条直线上，点A在边 $\text{[math]}$ 上，其中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ 的度数；
2. （2）将图（1）中的三角板 $\text{[math]}$ 绕点A以每秒 $\text{[math]}$ 的速度，按顺时针方向旋转一定的角度 $\text{[math]}$ 后，记为三角板 $\text{[math]}$ ，设旋转的时间为t秒．
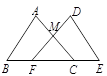
  ①当旋转至图（2）时，此时 $\text{[math]}$ ，求a的值；
  ②若在旋转过程中，三角板 $\text{[math]}$ 的某一边恰好与 $\text{[math]}$ 所在的直线平行，直接写出t的值．
答案解析收藏纠错 + 选题

五、实践探究题（共2题，共18分）

24. (2023八上·柯桥期中)
1. （1）【问题发现】
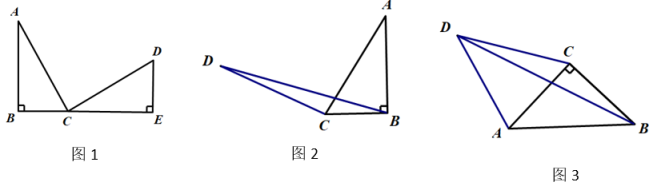
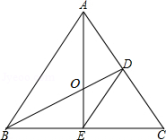
  如图1，在△ABC与△CDE中，∠B=∠E=∠ACD＝90°，AC＝CD，B、C、E三点在同一直线上，AB＝4，ED＝3，则BE=.
2. （2）【问题提出】
  如图2，在Rt△ABC中，∠ABC＝90°，BC＝3，过点C作CD⊥AC，且CD＝AC，求△BCD的面积.
3. （3）【问题解决】
  如图3，四边形ABCD中，∠ABC=∠CAB=∠ADC＝45°，△ACD面积为14且CD的长为7，求△BCD的面积.
答案解析收藏纠错 + 选题
25. (2023八上·萧山期中) 如图
1. （1）如图1，把一块三角板（AB＝BC，∠ABC＝90°）放入一个“U”形槽中，使三角形的三个顶点A，B，C分别在槽的两壁及底边上滑动，已知∠D＝∠E＝90°，在滑动过程中；你发现线段AD与BE有什么数量关系？试说明你的结论
2. （2）【变式探究】如图2，在△ABC中，点D、E、F分别在边BC、AB、AC上，若∠B＝∠FDE＝∠C，那么∠BED与∠CDF有何关系，并加以说理；
3. （3）【拓展应用】如图3，在△ABC中，BA=BC，∠B＝45°，点D、F分别是边BC、AB上的动点，且AF=2BD，以DF为腰向右做等腰△DEF，使得DE＝DF，∠EDF＝45°，连接CE.
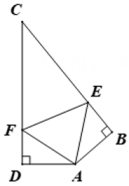
  ①试判断线段DC、BD、BF之间的数量关系，并说明理由；
  ②如图4，已知AC＝2，点G是AC的中点，连接EA，EG，直接写出EA+EG的最小值．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

备考2024年浙江中考数学一轮复习专题19.1三角形（1） ...

副标题：

*注意事项：

备考2024年浙江中考数学一轮复习专题19.1三角形（1） ...

试题分析

总体分析

题量分析

难度分析

知识点分析