观鸟记录年度总结 |
|
|
|
|
|
设小明从年到
年观测鸟类种类数量的年平均增长率为
, 则下列方程正确的是( )

拉力/N | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
弹簧长度/cm | 10.0 | 12.0 | 14.0 | 16.0 | 18.0 | 20.0 | 22.0 |
|
组别 |
花生种子萌发量 |
||||
|
第 |
第 |
第 |
第 |
第 |
|
|
浸种 |
|
|
|
|
|
在温度的条件下,将
粒种子浸种
小时,萌发量大致为 粒


设有编号为1-100的100盏灯,分别对应着编号为1-100的100个开关,灯分为“亮”和“不亮”两种状态,每按一次开关改变一次相对应编号的灯的状态,所有灯的初始状态为“不亮”.现有100个人,第1个人把所有编号是1的整数倍的开关按一次,第2个人把所有编号是2的整数倍的开关按一次,第3个人把所有编号是3的整数倍的开关按一次,……,第100个人把所有编号是100的整数倍的开关按一次.问最终状态为“亮”
的灯共有多少盏?
几位同学对该问题展开了讨论:
甲:应分析每个开关被按的次数找出规律:
乙:1号开关只被第1个人按了1次,2号开关被第1个人和第2个人共按了2次,3号开关被第1个人和第3个人共按了2次,……
丙:只有按了奇数次的开关所对应的灯最终是“亮”的状态.
根据以上同学的思维过程,可以得出最终状态为“亮”的灯共有盏.

【步骤一】设计测量方案:小组成员讨论后,画出如图①的测量草图,确定需测的几何量.
【步骤二】准备测量工具:皮尺和自制测高仪.其中测高仪(如图②)为正方形木板,在顶点
处用细线挂一个铅锤
.
【步骤三】实地测量并记录数据:如图③,令测高仪上的顶点 ,
与“摇橹人”最高点
在同一条直线上.通过测量得到,
,
,
.
【步骤四】计算“摇橹人”高度.(结果精确到0.1m)(参考数据:
,
,
)
现在,请你结合图③和相关数据完成【步骤四】.
如图2,在坡角点C处测得旗杆顶点A的仰角的正切值为2,山坡上点D处测得顶点A的仰角
的正切值为
, 斜坡
的坡比为
, 两观测点
的距离为
.
学习小组成员对问题进行如下分解,请探索并完成任务.
①计算C,D两点的垂直高度差.
②求顶点A到水平地面的垂直高度.
为了计算得到旗杆的高度,两个小组在共同解决任务1和2后,采取了不同的方案:
小组一:在坡角点C处测得旗杆底部点B的仰角的正切值为
;
小组二:在山坡上点D处测得旗杆底部点B的俯角的正切值为
.
请选择其中一个小组的方案计算旗杆的高度.
水火箭是一种基于水和压缩空气的简易火箭,通常由塑胶汽水瓶作为火箭的箭身,并把水当作喷射剂.图1是某学校兴趣小组制做出的一款简易弹射水火箭.

【实验操作】
为验证水火箭的一些性能,兴趣小组同学通过测试收集了水火箭相对于出发点的水平距离(单位:
)与飞行时间
(单位:
)的数据,并确定了函数表达式为:
.同时也收集了飞行高度
(单位:
)与飞行时间
(单位:
)的数据,发现其近似满足二次函数关系.数据如表所示:
飞行时间 | 0 | 2 | 4 | 6 | 8 | … |
飞行高度 | 0 | 10 | 16 | 18 | 16 | … |
求关于
的函数表达式.
图2是兴趣小组同学在室内操场的水平地面上设置一个高度可以变化的发射平台(距离地面的高度为),当弹射高度变化时,水火箭飞行的轨迹可视为抛物线上下平移得到,线段
为水火箭回收区域,已知
,
.
探究飞行距离,当水火箭落地(高度为)时,求水火箭飞行的水平距离.
主题:制作圆锥形生日帽.
素材:一张圆形纸板、装饰彩带.
步骤1:如图1,将一个底面半径为r的圆锥侧面展开,可得到一个半径为l、圆心角为的扇形.制作圆锥形生日帽时,要先确定扇形的圆心角度数,再度量裁剪材料.
步骤2:如图2,把剪好的纸板粘合成圆锥形生日帽.
在制作好的生日帽中, ,
, C是
的中点,现要从点A到点C再到点A之间拉一条装饰彩带,求彩带长度的最小值.

如何调整足球的发球方向 | ||
素材1 | 如图是某足球场的一部分,球门宽DE=CF=7m,高CD=EF=2.5m,小梅站在A处向门柱CD一侧发球,点A正对门柱CD(即AC⊥CF),AC=24m,足球运动的路线是抛物线的一部分. |
|
素材2 | 如图,当足球运动到最高点 |
|
素材3 | 距离球门正前方6m处放置一块矩形拦网HGMN,拦网面垂直于地面,且GH∥CF,拦网高HN=4m. |
|
问题解决 | ||
任务1 | 结合素材1,2,求足球运动的高度 | |
任务2 | 结合素材1,2,小梅不改变发球的方向,射门路线的形状和最大高度保持不变此时足球能否进入球门?若不能进入,他应该带球向正后方至少移动多少米射门才能让足球进入球门 | |
任务3 | 结合以上素材,小梅站在A处,只改变发球方向,射门路线的形状和最大高度保持不变,请探求此时足球能否越过拦网,在点E处进入球门 | |
上述任务1、任务2、任务3中球落在门柱边线视同足球进入球门 | ||
【问题情境】某校兴趣小组在老师的指导下对一批花卉种子进行了人工培育,并针对这批种子的发芽率进行实践探究.
【实践发现】兴趣小组将不同数量种子的发芽数进行统计,并计算出发芽率,整理数据如下表所示:
种子数m | 40 | 90 | 140 | 220 | 490 | 900 | 1200 | 2400 |
发芽数n | 36 | 84 | 123 | 196 | 439 | 805 | 1092 | 2154 |
发芽率 | 0.90 | 0.93 | 0.88 | 0.89 | 0.90 | 0.89 | 0.91 | 0.90 |
【实践探究】分析数据如下:
| 平均数 | 众数 | 中位数 |
发芽率 | 0.90 | a | b |
【问题解决】
实验环境一 无光照(其余条件与之前均相同) | ||
种子数量(颗) | 发芽数量 | 发芽率 |
500 | 410 | 0.82 |
实验环境二 多次浇水(其余条件与之前均相同) | ||
种子数量(颗) | 发芽数量 | 发芽率 |
500 | 425 | 0.85 |
请结合数据分析,第二批种子的发芽率与设想相差较大的原因(写出一条原因即可).}
杨梅季将至,梅企与某快递公司合作寄送杨梅. | ||||
素材1 | 某快递公司规定:(1)从当地寄送杨梅到 (2)寄送杨梅重量均为整数千克. | |||
素材2 |
|
|
| |
并写出一种寄送方式.
项目主题:从函数角度重新认识“阻力对物体运动的影响”.
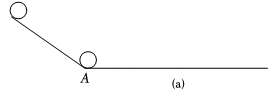
项目内容:数学兴趣小组对一个静止的小球从斜坡滚下后,在水平木板上运动的速度、距离与时间的关系进行了深入探究,兴趣小组先设计方案,再进行测量,然后根据所测量的数据进行分析,并进一步应用。
实验过程:如图(a)所示,一个黑球从斜坡顶端由静止滚下沿水平木板直线运动,从黑球运动到点A处开始,用频闪照相机、测速仪测量并记录黑球在木板上的运动时间x(单位:s)、运动速度v(单位:cm/s)、滑行距离y(单位:cm)的数据.
任务一:数据收集
记录的数据如下:
运动时间x/s | 0 | 2 | 4 | 6 | 8 | 10 | … |
运动速度v/(cm/s) | 10 | 9 | 8 | 7 | 6 | 5 | … |
滑行距离y/cm | 0 | 19 | 36 | 51 | 64 | 75 | … |
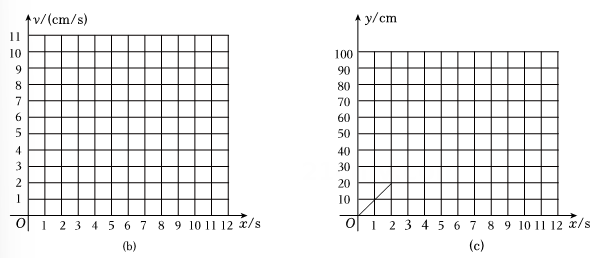
根据表格中的数值分别在图(b)、图(c)中作出v与x的函数图象、y与x的函数图象:
情景:图1是一直角过道示意图,O,P为直角顶点,过道宽度都是1.2m.矩形ABCD是某物品经过该过道时的俯视图,宽AB为0.8m.

操作:
步骤 | 动作 | 目标 |
1 | 靠边 | 将如图1中矩形ABCD的一边AD靠在SO上 |
2 | 推移 | 矩形ABCD沿SO方向推移一定距离,使点O在边AD上 |
3 | 旋转 | 如图2,将矩形ABCD绕点O旋转90° |
4 | 推移 | 将矩形ABCD沿OT方向继续推移 |
探究:
教学实践活动: | ||
活动 | 如图, |
|
活动 | 如图,小组 |
|
总结与取优 | ||
老师做了一个小小的总结,并且设计了一个新的方案,已知塔前有一高 |
| |
车轮设计成圆形的数学道理
小青发现路上行驶的各种车辆,车轮都是圆形的为什么车轮要做成圆形的呢?这里面有什么数学道理吗?带着这样的疑问,小青做了如下的探究活动:
将车轮设计成不同的正多边形,在水平地面上模拟行驶.

优化洒水车为公路两侧绿化带浇水效率 | |||
信息1 | 如图1,洒水车沿着平行于公路路牙方向行驶,喷水口H离地竖直高度OH为1.5m. |
| |
信息2 | 如图2,可以把洒水车喷出水的内、外边缘抽象为平面直角坐标系中两条抛物线的部分图象;把绿化带横截面抽象为矩形DEFG,其水平宽度DE=3m,竖直高度EF=0.5m.内边缘抛物线y2是由外边缘抛物线y1向左平移得到,外边抛物线y1最高点A离喷水口的水平距离为2m,高出喷水口0.5m. | ||
问题解决 | |||
任务1 | 确定浇灌方式 | (1)求外边缘抛物线y1的函数解析式,并求喷出水的最大射程OC; | |
(2)直接写出内边缘抛物线y与x轴的正半轴交点B的坐标; | |||
任务2 | 提倡有效浇灌 | (3)要使洒水车行驶时喷出的水能浇灌到整个绿化带,求OD的取值范围. | |
1 | 1.5 | 2 | 4 | |
3 | 4.5 | 6 | 12 |
