2024年江苏省南京市中考数学仿真模拟卷

更新时间：2024-05-09 浏览次数：171 类型：中考模拟

一、选择题（每题2分，共12分）

1. (2024七上·南宁期中) 风云二号是我国自行研制的第一代地球静止气象卫星，它在地球赤道上空距地面约35800公里的轨道上运行．将35800用科学记数法表示应为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024八下·沙洋期中) 估计 $\text{[math]}$ 的值在

A . 2到3之间 B . 3到4之间 C . 4到5之间 D . 5到6之间

答案解析收藏纠错 + 选题
3. (2021九上·霍林郭勒期末) 如图，若干全等正五边形排成形状，图中所示的是前3个正五边形，则要完成这一圆环还需这样的正五边形（）

A . 6个 B . 7个 C . 9个 D . 10个

答案解析收藏纠错 + 选题
4. (2024·黔南模拟) 二次函数 $\text{[math]}$ 的顶点在第几象限（）

A . 一 B . 二 C . 三 D . 四

答案解析收藏纠错 + 选题
5. 如图，小聪用图1中的一副七巧板拼出如图2所示“鸟”，已知正方形ABCD的边长为4，则图2中E，F两点之间的距离为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024·金华模拟) 如图，四个全等的直角三角形排成“赵爽弦图”，其中四边形ABCD与四边形EFGH都是正方形.连结DG并延长，交BC于点 $\text{[math]}$ ，点 $\text{[math]}$ 为BC的中点.若 $\text{[math]}$ ，则AE的长为（）

A . 4 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（每题2分，共20分）

7. (2024·江汉模拟) 写出一个比4小的正无理数．

答案解析收藏纠错 + 选题
8. (2024九下·昆明开学考) 要使式子 $\text{[math]}$ 有意义，x的取值范围是．

答案解析收藏纠错 + 选题
9. (2024九下·杭州模拟) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
10. (2024九下·盱眙模拟) 若一元二次方程x²＋x－c＝0没有实数根，则c的取值范围是．

答案解析收藏纠错 + 选题
11. (2024七下·桂林月考) 规定两数a、b之间的一种运算，记作 $\text{[math]}$ ：如果 $\text{[math]}$ ，那么 $\text{[math]}$ ．例如：因为 $\text{[math]}$ ，所以 $\text{[math]}$ ．根据上述规定，填空：若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
12. (2024九下·凉州模拟) 已知样本x₁ ， x₂ ， …x_n的平均数是5，方差是3，则样本3x₁+5，3x₂+5，…3x_n+5的方差是．

答案解析收藏纠错 + 选题
13. (2023·肇东模拟) 甲计划用若干个工作日完成某项工作，从第三个工作日起，乙加入此项工作，且甲乙两人工效率相同，结果提前 $\text{[math]}$ 天完成任务，则甲计划完成此项工作的天数是．

答案解析收藏纠错 + 选题
14. (2024九下·永昌模拟) 已知点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在反比例函数 $\text{[math]}$ 的图象上，且 $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的大小关系是．

答案解析收藏纠错 + 选题
15. (2024·南山模拟) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的弦， $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 相切， $\text{[math]}$ ， $\text{[math]}$ 相交于点 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则线段 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题
16. (2024·贵州模拟) 如图，在平面直角坐标系中，点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的坐标分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 是三角形 $\text{[math]}$ 的外接圆 $\text{[math]}$ 上一点， $\text{[math]}$ 交线段 $\text{[math]}$ 于点 $\text{[math]}$ ，若 $\text{[math]}$ ，则点 $\text{[math]}$ 的坐标为.

答案解析收藏纠错 + 选题

三、解答题（共11题，共88分）

17. (2024·南京二模) 解不等式 $\text{[math]}$ ，并把它的解集在数轴上表示出来．

答案解析收藏纠错 + 选题
18. (2023·红花岗模拟) 小红在计算 $\text{[math]}$ 时，解答过程如下：
原式 $\text{[math]}$
$\text{[math]}$
$\text{[math]}$
1. （1）小红的解答从第步开始出错；
2. （2）请写出正确的解答过程．
答案解析收藏纠错 + 选题
19. (2024·江汉模拟) 如图，点D ， E ， F分别是 $\text{[math]}$ 的边 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 上的点， $\text{[math]}$ ， $\text{[math]}$ ，
1. （1）求证：四边形 $\text{[math]}$ 为平行四边形；
2. （2）若 $\text{[math]}$ ，直接写出 $\text{[math]}$ 的值为．
答案解析收藏纠错 + 选题
20. (2024九下·齐齐哈尔开学考) 今年4月 $\text{[math]}$ 日是我国第八个“全民国家安全教育日”．为增强学生国家安全意识，夯实国家安全教育基础、某市举行国家安全知识竞赛．竞赛结束后，发现所有参赛学生的成绩（满分 $\text{[math]}$ 分）均不低于 $\text{[math]}$ 分．小明将自己所在班级学生的成绩（用x表示）分为四组：A组（ $\text{[math]}$ ），B组（ $\text{[math]}$ ），C组（ $\text{[math]}$ ），D组（ $\text{[math]}$ ），绘制了如图不完整的频数分布直方图和扇形统计图．
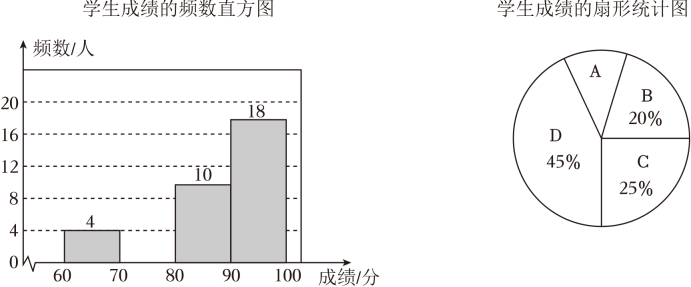
根据以上信息，解答下列问题：
1. （1）补全频数分布直方图；
2. （2）扇形统计图中A组所对应的圆心角的度数为 $\text{[math]}$ ；
3. （3）把每组中各个同学的成绩用这组数据的中间值（如A组： $\text{[math]}$ 的中间值为 $\text{[math]}$ ）来代替，试估计小明班级的平均成绩；
4. （4）小明根据本班成绩，估计全市参加竞赛的所有 $\text{[math]}$ 名学生中会有 $\text{[math]}$ 名学生成绩低于 $\text{[math]}$ 分，实际只有 $\text{[math]}$ 名学生的成绩低于 $\text{[math]}$ 分．请你分析小明估计不准确的原因．
答案解析收藏纠错 + 选题
21. (2024·长春模拟) 如图，两个相同的可以自由转动的转盘A和B ，转盘A被三等分，分别标有数字6，2，1；转盘B被四等分，分别标有数字 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .（当指针指在两个扇形的交线时，需重新转动转盘）
1. （1）转动转盘B一次，转盘停止时，指针指向偶数的概率为；
2. （2）同时转动两个转盘，转盘停止时，求两个指针指向的数字之和大于0的概率.（画树状图或列表法）
答案解析收藏纠错 + 选题
22. (2024·中山模拟) 某商家销售某种商品，每件进价为40元．经市场调查发现，该商品一周的销售量y（大于0的整数）件与销售单价x（不低于50的整数）满足一次函数关系，部分调查数据如表：
销售单价x（元/件）
50
55
60
70
75
…
一周的销售量y（件）
500
450
400
300
250
…
1. （1）直接写出销售量y关于销售单价x的函数表达式：y＝．
2. （2）若一周的销售利润为2750元，则销售单价是多少元/件？
3. （3）现商家决定将商品一周的销售利润作为捐款寄往贫困地区，则捐款能达到的最大值是元．
答案解析收藏纠错 + 选题
23. (2023·偃师模拟)
1. （1）【基础巩固】如图1，在 $\text{[math]}$ 中，D，E，F分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 上的点， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于点G，求证： $\text{[math]}$ .
2. （2）【尝试应用】如图2，在（1）的条件下，连接 $\text{[math]}$ ， $\text{[math]}$ .若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的值.
3. （3）【拓展提高】如图3，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 交于点O，E为 $\text{[math]}$ 上一点， $\text{[math]}$ 交 $\text{[math]}$ 于点G， $\text{[math]}$ 交 $\text{[math]}$ 于点F.若 $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
24. (2024·南京二模) 筒车是我国古代利用水力驱动的灌溉工具，如图，半径为3m的筒车⊙O按逆时针方向每分钟转 $\text{[math]}$ 圈，筒车与水面分别交于点A、B ，筒车的轴心O距离水面的高度OC为2.2m ，筒车上均匀分布着若干个盛水筒，若以某个盛水筒P刚浮出水面（点A）时开始计算时间．
1. （1）求盛水筒P从A点到达最高点所经过的路程；
2. （2）求浮出水面3.4秒时，盛水筒P到水面的距离；
3. （3）若接水槽MN所在直线是⊙O的切线，且与直线AB交于点M ， MO＝8m ，直接写出盛水筒P从最高点开始，经过多长时间恰好第一次落在直线MN上．（参考数据：cos43°＝sin47°≈ $\text{[math]}$ ， sin16°＝cos74°≈ $\text{[math]}$ ， sin22°＝cos68°≈ $\text{[math]}$ ）
答案解析收藏纠错 + 选题

25. (2024·威远模拟) 阅读与应用

我们知道 $\text{[math]}$ ，即 $\text{[math]}$ ，所以 $\text{[math]}$ （当且仅当 $\text{[math]}$ 时取等号）.

阅读1：若 $\text{[math]}$ 为实数，

且 $\text{[math]}$ ，

$\text{[math]}$

$\text{[math]}$ （当且仅当 $\text{[math]}$ 时取等号）

阅读2：若函数 $\text{[math]}$ （ $\text{[math]}$ 为常数），

$\text{[math]}$ ，

由阅读1的结论可知 $\text{[math]}$ ，即 $\text{[math]}$

$\text{[math]}$ 当 $\text{[math]}$ 时，函数 $\text{[math]}$ 有最小值，最小值为 $\text{[math]}$ .

阅读理解以上材料，解答下列问题：

（1）当 $\text{[math]}$ 时，函数 $\text{[math]}$ 有最小值，最小值为.
（2）疫情防控期间，某核酸检测采样点用隔离带分区管理，如图是一边靠墙其它三边用隔离带围成的面积为 $\text{[math]}$ 的矩形隔离区域，假设墙足够长，则这个矩形隔离区域的长和宽分别是多少时，所用隔离带的长度最短？
（3）随着高科技赋能传统快递行业，某大型物流公司为提高工作效率引进一批分拣机器人，已知每台机器人的运营成本包含以下三个部分：一是进价为25000元；二是材料损耗费，每小时为7元；三是折旧费，折旧费y（元）与运营工作时间t（小时）的函数关系式为 $\text{[math]}$ .当运营工作时间t长达多少小时时，每台机器人平均每小时的运营成本最低？最低运营成本是多少？

答案解析收藏纠错 + 选题

26. (2024·雅安模拟) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的直径，点 $\text{[math]}$ 在 $\text{[math]}$ 上， $\text{[math]}$ 平分 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 的垂线交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线；
2. （2）求证： $\text{[math]}$
3. （3）若 $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
27. (2024·南京二模) 定义：点P（m ， m）是平面直角坐标系内一点，将函数l的图象位于直线x＝m左侧部分，以直线y＝m为对称轴翻折，得到新的函数l^'的图象，我们称函数l^'的函数是函数l的相关函数，函数l^'的图象记作F₁ ，函数l的图象未翻折的部分记作F₂ ，图象F₁和F₂合起来记作图象F ．
例如：函数l的解析式为y＝x²﹣1，当m＝1时，它的相关函数l^'的解析式为y＝﹣x²+3（x＜1）．
1. （1）如图，函数l的解析式为y＝﹣ $\text{[math]}$ x+2，当m＝﹣1时，它的相关函数l^'的解析式为y＝．
2. （2）函数l的解析式为y＝﹣ $\text{[math]}$ ，当m＝0时，图象F上某点的纵坐标为﹣2，求该点的横坐标．
3. （3）已知函数l的解析式为y＝x²﹣4x+3，
  ①已知点A、B的坐标分别为（0，2）、（6，2），图象F与线段AB只有一个公共点时，结合函数图象，求m的取值范围；
  ②若点C（x ， n）是图象F上任意一点，当m﹣2≤x≤5时，n的最小值始终保持不变，求m的取值范围（直接写出结果）．
答案解析收藏纠错 + 选题