【培优版】2024-2025学年浙教版数学九上1.3二次函数...

更新时间：2024-07-24 浏览次数：33 类型：同步测试

一、选择题

1. (2024·达州) 抛物线y＝﹣x²+bx+c与x轴交于两点，其中一个交点的横坐标大于1，另一个交点的横坐标小于1，则下列结论正确的是（　　）

A . b+c＞1 B . b＝2 C . b²+4c＜0 D . c＜0

答案解析收藏纠错 + 选题
2. (2024·新昌模拟) 已知二次函数y＝ax²＋bx＋c（a≠0），当y＜n时，x的取值范围是t－3＜x＜1－t ，且该二次函数的图象经过点M（3，m²＋3），N（d ， 2m）两点，则d的值不可能是（）

A . －3 B . －1 C . 2 D . 4

答案解析收藏纠错 + 选题
3. (2024·惠城模拟) 如图所示，抛物线 $\text{[math]}$ 经过矩形ABCD的三个顶点A ， B ， D，则点C的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024·滨江二模) 已知二次函数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．当 $\text{[math]}$ 时，该函数有最大值 $\text{[math]}$ 和最小值 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 有最大值 $\text{[math]}$ B . 无最大值 C . 有最小值 $\text{[math]}$ D . 无最小值

答案解析收藏纠错 + 选题
5. (2019九上·凤山期中) 设一元二次方程 $\text{[math]}$ 的两根分别为 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$
满足（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$ 且 $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024·南充模拟) 如图，抛物线 $\text{[math]}$ 与x轴交于点A(－6，0)．点 $\text{[math]}$ ， $\text{[math]}$ 是抛物线上两点，当t≤x≤t＋3时，二次函数最大值记为 $\text{[math]}$ ，最小值记为 $\text{[math]}$ ，设 $\text{[math]}$ ，则m的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024九上·青县期末) 如图，把二次函数 $\text{[math]}$ 的图象在x轴上方的部分沿着x轴翻折，得到的新函数叫做 $\text{[math]}$ 的“陷阱”函数．小明同学画出了 $\text{[math]}$ 的“陷阱”函数的图象，如图所示并写出了关于该函数的4个结论，其中正确结论的个数为（）
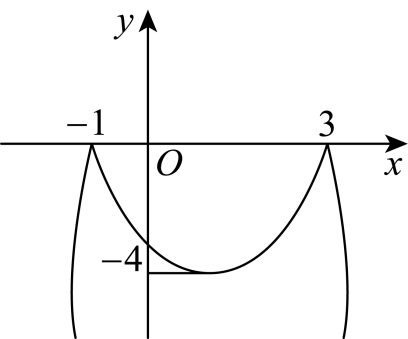
①图象具有对称性，对称轴是直线 $\text{[math]}$ ； ②由图象得 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；③该“陷阱”函数与y轴交点坐标为 $\text{[math]}$ ；④ $\text{[math]}$ 的“陷阱”函数与 $\text{[math]}$ 的“陷阱”函数的图象是完全相同的．

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
8. (2024九上·祁东期末) 二次函数 $\text{[math]}$ 的顶点坐标为 $\text{[math]}$ ，其部分图象如图所示，下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ③若点 $\text{[math]}$ ，点 $\text{[math]}$ 是函数图象上的两点，则 $\text{[math]}$ ；④关于x的方程 $\text{[math]}$ 无实数根；其中正确结论有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题

9. (2023九上·期中) 已知二次函数 $\text{[math]}$ （m为常数）的图象与x轴有交点，且当x＜-3时，y随x的增大而增大，则m的取值范围是

答案解析收藏纠错 + 选题
10. (2023九上·杭州开学考) 如图，在 $\text{[math]}$ 纸片中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ 分别在 $\text{[math]}$ 、 $\text{[math]}$ 边上，连接 $\text{[math]}$ ，将 $\text{[math]}$ 沿 $\text{[math]}$ 翻折，使点 $\text{[math]}$ 落在点 $\text{[math]}$ 的位置，且四边形 $\text{[math]}$ 是菱形．
1. （1）若点 $\text{[math]}$ 在 $\text{[math]}$ 边上时，则菱形 $\text{[math]}$ 的边长为；
2. （2）连接 $\text{[math]}$ ，则 $\text{[math]}$ 的长的最小值为．
答案解析收藏纠错 + 选题
11. (2023八下·南通期末) 如图，在正方形ABCD中， $\text{[math]}$ ，点E为对角线AC上的动点，以DE为边作正方形DEFG．点H是CD上一点，且 $\text{[math]}$ ，连接GH，则GH的最小值为．

答案解析收藏纠错 + 选题
12. (2023·白碱滩模拟) 如图是抛物线 $\text{[math]}$ 图象的一部分，抛物线的顶点坐标为 $\text{[math]}$ ，与x轴的一个交点为 $\text{[math]}$ ，点A和点B均在直线 $\text{[math]}$ 上．① $\text{[math]}$ ；② $\text{[math]}$ ；③抛物线与x轴的另一个交点为 $\text{[math]}$ ；④方程 $\text{[math]}$ 有两个不相等的实数根；⑤不等式 $\text{[math]}$ 的解集为 $\text{[math]}$ ．上述五个结论中，其中正确的结论是（填写序号即可）．

答案解析收藏纠错 + 选题

三、综合题

13. (2021·镇海模拟) 如图，在一次足球比赛中，守门员在地面 $\text{[math]}$ 处将球踢出，一运动员在离守门员8米的 $\text{[math]}$ 处发现球在自己头上的正上方4米处达到最高点 $\text{[math]}$ ，球落地后又一次弹起.据实验测算，足球在空中运行的路线是一条抛物线，在草坪上弹起后的抛物线与原来的抛物线形状相同，最大高度减少到原来最大高度的一半.
1. （1）求足球第一次落地之前的运动路线的函数表达式及第一次落地点 $\text{[math]}$ 和守门员（点 $\text{[math]}$ ）的距离；
2. （2）运动员（点 $\text{[math]}$ ）要抢到第二个落点 $\text{[math]}$ ，他应再向前跑多少米？（假设点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 在同一条直线上，结果保留根号）
答案解析收藏纠错 + 选题
14. (2021九上·台山期末) 如图，二次函数 $\text{[math]}$ 的图象与x轴交于A、B两点（点A在点B的右侧），与y轴交于点C．
1. （1）求点A、B、C的坐标；
2. （2）若点M在抛物线的对称轴上，且△MAC的周长最小，求点M的坐标；
3. （3）若点P在x轴上，且△PBC为等腰三角形，请求出所有符合条件的点P的坐标．
答案解析收藏纠错 + 选题
15. (2023·南充) 如图1，抛物线 $\text{[math]}$ （ $\text{[math]}$ ）与 $\text{[math]}$ 轴交于 $\text{[math]}$ ， $\text{[math]}$ 两点，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ．
1. （1）求抛物线的解析式；
2. （2）点P在抛物线上，点Q在x轴上，以B，C，P，Q为顶点的四边形为平行四边形，求点P的坐标；
3. （3）如图2，抛物线顶点为D，对称轴与x轴交于点E，过点 $\text{[math]}$ 的直线（直线 $\text{[math]}$ 除外）与抛物线交于G，H两点，直线 $\text{[math]}$ ， $\text{[math]}$ 分别交x轴于点M，N．试探究 $\text{[math]}$ 是否为定值，若是，求出该定值；若不是，说明理由．
答案解析收藏纠错 + 选题

四、实践探究题

16. 定义：若两个二次函数 $\text{[math]}$ 的图象关于 $\text{[math]}$ 轴对称，则称 $\text{[math]}$ 互为“对称二次函数”.
1. （1）已知二次函数 $\text{[math]}$ ，则它的“对称二次函数”的顶点坐标为.
2. （2）已知关于 $\text{[math]}$ 的二次函数 $\text{[math]}$ 和 $\text{[math]}$ ，其中 $\text{[math]}$ 的图象经过点 $\text{[math]}$ .若 $\text{[math]}$ 与 $\text{[math]}$ 互为“对称二次函数”，求函数 $\text{[math]}$ 的表达式；
3. （3）在(2)的条件下，当 $\text{[math]}$ 时， $\text{[math]}$ 的最小值为-2，请直接写出 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
17. (2023九上·南关月考) 法国数学家韦达在研究一元二次方程时发现：如果关于x的一元二次方程 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ）的两个实数根分别为 $\text{[math]}$ 、 $\text{[math]}$ ，那么 $\text{[math]}$ ， $\text{[math]}$ ．习惯上把这个结论称作“韦达定理”．
1. （1）方程 $\text{[math]}$ 的两个实数根分别为 $\text{[math]}$ 、 $\text{[math]}$ ，求 $\text{[math]}$ 和 $\text{[math]}$ 的值．
2. （2）方程 $\text{[math]}$ 的两个实数根分别为 $\text{[math]}$ 、 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
3. （3）若 $\text{[math]}$ 、 $\text{[math]}$ 为关于x的方程 $\text{[math]}$ 的两个实数根，求 $\text{[math]}$ 的最小值．
答案解析收藏纠错 + 选题

18. 根据以下素材，探索完成任务。

运用二次函数研究电缆架设问题
素材1	电缆在空中架设时，两端挂起的电缆下垂都可以近似地看成抛物线的形状.如图，在一个斜坡 BD上按水平距离间隔90m架设两个塔柱，每个塔柱固定电缆的位置离地面高度为20m（AB=CD=20m），按如图所示的方式建立平面直角坐标系（x轴在水平方向上）.点A，O，E 在同一水平线上，经测量，AO=60m，斜坡BD的坡比为1：10.
素材2	若电缆下垂的安全高度是13.5m，即电缆距离坡面铅直高度的最小值不小于13.5m时，符合安全要求，否则存在安全隐患. （说明：直线GH⊥x轴且分别与直线BD和抛物线相交于点H，G.点G 距离坡面的铅直高度为GH 的长）
任务1	确定电缆形状	求点 D 的坐标及下垂电缆的抛物线的函数表达式.
任务2	判断电缆安全	上述这种电缆的架设是否符合安全要求？请说明理由.
任务3	探究安装方法	工程队想在坡比为1：8的斜坡上架设电缆，两个塔柱的高度仍为20m，电缆抛物线的形状与任务1相同.若电缆下垂恰好符合安全高度要求，则两个塔柱的水平距离应为多少米？

答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

【培优版】2024-2025学年浙教版数学九上1.3二次函数...

副标题：

*注意事项：

【培优版】2024-2025学年浙教版数学九上1.3二次函数...

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析