浙教版数学九上第2章简单事件的概率一阶单元测试卷

更新时间：2024-07-31 浏览次数：2 类型：单元试卷

一、选择题（本题有10小题，每小题3分，共30分）

1. (2024七下·顺德期末) 下列事件中，必然事件是（）

A . 早晨的太阳从西方升起 B . 任意买一张电影票，座位号是2的倍数 C . 从地面向上抛出的篮球会落下 D . 任意掷一个矿泉水瓶盖，盖口向上

答案解析收藏纠错 + 选题
2. (2024九下·杭州模拟) 将分别标有数字2，3，x的三个球放入不透明的袋中，这些球除所标的数字外都相同，搅匀后任意摸出一个球．若摸出球上的数字小于7是必然事件，则x的值可以是（）

A . 11 B . 9 C . 7 D . 5

答案解析收藏纠错 + 选题
3. (2024·嘉兴模拟) 学校组织研学活动，安排给九年级三辆车，小明与小慧都可以从这三辆车中任选一辆搭乘，则小明与小慧同车的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024·津市市模拟) “明天下雨的概率为 $\text{[math]}$ ”，下列对这句话的理解正确的是（）

A . 明天一定下雨 B . 明天一定不下雨 C . 明天80%的地方下雨 D . 明天下雨的可能性很大

答案解析收藏纠错 + 选题
5. (2024·邱县模拟) 用力转动转盘甲和转盘乙的指针，两个转盘的指针停在白色区域的概率分别为P_甲， P_乙，则下列关系正确的是（）

A . P_甲>P_乙 B . P_甲<P_乙 C . P_甲=P_乙 D . 无法确定P_甲， P_乙的大小

答案解析收藏纠错 + 选题
6. (2024·湖州模拟) 下列说法正确的是( )

A . “明天下雨”是不可能事件 B . 为了解某型号车用电池的使用寿命，采用全面调查的方式 C . 某游戏做 $\text{[math]}$ 次中奖的概率是 $\text{[math]}$ ，那么该游戏连做 $\text{[math]}$ 次就一定会中奖 D . 一组数据 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的中位数是 $\text{[math]}$

答案解析收藏纠错 + 选题

7. (2023·恩施) 县林业部门考察银杏树苗在一定条件下移植的成活率，所统计的银杏树苗移植成活的相关数据如下表所示：

移植的棵数a	100	300	600	1000	7000	15000
成活的棵数b	84	279	505	847	6337	13581
成活的频率 $\text{[math]}$	0.84	0.93	0.842	0.847	0.905	0.905

根据表中的信息，估计银杏树苗在一定条件下移植成活的概率为（精确到0.1）（　　）

A . 0.905 B . 0.90 C . 0.9 D . 0.8

答案解析收藏纠错 + 选题

8. (2024·宣恩模拟) 某条河流的流向（从左往右）及分支如图，其中阴影是A县所在地区，并有两条河流从A县穿过，现有2艘小船从左往右航行，则2艘小船都穿过A县的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024·平江二模) 在如图所示的电路中，随机闭合开关 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 中的两个，能让红灯发光的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024·湖北模拟) 从不透明的袋子中进行摸球游戏，这些球除颜色外其他都相同，小红根据游戏规则，作出如图所示的树状图，则此次摸球的游戏规则是

A . 随机摸出一个球后放回，再随机摸出1个球 B . 随机摸出一个球后不放回，再随机摸出1个球 C . 随机摸出一个球后放回，再随机摸出3个球 D . 随机摸出一个球后不放回，再随机摸出3 个球

答案解析收藏纠错 + 选题

二、填空题（本题有6小题，每小题4分，共24分）

11. (2023七下·七星关期末) 用抽签的办法从 A 、B 、C 、D 四人中任选一人去打扫公共场地，选中 A 的概率是．

答案解析收藏纠错 + 选题
12. (2024·青海) 如图，一只蚂蚁在树枝上寻觅食物，假定蚂蚁在每个叉路口都随机选择一条路径，它获得食物的概率是．

答案解析收藏纠错 + 选题
13. (2023九上·杭州期中) 某学习小组做抛掷一枚瓶盖的实验，整理的实验数据如表：
累计抛掷次数
50
100
200
300
500
1000
2000
3000
5000
盖面朝上次数
28
54
106
158
264
527
1056
1587
2650
盖面朝上频率
0.5600
0.5400
0.5300
0.5267
0.5280
0.5270
0.5280
0.5290
0.530
随着实验次数的增大，“盖面朝上”的概率接近于（精确到0.01）．

答案解析收藏纠错 + 选题
14. (2024·柯桥模拟) 如图，转盘中黄色扇形的圆心角为 $\text{[math]}$ ，绿色扇形的圆心角为 $\text{[math]}$ ，现让转盘自由转动一次，则指针落在黄色区域的概率为．（注：当指针恰好指在分界线上时，无效重转）

答案解析收藏纠错 + 选题
15. (2024·宝安模拟) 如图，A，B，C，D四名选手参加赛跑，赛场共设1，2，3，4四条跑道，选手以随机抽签方式决定各自的跑道，则 $\text{[math]}$ 两位选手抽中相邻跑道的概率为．

答案解析收藏纠错 + 选题
16. (2024九下·双流月考) 如图，AD为 $\text{[math]}$ 的中线，点E，F分别为 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ．现随机向 $\text{[math]}$ 内掷一枚小针，则针尖落在阴影区域的概率为．

答案解析收藏纠错 + 选题

三、解答题（本题共8小题，第17题7分，第18题7分，第19题7分，第20题6分，第21题8分，第22题7分，第23题14分，第24题10分，共66分）

17. (2024·广州) 善于提问是应用人工智能解决问题的重要因素之一．为了解同学们的提问水平，对 $\text{[math]}$ ， $\text{[math]}$ 两组同学进行问卷调查，并根据结果对每名同学的提问水平进行评分，得分情况如下（单位：分）：
$\text{[math]}$ 组
75
78
82
82
84
86
87
88
93
95
$\text{[math]}$ 组
75
77
80
83
85
86
88
88
92
96
1. （1）求 $\text{[math]}$ 组同学得分的中位数和众数；
2. （2）现从 $\text{[math]}$ 、 $\text{[math]}$ 两组得分超过90分的4名同学中随机抽取2名同学参与访谈，求这2名同学恰好来自同一组的概率．
答案解析收藏纠错 + 选题
18. (2024·苏州) 一个不透明的盒子里装有4张书签，分别描绘“春”，“夏”，“秋”，“冬”四个季节，书签除图案外都相同，并将4张书签充分搅匀．
1. （1）若从盒子中任意抽取1张书签，恰好抽到“夏”的概率为；
2. （2）若从盒子中任意抽取2张书签（先抽取1张书签，且这张书签不放回，再抽取1张书签），求抽取的书签恰好1张为“春”，1张为“秋”的概率．（请用画树状图或列表等方法说明理由）
答案解析收藏纠错 + 选题
19. (2024·盐城) 在“重走建军路，致敬新四军”红色研学活动中，学校建议同学们利用周末时间自主到以下三个基地开展研学活动．
A．新四军纪念馆（主馆区）；
B．新四军重建军部旧址（泰山庙）；
C．新四军重建军部纪念塔（大铜马）．
小明和小丽各自随机选择一个基地作为本次研学活动的第一站．
1. （1）小明选择基地A的概率为；
2. （2）用画树状图或列表的方法，求小明和小丽选择相同基地的概率．
答案解析收藏纠错 + 选题
20. 据天气预报，某天A地的降雨概率为20%，B地的降雨概率为50%，这天A地，B地都下雨的概率是多少？请设计一个模拟试验来解决这个问题．要求说明你设计的这个模拟试验的方法、过程，列出频数表，算出相应频率及所求概率．

答案解析收藏纠错 + 选题
21. 问题情境：在数学探究活动中，老师给出了如图的图形及下面三个等式：①AB=AC；②DB=DC；③∠BAD=∠CAD.若以其中两个等式作为已知条件，能否得到余下一个等式成立?解决方案：探究△ABD与△ACD全等.
问题解决：
1. （1）当选择①②作为已知条件时，△ABD与△ACD全等吗?(填“全等”或“不全等”)，理由是
2. （2）当任意选择两个等式作为已知条件时，请用列表或画树状图的方法求△ABD≌△ACD的概率.
答案解析收藏纠错 + 选题
22. (2024九下·高州月考) 化学课上，小红学到：将二氧化碳气体通入澄清石灰水，澄清石灰水就会变浑浊以下为四个常考的实验：
A.高锰酸钾制取氧气： $\text{[math]}$
B.碳酸钙制取二氧化碳： $\text{[math]}$
C.电解水： $\text{[math]}$
D.一氧化碳还原每化 $\text{[math]}$
1. （1）若小红从四个实验中任意选一个实验，实验产生的气体不会使澄清石灰水变浑浊的概率是多少?
2. （2）若小红从四个实验中任意选两个实验，请用列表或树状图的方法求两个实验产生的气体均能使澄清石灰水变浑浊的概率.
答案解析收藏纠错 + 选题
23. (2022·淄博) 某中学积极落实国家“双减”教育政策，决定增设“礼仪”“陶艺”“园艺”“厨艺”及“编程”等五门校本课程以提升课后服务质量，促进学生全面健康发展为优化师资配备，学校面向七年级参与课后服务的部分学生开展了“你选修哪门课程（要求必须选修一门且只能选修一门）？”的随机问卷调查，并根据调查数据绘制了如下两幅不完整的统计图：
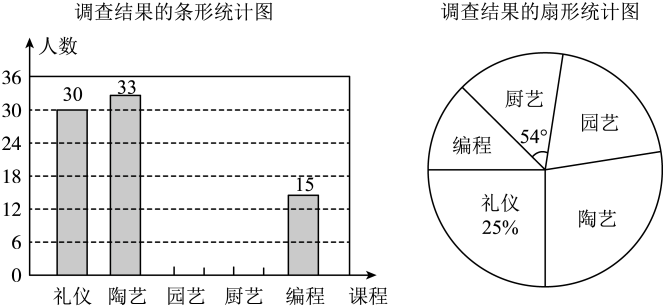
请结合上述信息，解答下列问题：
1. （1）共有名学生参与了本次问卷调查；“陶艺”在扇形统计图中所对应的圆心角是度；
2. （2）补全调查结果条形统计图；
3. （3）小刚和小强分别从“礼仪”等五门校本课程中任选一门，请用列表法或画树状图法求出两人恰好选到同一门课程的概率．
答案解析收藏纠错 + 选题
24. (2022·呼伦贝尔、兴安盟) 一个不透明的口袋中装有四个完全相同的小球，上面分别标有数字1，2，3，4．
1. （1）从口袋中随机摸出一个小球，求摸出小球上的数字是奇数的概率（直接写出结果）；
2. （2）先从口袋中随机摸出一个小球，将小球上的数字记为x，在剩下的三个小球中再随机摸出一个小球，将小球上的数字记为y．请用列表或画树状图法，求由x，y确定的点 $\text{[math]}$ 在函数 $\text{[math]}$ 的图象上的概率．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

浙教版数学九上第2章简单事件的概率一阶单元测试卷

副标题：

*注意事项：

浙教版数学九上第2章简单事件的概率一阶单元测试卷

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析

累计抛掷次数	50	100	200	300	500	1000	2000	3000	5000
盖面朝上次数	28	54	106	158	264	527	1056	1587	2650
盖面朝上频率	0.5600	0.5400	0.5300	0.5267	0.5280	0.5270	0.5280	0.5290	0.530

$\text{[math]}$ 组	75	78	82	82	84	86	87	88	93	95
$\text{[math]}$ 组	75	77	80	83	85	86	88	88	92	96

小学

初中

高中

浙教版数学九上第2章 简单事件的概率 一阶单元测试卷

副标题：

*注意事项：

浙教版数学九上第2章 简单事件的概率 一阶单元测试卷

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析

浙教版数学九上第2章简单事件的概率一阶单元测试卷

浙教版数学九上第2章简单事件的概率一阶单元测试卷