浙教版数学八年级上册《第1章三角形的初步知识》单元同步测试...

更新时间：2024-08-06 浏览次数：89 类型：单元试卷

一、选择题（每题3分，共30分）

1. (2024七下·深圳期中) 下面四个图形中，线段 $\text{[math]}$ 能表示 $\text{[math]}$ 的高的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2024九上·岳阳开学考) 在Rt△ABC中，若一个锐角等于40°，则另一个锐角的度数为（　　）

A . 40° B . 45° C . 50° D . 60°

答案解析收藏纠错 + 选题
3. (2024八上·海曙期末) 已知三角形两边的长分别是3和7，则此三角形第三边的长可能是（）

A . 16 B . 11 C . 3 D . 6

答案解析收藏纠错 + 选题
4. (2024九下·东莞模拟) 下列语句中，不是命题的是（　　）

A . 两点确定一条直线 B . 垂线段最短 C . 作角A的平分线 D . 内错角相等

答案解析收藏纠错 + 选题
5. 如图， $\text{[math]}$ 平分 $\text{[math]}$ ，求证： $\text{[math]}$ $\text{[math]}$ .以下是排乱的证明过程：
① $\text{[math]}$ (已知)，
② $\text{[math]}$ 平分 $\text{[math]}$ (已知)，
③ $\text{[math]}$ (角平分线的定义)，
④ $\text{[math]}$ (两直线平行，同位角相等)，
⑤ $\text{[math]}$ (等量代换).
证明步㵵顺序正确的是（）

A . ③ $\text{[math]}$ ② $\text{[math]}$ ① $\text{[math]}$ ④ $\text{[math]}$ ⑤ B . ① $\text{[math]}$ ④ $\text{[math]}$ ② $\text{[math]}$ ③ $\text{[math]}$ ⑤ C . ① $\text{[math]}$ ③ $\text{[math]}$ ④ $\text{[math]}$ ② $\text{[math]}$ ⑤ D . ① $\text{[math]}$ ④ $\text{[math]}$ ③ $\text{[math]}$ ② $\text{[math]}$ ⑤

答案解析收藏纠错 + 选题
6. (2023八上·东阳月考) 如图，观察图中的尺规作图痕迹，下列说法错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023八上·孝南期末) 已知图中的两个三角形全等，则∠α的度数是（）

A . 72° B . 60° C . 58° D . 50°

答案解析收藏纠错 + 选题
8. (2024八上·石碣期末) 如图，嘉淇利用全等三角形的知识测量池塘两端A，B之间的距离，如果△AOB≌△COD，则只需测出（）

A . OD的长度 B . CD的长度 C . OB的长度 D . AC的长度

答案解析收藏纠错 + 选题
9. (2024八下·腾冲开学考) 如图，已知 $\text{[math]}$ ，再添加一个条件仍不能判定 $\text{[math]}$ 的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023八上·江城期中) 如图，在△ABC中，AB=4，AC=5，以点A为圆心，任意长为半径画弧，分别交AB，AC于点D和E，再分别以点D，E为圆心，大于 $\text{[math]}$ DE长为半径画弧，两弧交于点F，连接AF并延长交BC于点M，作MN⊥AC于点N．若MN=2，则△ABM的面积为（）

A . 4 B . 5 C . 8 D . 10

答案解析收藏纠错 + 选题

二、填空题（每题3分，共18分）

11. (2024八上·浑江期末) 等腰三角形的一边长等于4，一边长等于9，它的周长是.

答案解析收藏纠错 + 选题
12. (2024七下·巴楚月考) 将命题“对顶角相等”改写成“如果……，那么……”的形式：.

答案解析收藏纠错 + 选题
13. (2023八上·团风期中) 如图，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长是．

答案解析收藏纠错 + 选题
14. (2024七下·南海期中) 如图，电线杆上的横梁下方用三角形的支架支撑的理论根据是.

答案解析收藏纠错 + 选题
15. (2024·荆州模拟) 已知： $\text{[math]}$ ．求作： $\text{[math]}$ 的平分线．
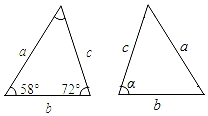
作法：（1）以点 $\text{[math]}$ 为圆心，适当长为半径画弧，交 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ；（2）分别以点 $\text{[math]}$ ， $\text{[math]}$ 为圆心，大于 $\text{[math]}$ 的长为半径画弧，两弧在 $\text{[math]}$ 的内部相交于点 $\text{[math]}$ ；（3）画射线 $\text{[math]}$ ，射线 $\text{[math]}$ 即为所求（如图）．
从上述作法中可以判断 $\text{[math]}$ ，其依据是（在“SSS”“SAS”“AAS”“ASA”中选填）

答案解析收藏纠错 + 选题
16. (2023八上·诸暨月考) 如图，①在OA、OB上分别截取线段OD、OE ，使OD=OE；②分别以 $\text{[math]}$ 为圆心，大于 $\text{[math]}$ 的长为半径画弧，在 $\text{[math]}$ 内两弧交于点 $\text{[math]}$ ；③作射线 $\text{[math]}$ ．若∠AOB=60° ，则 $\text{[math]}$ $\text{[math]}$ ．

答案解析收藏纠错 + 选题

三、解答题（共9题，共72分）

17. (2024八上·福田期末) 已知：如图， $\text{[math]}$ ， $\text{[math]}$ 和 $\text{[math]}$ 相交于点 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 上一点， $\text{[math]}$ 是 $\text{[math]}$ 上一点，
且 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题
18. (2021·苏州模拟) 已知：如图，点A、B、C、D在一条直线上， $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数.
答案解析收藏纠错 + 选题
19. (2021八上·高安期中) 如图，在△ABC中，∠B=∠C，过BC的中点D作DE⊥AB，DF⊥AC，垂足分别为点E、F.
1. （1）求证∶DE=DF；
2. （2）若∠BDE=55°，求∠BAC的度数.
答案解析收藏纠错 + 选题
20. (2021八上·衢州期中) 如图，已知△ABF≌△CDE.
1. （1）若∠B＝30°，∠DCF＝40°，求∠EFC的度数；
2. （2）若BD=10，EF=2，求BF的长.
答案解析收藏纠错 + 选题
21. (2020·阳新模拟) 如图， $\text{[math]}$ 和 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，AB，DE相交于点F，AD，BC相交于点G.
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求DG的长.
答案解析收藏纠错 + 选题
22. (2022八下·凤县期中) 如图，在Rt△ABC中，∠ACB=90°，∠A=40°，△ABC的外角∠CBD的平分线BE交AC的延长线于点E．
1. （1）求∠CBE的度数；
2. （2）过点D作DF∥BE，交AC的延长线于点F，求∠F的度数．
答案解析收藏纠错 + 选题
23. (2022·珠海模拟) 如图，在Rt△ABC中，∠C=90°.
1. （1）作∠BAC的平分线AD交边BC于点D.（尺规作图，保留作图痕迹，不写作法）.
2. （2）在（1）的条件下，若∠BAC=28°，求∠ADB的度数.
答案解析收藏纠错 + 选题
24. (2023八上·黄陂期中) 在 $\text{[math]}$ 中， $\text{[math]}$ ，过直角顶点 $\text{[math]}$ 作直线 $\text{[math]}$ 于点 $\text{[math]}$ 于点 $\text{[math]}$ ．
1. （1）如图1，当 $\text{[math]}$ 与 $\text{[math]}$ 边不相交时，判断 $\text{[math]}$ 之间的数量关系，并说明理由；
2. （2）当 $\text{[math]}$ 与边 $\text{[math]}$ 相交时，请在图2中画出图形，并直接写出 $\text{[math]}$ 之间的数量关系．
答案解析收藏纠错 + 选题
25. (2023八上·江城期中) [问题情境]
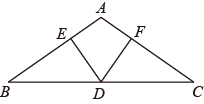
在综合实践课上，老师组织班上的同学开展了探究两角之间数量关系的数学活动，如题24图，已知射线AM∥BN，连接AB，点P是射线AM上的一个动点(与点A不重合)，BC，BD分别平分∠ABP和∠PBN，且分别交射线AM于点C，D．
[探索发现]
1. （1）当∠A=60°时，求证：∠CBD=∠A．
2. （2） ”快乐小组”经过探索后发现：不断改变∠A的度数，∠CBD与∠A始终存在某种数量关系．
  ①当∠A=40°时，∠CBD=度；
  ②当∠A=x°时，∠CBD=度(用含x的代数式表示)．
3. （3） [操作探究]
  ”智慧小组”利用量角器量出∠APB和∠ADB的度数后，探究二者之间的数量关系．他们惊奇地发现，当点P在射线AM上运动时，无论点P在AM上的什么位置，∠APB与∠ADB之间的数量关系都保持不变．请写出它们的关系，并说明理由．
答案解析收藏纠错 + 选题