浙教版数学九年级上册《第2章简单事件的概率》单元提升测试卷

更新时间：2024-08-08 浏览次数：7 类型：单元试卷

一、选择题（每题3分，共30分）

1. (2024·兴安盟、呼伦贝尔) 下列说法正确的是( )

A . 任意画一个三角形，其内角和是 $\text{[math]}$ 是必然事件 B . 调查某批次汽车的抗撞击能力，适宜全面调查 C . 一组数据2，4，6，x ， 7，4，6，9的众数是4，则这组数据的中位数是4 D . 在一次芭蕾舞比赛中，甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》，两团女演员的身高平均数相同，方差分别为 $\text{[math]}$ ， $\text{[math]}$ ，则甲芭蕾舞团的女演员身高更整齐

答案解析收藏纠错 + 选题
2. (2024·山西) 一个不透明的盒子里装有一个红球、一个白球和一个绿球，这些球除颜色外都相同．从中随机摸出一个球，记下颜色后不放回，再从中随机摸出一个球，则两次摸到的球恰好有一个红球的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024·绵竹模拟) “四大古典名著”是中国文学史中的经典作品，是宝贵的世界文化遗产．小沈同学收集到中国古代四大名著卡片，四张卡片除内容外其余完全相同，将这四张卡片背面朝上，洗匀后，从中随机抽取一张（不放回），再从中随机抽取另一张，则抽到的两张卡片恰好是“水浒传”和“西游记”的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024·连云港) 下列说法正确的是（）

A . 10张票中有1张奖票，10人去摸，先摸的人摸到奖票的概率较大 B . 从1，2，3，4，5中随机抽取一个数，取得偶数的可能性较大 C . 小强一次掷出3颗质地均匀的骰子，3颗全是6点朝上是随机事件 D . 抛一枚质地均匀的硬币，正面朝上的概率为 $\text{[math]}$ ，连续抛此硬币2次必有1次正面朝上

答案解析收藏纠错 + 选题
5. (2024·广州模拟) 如图， $\text{[math]}$ 是一个等腰直角三角形纸板， $\text{[math]}$ ，在此三角形内部作一个正方形DEFG ，使DE在AC边上，点F ， G分别在BC ， AB边上.将一个飞镖随机投掷到这个纸板上，则飞镖落在阴影区域的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2018九上·武汉期末) 抛掷一枚质地均匀的硬币，正面朝上的概率为0.5，下列说法正确的是（）

A . 连续抛掷2次必有1次正面朝上 B . 连续抛掷10次不可能都正面朝上 C . 大量反复抛掷每100次出现正面朝上50次 D . 通过抛掷硬币确定谁先发球的比赛规则是公平的

答案解析收藏纠错 + 选题
7. (2024·峰峰矿模拟) 【背景材料】人的眼皮有单眼皮与双眼皮，这是由对应的基因决定的．研究表明：决定眼皮单双的基因有两种，一种是显性基因（记为B），另一种是隐性基因（记为b）；一个人的基因总是成对出现（如 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ），在成对的基因中，一个来自父亲，另一个来自母亲，父母亲提供基因时均为随机的．只要出现了显性基因B，那么这个人就一定是双眼皮。即基因 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 均为双眼皮．
【知识应用】现有一对夫妻，两人成对的基因都是 $\text{[math]}$ ，若不考虑其他因素，则他们的孩子是单眼皮的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024·荆州模拟) 校篮球队员小亮训练定点投篮以提高命中率．下表是小亮一次训练时的进球情况：
投篮数（次）
50
100
150
200
…·
进球数（次）
40
81
118
160
…
则下列说法正确的是（）

A . 小亮每投10个球，一定有8个球进 B . 小亮投球前8个进，第9，10个一定不进 C . 小亮比赛中的投球命中率一定为80% D . 小亮比赛中投球命中率可能超过80%

答案解析收藏纠错 + 选题
9. (2024·贵州模拟) 在一个黑色盒子里有1个白球，现在放入若干个黑球，它们与白球除了颜色外都相同，搅匀后从中任意摸出两个球，使得 $\text{[math]}$ （摸出一白一黑） $\text{[math]}$ （摸出两黑），则放入的黑球个数为（）

A . 3 B . 4 C . 5 D . 6

答案解析收藏纠错 + 选题
10. (2015九上·新泰竞赛) 准备两张大小一样，分别画有不同图案的正方形纸片，把每张纸都对折、剪开，将四张纸片放在盒子里，然后混合，随意抽出两张正好能拼成原图的概率是（）.

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（每题3分，共18分）

11. (2023九上·青羊月考) 有三张正面分别标有数字 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的不透明卡片，它们除数字不同外其余全部相同 $\text{[math]}$ 现将它们背面朝上，洗匀后从中任意抽取一张，将该卡片正面上的数字记为 $\text{[math]}$ ；不放回，再从中任意抽取一张，将该卡片正面朝上的数字记为 $\text{[math]}$ ，则使关于 $\text{[math]}$ 的不等式组 $\text{[math]}$ 的解集中有且只有 $\text{[math]}$ 个非负整数的概率为．

答案解析收藏纠错 + 选题
12. (2024·苏州) 如图，正八边形转盘被分成八个面积相等的三角形，任意转动这个转盘一次，当转盘停止转动时，指针落在阴影部分的概率是．

答案解析收藏纠错 + 选题
13. (2024·成都) 盒中有 $\text{[math]}$ 枚黑棋和 $\text{[math]}$ 枚白棋，这些棋除颜色外无其他差别.从盒中随机取出一枚棋子，如果它是黑棋的概率是 $\text{[math]}$ ，则 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
14. (2024·南宁模拟) 如表是某种植物的种子在相同条件下发芽率试验的结果．
种子个数
100
400
900
1500
2500
4000
发芽种子个数
92
352
818
1336
2251
3601
发芽种子频率
0.92
0.88
0.91
0.89
0.90
0.90
根据表中的数据，可估计该植物的种子发芽的概率为．（精确到0.1）

答案解析收藏纠错 + 选题
15. (2024·罗湖模拟) 如图，“中国七巧板”是由七个几何图形组成的正方形，其中1、2、3、5、7是等腰直角三角形，4是正方形，6是平行四边形，一只体型微小的小虫在七巧板上随机停留，则刚好停在6号板区域的概率是．

答案解析收藏纠错 + 选题
16. (2024·威远模拟) 有五张卡片（形状、大小、质地都相同），上面分别画有下列图形：
①线段；②正三角形；③平行四边形；④等腰梯形；⑤圆．
将卡片背面朝上洗匀，从中抽取一张，正面图形一定满足既是轴对称图形，又是中心对称图形的概率是．

答案解析收藏纠错 + 选题

三、解答题（共7题，共72分）

17. (2024·扬州) $\text{[math]}$ 年“五一”假期，扬州各旅游景区持续火热．小明和小亮准备到东关街、瘦西湖、运河三湾风景区、个园、何园 $\text{[math]}$ 分别记作 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 参加公益讲解活动．
1. （1）若小明在这 $\text{[math]}$ 个景区中随机选择 $\text{[math]}$ 个景区，则选中东关街的概率是；
2. （2）小明和小亮在 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三个景区中，各自随机选择 $\text{[math]}$ 个景区，请用画树状图或列表的方法，求小明和小亮选到相同景区的概率．
答案解析收藏纠错 + 选题
18. (2024·烟台中考) “山海同行，舰回烟台”.2024年4月23日，烟台舰与家乡人民共庆人民海军成立75周年．值此，某学校开展了“奋进万亿新征程，共筑强国强军梦”的主题研学活动．为了解学生参与情况，随机抽取部分学生对研学活动时长（用t表示，单位：h）进行调查．经过整理，将数据分成四组（A组：0≤t＜2；B组：2≤t＜4；C组：4≤t＜6；D组：6≤t＜8），并绘制了如下不完整的条形统计图和扇形统计图．
1. （1）请补全条形统计图；
2. （2）扇形统计图中，a的值为，D组对应的扇形圆心角的度数为；
3. （3） D组中有男、女生各两人，现从这四人中随机抽取两人进行研学宣讲，请用树状图或表格求所抽取的两人恰好是一名男生和一名女生的概率．
答案解析收藏纠错 + 选题
19. (2024·广安) 睡眠管理作为“五项管理”中的重要内容之一，也是学校教育重点关注的内容.某校为了解学生平均每天睡眠时间，随机抽取该校部分学生进行问卷调查，并将结果进行了统计和整理，绘制成如下统计表和不完整的统计图.
学生类别
学生平均每天睡眠时间x(单位：小时)
A
$\text{[math]}$
B
$\text{[math]}$
C
$\text{[math]}$
D
$\text{[math]}$
E
$\text{[math]}$
1. （1）本次抽取调查的学生共有人，扇形统计图中表示C类学生平均每天睡眠时间的扇形的圆心角度数为.
2. （2）请补全条形统计图．
3. （3）被抽取调查的E类4名学生中有2名女生，2名男生．从这4人中随机抽取2人进行电话回访，请用画树状图或列表的方法，求恰好抽到2名男生的概率.
答案解析收藏纠错 + 选题
20. (2022·淄博) 某中学积极落实国家“双减”教育政策，决定增设“礼仪”“陶艺”“园艺”“厨艺”及“编程”等五门校本课程以提升课后服务质量，促进学生全面健康发展为优化师资配备，学校面向七年级参与课后服务的部分学生开展了“你选修哪门课程（要求必须选修一门且只能选修一门）？”的随机问卷调查，并根据调查数据绘制了如下两幅不完整的统计图：
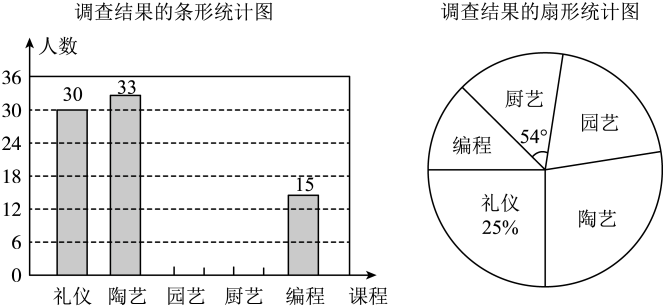
请结合上述信息，解答下列问题：
1. （1）共有名学生参与了本次问卷调查；“陶艺”在扇形统计图中所对应的圆心角是度；
2. （2）补全调查结果条形统计图；
3. （3）小刚和小强分别从“礼仪”等五门校本课程中任选一门，请用列表法或画树状图法求出两人恰好选到同一门课程的概率．
答案解析收藏纠错 + 选题
21. (2023·舒城模拟) 某县为进一步落实新课程标准理念，组织全县 $\text{[math]}$ 名教师参加新课程标准知识测试，测试后发现所有教师的成绩均不低于 $\text{[math]}$ 分．为了更好地了解本次测试的成绩分布情况，随机抽取了其中 $\text{[math]}$ 名教师的成绩（成绩x取整数，总分 $\text{[math]}$ 分）作为样本进行整理，得到下列不完整的统计图表，部分信息如下：
组名
成绩/分
频数
A
$\text{[math]}$
$\text{[math]}$
B
$\text{[math]}$
$\text{[math]}$
C
$\text{[math]}$
$\text{[math]}$
D
$\text{[math]}$
E
$\text{[math]}$
80
1. （1）这次测试成绩的中位数会落在哪一组？请补全频数分布直方图；
2. （2）若成绩在 $\text{[math]}$ 分以上（包括 $\text{[math]}$ 分）的为“优”等，则该县参加这次测试的 $\text{[math]}$ 名教师中成绩为“优”等的大约有多少人？
3. （3）已知这次测试有5名教师（3女2男）获得满分，现从中任选两人参加所在市组织的“全面育人、素养导向”大赛，求恰巧选中一名男教师和一名女教师的概率．
答案解析收藏纠错 + 选题
22. (2022·莘县模拟) 每年6月26日是“国际禁毒日”．某中学为了让学生掌握禁毒知识，提高防毒意识，组织全校学生参加了“禁毒知识网络答题”活动．该校德育处对八年级全体学生答题成绩进行统计，将成绩分为四个等级：优秀、良好、一般、不合格；并绘制成如下不完整的统计图．请你根据图1、图2中所给的信息解答下列问题：
1. （1）该校八年级共有名学生，“优秀”所占圆心角的度数为．
2. （2）请将图1中的条形统计图补充完整．
3. （3）已知该市共有15000名学生参加了这次“禁毒知识网络答题”活动，请以该校八年级学生答题成绩统计情况估计该市大约有多少名学生在这次答题中成绩不合格？
4. （4）德育处从该校八年级答题成绩前四名甲、乙、丙、丁学生中随机抽取2名同学参加全市现场禁毒知识竞赛，请用树状图或列表法求出必有甲同学参加的概率．
答案解析收藏纠错 + 选题
23. (2022·冠县模拟) 我市华恒小区居民在“一针疫苗一份心，预防接种尽责任”的号召下，积极联系社区医院进行新冠疫苗接种．为了解接种进度，该小区管理人员对小区居民进行了抽样调查，按接种情况可分如下四类：A类——接种了只需要注射一针的疫苗：B类——接种了需要注射二针，且二针之间要间隔一定时间的疫苗；C类——接种了要注射三针，且每二针之间要间隔一定时间的疫苗；D类——还没有接种，图1与图2是根据此次调查得到的统计图（不完整）．

请根据统计图回答下列问题．
1. （1）此次抽样调查的人数是多少人？
2. （2）接种B类疫苗的人数的百分比是多少？接种C类疫苗的人数是多少人？
3. （3）请估计该小区所居住的18000名居民中有多少人进行了新冠疫苗接种．
4. （4）为了继续宣传新冠疫苗接种的重要性，小区管理部门准备在已经接种疫苗的居民中征集2名志愿宣传者，现有3男2女共5名居民报名，要从这5人中随机挑选2人，求恰好抽到一男和一女的概率是多少．
答案解析收藏纠错 + 选题