全国历年中考数学真题精选汇编：四边形1

更新时间：2021-07-08 浏览次数：121 类型：二轮复习

一、单选题

1. (2024九下·徐州模拟) 若正多边形的一个内角是150°，则该正多边形的边数是（）

A . 6 B . 12 C . 16 D . 18

答案解析收藏纠错 + 选题
2. (2021八下·薛城期末) 如图，将 $\text{[math]}$ 绕边 $\text{[math]}$ 的中点O顺时针旋转180°．嘉淇发现，旋转后的 $\text{[math]}$ 与 $\text{[math]}$ 构成平行四边形，并推理如下：
点A，C分别转到了点C，A处，

而点B转到了点D处．

∵ $\text{[math]}$ ，

∴四边形 $\text{[math]}$ 是平行四边形．

小明为保证嘉淇的推理更严谨，想在方框中“∵ $\text{[math]}$ ，”和“∴四边形……”之间作补充．下列正确的是（）

A . 嘉淇推理严谨，不必补充 B . 应补充：且 $\text{[math]}$ ， C . 应补充：且 $\text{[math]}$ D . 应补充：且 $\text{[math]}$ ，

答案解析收藏纠错 + 选题
3. (2017·河北) 求证：菱形的两条对角线互相垂直．
已知：如图，四边形ABCD是菱形，对角线AC，BD交于点O．
求证：AC⊥BD．
以下是排乱的证明过程：
①又BO=DO；
②∴AO⊥BD，即AC⊥BD；
③∵四边形ABCD是菱形；
④∴AB=AD．
证明步骤正确的顺序是（）

A . ③→②→①→④ B . ③→④→①→② C . ①→②→④→③ D . ①→④→③→②

答案解析收藏纠错 + 选题
4. (2021九上·永州月考) 如图，矩形 $\text{[math]}$ 的对角线 $\text{[math]}$ 、 $\text{[math]}$ 相交于点 $\text{[math]}$ ， $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 交于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024八下·蒸湘期末) 下列说法中不正确的是（）

A . 四边相等的四边形是菱形 B . 对角线垂直的平行四边形是菱形 C . 菱形的对角线互相垂直且相等 D . 菱形的邻边相等

答案解析收藏纠错 + 选题
6. (2022八下·普兰店期中) 下列选项中，不能判定四边形ABCD是平行四边形的是 $\text{[math]}$ 　　 $\text{[math]}$

A . $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
7. 在平行四边形ABCD中，∠A的平分线把BC边分成长度是3和4的两部分，则平行四边形ABCD周长是（）

A . 22 B . 20 C . 22或20 D . 18

答案解析收藏纠错 + 选题
8. (2024九下·南山模拟) 下列命题中，假命题是( )

A . 矩形的对角线相等 B . 矩形对角线交点到四个顶点的距离相等 C . 矩形的对角线互相平分 D . 矩形对角线交点到四条边的距离相等

答案解析收藏纠错 + 选题
9. (2021八下·江阴期末) 已知平行四边形ABCD，AC、BD是它的两条对角线，那么下列条件中，能判断这个平行四边形为矩形的是（）

A . ∠BAC=∠DCA B . ∠BAC=∠DAC C . ∠BAC=∠ABD D . ∠BAC=∠ADB

答案解析收藏纠错 + 选题
10. (2016·上海) 已知在△ABC中，AB=AC，AD是角平分线，点D在边BC上，设 $\text{[math]}$ = $\text{[math]}$ ， $\text{[math]}$ = $\text{[math]}$ ，那么向量 $\text{[math]}$ 用向量 $\text{[math]}$ 、 $\text{[math]}$ 表示为（）

A . $\text{[math]}$ $\text{[math]}$ + $\text{[math]}$ B . $\text{[math]}$ $\text{[math]}$ ﹣ $\text{[math]}$ C . ﹣ $\text{[math]}$ $\text{[math]}$ + $\text{[math]}$ D . ﹣ $\text{[math]}$ $\text{[math]}$ ﹣ $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2023九上·大田期中) 下列结论中，矩形具有而菱形不一定具有的性质是（）

A . 内角和为360° B . 对角线互相平分 C . 对角线相等 D . 对角线互相垂直

答案解析收藏纠错 + 选题
12. (2020·东城模拟) 如图，三角板的直角顶点落在矩形纸片的一边上，若∠1＝35°，则∠2的度数是（）。

A . 35° B . 45° C . 55° D . 65°

答案解析收藏纠错 + 选题
13. (2022八下·双城期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点D，E，F分别是AB，BC，CA的中点，连结DE，EF，则四边形ADEF的周长为（）

A . 6 B . 9 C . 12 D . 15

答案解析收藏纠错 + 选题
14. (2023八下·景县期末) 下是关于某个四边形的三个结论：①它的对角线相等；②它是一个正方形；③它是一个矩形.下列推理过程正确的是（）

A . 由②推出③，由③推出① B . 由①推出②，由②推出③ C . 由③推出①，由①推出② D . 由①推出③，由③推出②

答案解析收藏纠错 + 选题
15. (2022·绍兴模拟) 四边形具有不稳定性，对于四条边长确定的四边形，当内角度数发生变化时，其形状也会随之改变，如图，改变正方形ABCD的内角，正方形ABCD变为菱形ABC′D′，若∠D′AB＝30°，则菱形ABC′D′的面积与正方形ABCD的面积之比是（）

A . 1 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
16. (2018·宁波) 如图，在▱ABCD中，对角线AC与BD相交于点O，E是边CD的中点，连结OE．若∠ABC=60°，∠BAC=80°，则∠1的度数为（）

A . 50° B . 40° C . 30° D . 20°

答案解析收藏纠错 + 选题
17. (2023八上·市北区月考) 我国古代伟大的数学家刘徽将勾股形（古人称直角三角形为勾股形）分割成一个正方形和两对全等的直角三角形，得到一个恒等式．后人借助这种分割方法所得的图形证明了勾股定理，如图所示的矩形由两个这样的图形拼成，若 $\text{[math]}$ ， $\text{[math]}$ ，则该矩形的面积为（）

A . 20 B . 24 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

18. (2024八下·北京市期中) 在矩形ABCD中，M，N，P，Q分别为边AB，BC，CD，DA上的点（不与端点重合）．对于任意矩形ABCD，下面四个结论中，①存在无数个四边形MNPQ是平行四边形；②存在无数个四边形MNPQ是矩形；③存在无数个四边形MNPQ是菱形；④至少存在一个四边形MNPQ是正方形．所有正确结论的序号是．

答案解析收藏纠错 + 选题
19. (2017·河北) 如图，A，B两点被池塘隔开，不能直接测量其距离．于是，小明在岸边选一点C，连接CA，CB，分别延长到点M，N，使AM=AC，BN=BC，测得MN=200m，则A，B间的距离为m．

答案解析收藏纠错 + 选题
20. (2017·山西) 一副三角板按如图方式摆放，得到△ABD和△BCD，其中∠ADB=∠BCD=90°，∠A=60°，∠CBD=45°，E为AB的中点，过点E作EF⊥CD于点F．若AD=4cm，则EF的长为 cm．

答案解析收藏纠错 + 选题
21. (2020九上·临泽期中) 如图，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ．若将 $\text{[math]}$ 沿 $\text{[math]}$ 折叠，点 $\text{[math]}$ 与边 $\text{[math]}$ 的中点 $\text{[math]}$ 恰好重合，则四边形 $\text{[math]}$ 的周长为．

答案解析收藏纠错 + 选题
22. (2021八下·滨城期末) 如图，在四边形ABCD中，AD//BC，在不添加任何辅助线的情况下，请你添加一个条件，使四边形ABCD是平行四边形（填一个即可）．

答案解析收藏纠错 + 选题
23. (2020·牡丹江) 如图，在四边形 $\text{[math]}$ 中，连接 $\text{[math]}$ ， $\text{[math]}$ ．请你添加一个条件，使 $\text{[math]}$ ．（填一种情况即可）

答案解析收藏纠错 + 选题
24. (2020·上海) 如图，AC、BD是平行四边形ABCD的对角线，设 $\text{[math]}$ = $\text{[math]}$ ， $\text{[math]}$ = $\text{[math]}$ ，那么向量 $\text{[math]}$ 用向量 $\text{[math]}$ 表示为．

答案解析收藏纠错 + 选题
25. (2024·兴化模拟) 通过画出多边形的对角线，可以把多边形内角和问题转化为三角形内角和问题．如果从某个多边形的一个顶点出发的对角线共有2条，那么该多边形的内角和是度．

答案解析收藏纠错 + 选题
26. (2023·长沙模拟) 如图，四边形 $\text{[math]}$ 为菱形， $\text{[math]}$ ，延长 $\text{[math]}$ 到 $\text{[math]}$ ，在 $\text{[math]}$ 内作射线 $\text{[math]}$ ，使得 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ ，垂足为 $\text{[math]}$ ，若 $\text{[math]}$ ，则对角线 $\text{[math]}$ 的长为.（结果保留根号）

答案解析收藏纠错 + 选题
27. (2020·徐州) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 分别为 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的中点，若 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
28. (2019九上·海淀月考) 如图，已知点E在正方形ABCD的边AB上，以BE为边向正方形ABCD外部作正方形BEFG，连接DF，M、N分别是DC、DF的中点，连接MN.若AB=7，BE=5，则MN=.

答案解析收藏纠错 + 选题
29. 如图， $\text{[math]}$ ABCD的对角线AC，BD相交于点O，请添加一个条件：，使 $\text{[math]}$ ABCD是菱形。

答案解析收藏纠错 + 选题
30. 如图，平移图形M，与图形N可以拼成一个平行四边形，则图中α的度数是°.

答案解析收藏纠错 + 选题

三、解答题

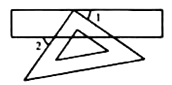
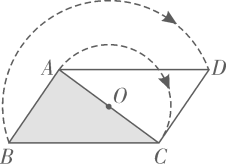
31. (2017·北京) 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线，则所容两长方形面积相等（如图所示）”这一推论，他从这一推论出发，利用“出入相补”原理复原了《海岛算经》九题古证．
（以上材料来源于《古证复原的原理》、《吴文俊与中国数学》和《古代世界数学泰斗刘徽》）

请根据该图完成这个推论的证明过程．

证明：S_矩形NFGD=S_△ADC﹣（S_△ANF+S_△FGC），S_矩形EBMF=S_△ABC﹣（+）．

易知，S_△ADC=S_△ABC ， =，=．

可得S_矩形NFGD=S_矩形EBMF ．

答案解析收藏纠错 + 选题

四、综合题

32. (2022八上·莱西期末) 如图，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，对角线 $\text{[math]}$ ， $\text{[math]}$ 交于点 $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）求证：四边形 $\text{[math]}$ 是菱形；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
33. (2022八下·江北期中) 如图，在四边形ABCD中，BD为一条对角线，AD∥BC，AD=2BC，∠ABD=90°，E为AD的中点，连接BE．
1. （1）求证：四边形BCDE为菱形；
2. （2）连接AC，若AC平分∠BAD，BC=1，求AC的长．
答案解析收藏纠错 + 选题
34. (2021七下·洪洞期末) 已知n边形的内角和θ=（n-2）×180°.
1. （1）甲同学说，θ能取360°；而乙同学说，θ也能取630°.甲、乙的说法对吗？若对，求出边数n.若不对，说明理由；
2. （2）若n边形变为（n+x）边形，发现内角和增加了360°，用列方程的方法确定x.
答案解析收藏纠错 + 选题
35. (2019·吉林) 图①，图②均为 $\text{[math]}$ 的正方形网格，每个小正方形的顶点称为格点．在图①中已画出线段 $\text{[math]}$ ，在图②中已画出线段 $\text{[math]}$ ，其中 $\text{[math]}$ 均为格点，按下列要求画图：
1. （1）在图①中，以 $\text{[math]}$ 为对角线画一个菱形 $\text{[math]}$ ，且 $\text{[math]}$ 为格点；
2. （2）在图②中，以 $\text{[math]}$ 为对角线画一个对边不相等的四边形 $\text{[math]}$ ，且 $\text{[math]}$ 为格点， $\text{[math]}$ .
答案解析收藏纠错 + 选题
36. (2018·吉林) 如图①，在△ABC中，AB=AC，过AB上一点D作DE∥AC交BC于点E，以E为顶点，ED为一边，作∠DEF=∠A，另一边EF交AC于点F．
1. （1）求证：四边形ADEF为平行四边形；
2. （2）当点D为AB中点时，▱ADEF的形状为；
3. （3）延长图①中的DE到点G，使EG=DE，连接AE，AG，FG，得到图②，若AD=AG，判断四边形AEGF的形状，并说明理由．
答案解析收藏纠错 + 选题
37. (2023八下·浏阳期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 的角平分线交 $\text{[math]}$ 于点D， $\text{[math]}$ .
1. （1）试判断四边形 $\text{[math]}$ 的形状，并说明理由；
2. （2）若 $\text{[math]}$ ，且 $\text{[math]}$ ，求四边形 $\text{[math]}$ 的面积.
答案解析收藏纠错 + 选题
38. (2023九上·云南开学考) 如图，点C是 $\text{[math]}$ 的中点，四边形 $\text{[math]}$ 是平行四边形.
1. （1）求证：四边形 $\text{[math]}$ 是平行四边形；
2. （2）如果 $\text{[math]}$ ，求证：四边形 $\text{[math]}$ 是矩形.
答案解析收藏纠错 + 选题
39. (2019·湖州) 如图，已知在△ABC中，D，E，F分别是AB，BC，AC的中点，连结DF，EF，BF.
1. （1）求证：四边形BEFD是平行四边形；
2. （2）若∠AFB＝90°，AB＝6，求四边形BEFD的周长.
答案解析收藏纠错 + 选题
40. (2019·杭州) 如图，已知正方形ABCD的边长为1，正方形CEFG的面积为S₁ ，点E在DC边上，点G在BC的延长线上，设以线段AD和DE为邻边的矩形的面积为 S₂ ，且S₁=S₂.
1. （1）求线段CE的长.
2. （2）若点日为BC边的中点，连接HD，求证：HD=HG.
答案解析收藏纠错 + 选题