 B .
B .  C .
C .  D .
D . 
⑴有两个角互余的三角形是直角三角形;(2)有一个角等于60°的等腰三角形是等边三角形;(3)等腰三角形的角平分线、中线、高互相重合;(4)在角的内部,到角的两边距离相等的点在这个角的平分线上.
①圆柱由3个面围成,这3个面都是平的;②圆锥由2个面围成,这2个面中,1个是平的,1个是曲的;③球仅由1个面围成,这个面是平的;④正方体由6个面围成,这6个面都是平的.其中正确的为( )
①若 ,则
只能是
;②若
的运算结果中不含
项,则
③若
,
,则
④若
,
,则
可表示为

①当△ABC满足条件AB=AC时,四边形AFBD是形;
② 当△ABC满足条件时,四边形AFBD是正方形.

解:∵∠BDC=∠A+∠ACD( ▲ ),
∴∠BDC=62°+35°=97°(等量代换).
∵∠BFD+∠BDC+∠ABE= ▲ ( ▲ ),
∴∠BFD=180°﹣∠BDC﹣∠ABE=180°﹣97°﹣20°=63°(等式的性质).
已知:如图, 和
中,
,
,
求证:

证明:
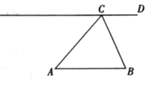
求作:线段BP,使得点P在直线CD上,且∠ABP= .
作法:①以点A为圆心,AC长为半径画圆,交直线CD于C,P两点;②连接BP.线段BP就是所求作线段.
证明:∵CD∥AB,
∴∠ABP=.
∵AB=AC,
∴点B在⊙A上.
又∵∠BPC= ∠BAC()(填推理依据)
∴∠ABP= ∠BAC

①图1中∠ABC与∠DEF数量关系为;图2中∠ABC与∠DEF数量关系为;
请选择其中一种情况说明理由.
②由①得出一个真命题(用文字叙述):.
若两个角的两边互相平行,且一个角比另一个角的2倍少30°,请直接写出这两个角的度数.

推理过程:
因为: ,
( )
所以:
也就有 ( )
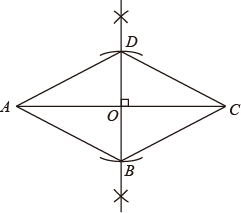
|
已知:如图,在四边形ABCD中, BC=AD, AB=____________, 求证:四边形ABCD是_________________四边形。 |

证明:
|
婆罗摩笈多(Brahmagupta)是古印度著名数学家、天文学家,他在三角形、四边形、零和负数的算术运算规则、二次方程等方面均有建树,特别是在研究一阶和二阶不定方程方面作出了巨大贡献.他曾经提出了“婆罗摩笈多定理”,该定理也称为“古拉美古塔定理”.该定理的内容及部分证明过程如下: 古拉美古塔定理:已知:如图,四边形ABCD内接于⊙O,对角线AC⊥BD,垂足为M,直线ME⊥BC,垂足为E,并且交直线AD于点F,则AF=FD. 证明:∵AC⊥BD,ME⊥BC ∴∠CME+∠C=90°,∠CBD+∠C=90° ∴∠CBD=∠CME ∴ ,∠CME=∠AMF ∴∠CAD=∠AMF ∴AF=MF … |
任务:
已知:如图,四边形ABCD内接于⊙O,对角线AC⊥BD,垂足为M,F为AD上一点,直线FM交BC于点E,

① ▲ .
求证:② ▲ .
证明:
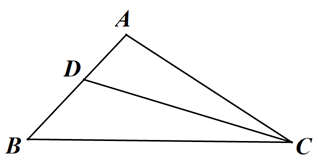
求作:菱形DFCE , 使点F在BC边上,点E在AC边上,下面是尺规作图过程.
作法:①分别以C、D为圆心,大于 为半径作弧,两弧分别交于点M、N;
②作直线MN分别与AC、BC交于点E、F;
③连接DE、DF , DC与EF的交点记为点G;四边形DFCE为所求作的菱形.
证明: ,
为DC的垂直平分线.
,
.
平分
,
.
,
▲
▲ ( )(填推理依据)
同理可证 ,
四边形DFCE为平行四边形.
又 ▲ ,
四边形DFCE为菱形.




