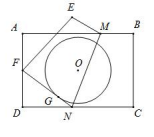

⑴H是FK的中点
⑵△HGD≌△HEC
⑶S△AHG:S△DHC=9:16
⑷DK=
⑸HG⊥HC




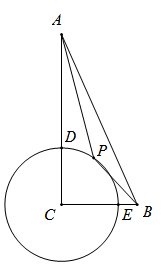

①PB=PD;② 的长为
π;③∠DBE=45°;④△BCF∽△PFB;⑤CF•CP为定值.



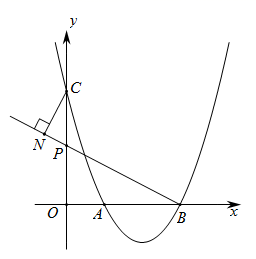
①设与
的周长分别为
和
, 试判断
的值是否发生变化,若不变则求出该值;若变化请说明理由;
②若 , 求
的长.

①求∠CDE的取值范围;
②如图2,取DE的中点G,连接CG并延长交直线DF于点H,点P为正方形内一动点,试求PH+PA+PB的最小值.

①当点O在QD上时,求t的值;
②当PQ与⊙O有公共点时,求t的取值范围.

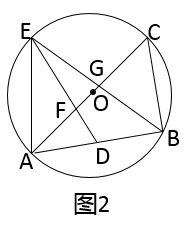
①求证: 是智慧三角形;
②设 ,若⊙O的半径为
,求
关于
的函数表达式;


①用含t的代数式表示DE2.
②记S=DE•EG,求S关于t的函数表达式.
