



①求证:四边形AFCE为平行四边形;
②若CA平分∠BCD , ∠AEC=60°,求四边形AFCE的周长.



①当 与
满足什么数量关系时,四边形
是矩形?请说明理由;
②若 ,
,
,求四边形
的面积.
“勤奋小组”的同学把这两张纸片按如图2的方式摆放,点A与点D重合,连接 和
. 他们发现
和
之间存在着一定的数量关系,这个关系是.
“创新小组”的同学在“勤奋小组”的启发下,把这两张纸片按如图3的方式摆放,点F,A,D,C在同一直线上,连接 和
, 他们发现了
和
之间的数量和位置关系,请写出这些关系并说明理由;
请你利用 和
纸片进行拼摆,将拼摆出的图形画在图4中(要求不得与图2,图3相同),并根据图形写出一条正确的数学结论.
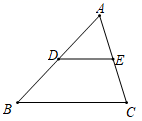
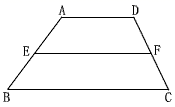
①如图,在四边形ABCD中,AD∥BC,E、F分别是AB、CD的中点,求证:EF∥BC,FE= (AD+BC)
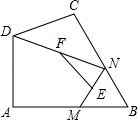
②如图,在四边形ABCD中,∠A=90°,AB=3 ,AD=3,点M,N分别在边AB,BC上,点E,F分别为MN,DN的中点,连接EF,求EF长度的最大值.
①如图,若 ,
,
,则
( );
②如图,试探索 、
、
之间的数量关系,并将你的探索过程写下来.