2022年江苏省扬州市中考数学模拟卷1

更新时间：2022-04-27 浏览次数：128 类型：中考模拟

一、选择题（每题3分，共24分）

1. (2022九下·杭州月考) ﹣2022的倒数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . ﹣2022 D . 2022

答案解析收藏纠错 + 选题
2. (2022·高安模拟) 如图，是一个小正方体的展开图，把展开图折叠成小正方体后，有“三”字一面的相对面上的字是（）

A . 高 B . 同 C . 创 D . 安

答案解析收藏纠错 + 选题
3. (2022九上·无为月考) 下列事件中，属于必然事件的是（）

A . 打开电视正在播广告 B . 射击运动员只射击1次，恰好命中靶心 C . 一组数据的方差越小，则这组数据的波动越小 D . 任意购买一张电影票，座位号是3的倍数

答案解析收藏纠错 + 选题
4. (2020八上·龙口期末) 若分式 $\text{[math]}$ 的值为0，则x的值为（）

A . 2 B . -2 C . ±2 D . 4

答案解析收藏纠错 + 选题
5. (2022·高安模拟) 如图， $\text{[math]}$ 与 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别交于点E，G，F，且 $\text{[math]}$ ， $\text{[math]}$ ，则下列结论不正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021九上·无锡期中) 如图，△ABC中，AB=AC= $\text{[math]}$ ，∠BAC=α°， $\text{[math]}$ ，G为BC中点，D为平面内一个动点，且 $\text{[math]}$ .将线段BD绕点D逆时针旋转α°，得到DB′，则四边形BACB′面积的最大值为（）

A . 24 B . 25 C . 12 D . 13

答案解析收藏纠错 + 选题
7. (2022·齐齐哈尔模拟) 如图，正方形ABCD的边长为4，E是BC上一点，过点E作EF⊥AE，交DC于点F，连接AF，则AF的最小值是（）

A . 5 B . $\text{[math]}$ C . $\text{[math]}$ D . 3

答案解析收藏纠错 + 选题
8. (2022·交城模拟) 如图，正方形ABCD的边长是 $\text{[math]}$ ，以正方形对角线的一半OA为边作正六边形，其中一边与正方形的边CD交于点E，再以点O为圆心OE为半径画弧交AD于点F，则图中阴影部分的的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（每题3分，共30分）

9. (2022·齐齐哈尔模拟) 某网店2022年母亲节这天的营业额为221000元，将数221000用科学记数法表示为．

答案解析收藏纠错 + 选题
10. (2024九下·仪征模拟) 若 $\text{[math]}$ 、 $\text{[math]}$ 满足 $\text{[math]}$ ，则代数式 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
11. (2022·交城模拟) 不等式组 $\text{[math]}$ 的解集是．

答案解析收藏纠错 + 选题
12. (2023八下·襄城期末) 一组数据23，27，20，18，x，12，它们的中位数是21，则x=.

答案解析收藏纠错 + 选题
13. (2023七上·南明期中) 扬州雕版印刷技艺历史悠久，元代数学家朱世杰的《算学启蒙》一书曾刻于扬州，该书是中国较早的数学著作之一，书中记载一道问题：“今有良马日行二百四十里，驽马日行一百五十里，驽马先行一十二日，问良马几何日追及之？”题意是：快马每天走240里，慢马每天走150里，慢马先走12天，试问快马几天追上慢马？答：快马天追上慢马.

答案解析收藏纠错 + 选题
14. (2021九上·东营月考) 一个“粮仓”的三视图如图所示（单位：m），则它的侧面积是．

答案解析收藏纠错 + 选题
15. (2022·齐齐哈尔模拟) 在等边△ABC中，点D在BC边上，BD＝3CD，连接AD，以AD为边作等边△ADE，连接CE，若CE＝3，则AB的长为．

答案解析收藏纠错 + 选题
16. (2022九下·定远期中) 如图，AB是半圆O的直径，AC=AD，∠CAB=20°，OE⊥CD，OE= $\text{[math]}$ ，则半圆O的直径AB是

答案解析收藏纠错 + 选题
17. (2022·河北模拟) 如图，在平面直角坐标系中，点 $\text{[math]}$ ，点 $\text{[math]}$ ， I是 $\text{[math]}$ 的内心，则
1. （1） AB=；
2. （2）点I关于x轴对称的点的坐标是．
答案解析收藏纠错 + 选题
18. (2022·合肥模拟) 如图①，我们把一个矩形称作一个基本图形，把矩形的顶点及其对称中心称作基本图形的特征点，显然这样的基本图形共有5个特征点，将此基本图形不断地复制并平移，使得相邻两个基本图形的两个特征点重合，这样得到第2个图；第3个图；……；
1. （1）观察以上图形并完成下表：
  基本图形的个数
  1
  2
  3
  4
  …
  特征点的个数
  5
  8
  11
  …
  猜想：在第n个图中特征点的个数为（用含n的代数式表示）．
2. （2）在平面直角坐标系中，点A、点B是坐标轴上的两点，且OA＝1，以OA、OB为边作一个矩形，其一条对角线所在直线的解析式为y＝ $\text{[math]}$ x，将此矩形作为基本图形不断复制和平移，如图②所示，若各矩形的对称中心分别为O₁、O₂、O₃、……，则O₂₀₂₂的坐标为．
答案解析收藏纠错 + 选题

三、解答题（共10题，共96分）

19. (2022九下·江津期中)
1. （1）（a+b）（a-2b）-（a-b）²-b（a-b）．
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
20. (2024九下·海门月考) “通过等价变换，化陌生为熟悉，化未知为已知”是数学学习中解决问题的基本思维方式，例如：解方程 $\text{[math]}$ ，就可以利用该思维方式，设 $\text{[math]}$ ，将原方程转化为： $\text{[math]}$ 这个熟悉的关于y的一元二次方程，解出y，再求x，这种方法又叫“换元法”．请你用这种思维方式和换元法解决下面的问题．已知实数x，y满足 $\text{[math]}$ ，求 $\text{[math]}$ 的值．

答案解析收藏纠错 + 选题
21. (2022·瑞金模拟) 家庭过期药品属于“国家危险废物”，处理不当将污染环境，危害健康．某校学生杨杨和舟舟为了解市民家庭处理过期药品的方式，决定对全市家庭作一次简单随机抽样调查．
1. （1）下列选取样本的方法最合理的一种是．（只需填上符合题意答案的序号）
  ①在市中心某个居民区以家庭为单位随机抽取；
  ②在全市医务工作者中以家庭为单位随机抽取；
  ③在全市常住人口中以家庭为单位随机抽取．
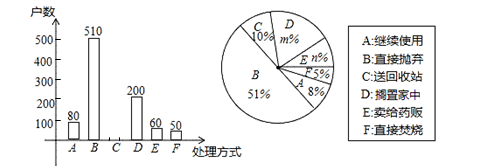
2. （2）本次抽样调查发现，接受调查的家庭都有过期药品，现将有关数据呈现如图：
  ①m= ▲ ；n= ▲ ；
  ②补全条形统计图；
  ③根据调查数据，你认为该市市民家庭处理过期药品最常见的方式是 ▲ ；
  ④家庭过期药品的正确处理方式是送回收站点，若该市有180万户家庭，请估计大约有多少户家庭处理过期药品的方式是送回收站点．
答案解析收藏纠错 + 选题
22. (2024·惠城模拟) 如图，线段AD是△ABC的角平分线.
1. （1）尺规作图：作线段AD的垂直平分线分别交AB，AC于点E，F：（保留痕迹，不写作法）
2. （2）在（1）所作的图中，连接DE，DF，求证：四边形AEDF是菱形.
答案解析收藏纠错 + 选题
23. (2022·新余模拟) 为庆祝“三八妇女节”，某地举行歌咏比赛，歌曲有：《我爱你，中国》，《歌唱祖国》，《我和我的祖国》（分别用字母A，B，C依次表示这三首歌曲）．比赛时，将A，B，C这三个字母分别写在3张无差别不透明的卡片正面上，洗匀后正面向下放在桌面上，甲先从中随机抽取一张卡片，放回后洗匀，再由乙从中随机抽取一张卡片，进行歌咏比赛．
1. （1）甲抽中歌曲《我和我的祖国》的概率是；
2. （2）试用画树状图或列表的方法表示所有可能的结果，并求出甲和乙抽中不同歌曲的概率．
答案解析收藏纠错 + 选题
24. (2022·净月模拟) 为保障新冠病毒疫苗接种需求，某生物科技公司开启“加速”模式，生产效率比原先提高了20%，现在生产240万剂疫苗所用的时间比原先生产220万剂疫苗所用的时间少0.5天，问原先每天生产多少万剂疫苗？

答案解析收藏纠错 + 选题
25. (2023·婺城模拟) 如图，点A，C是 $\text{[math]}$ 上的点，且 $\text{[math]}$ ，过点A作 $\text{[math]}$ ，连接BC交 $\text{[math]}$ 于点D，点D是BC的中点．
1. （1）求 $\text{[math]}$ 的度数；
2. （2）求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
26. (2022·云南模拟) 已知抛物线y＝ax²＋bx＋c与x轴交于A（﹣1，0），B（5，0）两点，C为抛物线的顶点，抛物线的对称轴交x轴于点D，连接BC，且tan∠CBD $\text{[math]}$ ，如图所示．
1. （1）求抛物线的解析式；
2. （2）设P是抛物线的对称轴上的一个动点．
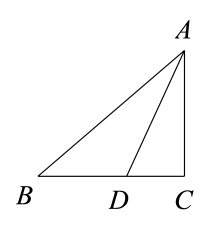
  ①过点P作x轴的平行线交线段BC于点E，过点E作EF⊥PE交抛物线于点F，连接FB、FC，求△BCF的面积的最大值；
  ②连接PB，求 $\text{[math]}$ PC＋PB的最小值．
答案解析收藏纠错 + 选题
27. (2022·齐齐哈尔模拟) 实践与探究
情境：在正方形ABCD中，AB＝5，点F在AC上，且 $\text{[math]}$ ，过点F作EF⊥AC，交CD于点E，连接AE，AF．
1. （1）问题发现
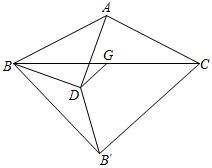
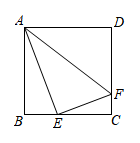
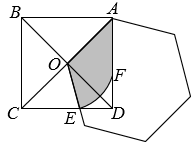
  图（1）中，线段AE与BF的数量关系是；
  直线AE与直线BF的夹角的度数是．
2. （2）问题拓展
  当△CEF绕点C顺时针旋转时，（1）中的结论是否成立？若成立，请仅就图2的情形给出证明；若不成立，说明理由．
3. （3）问题延伸
  在（2）的条件下，当点F到直线BC的距离为2时，直接写出AE的长．
答案解析收藏纠错 + 选题
28. (2022·齐齐哈尔模拟) 综合与探究
如图，抛物线 $\text{[math]}$ 与x轴交于点A（－1，0），点B（3，0），与y轴交于点C，对称轴与x轴交于点D，点P是直线BC上方抛物线上一点．
1. （1）求抛物线的解析式；
2. （2）在直线BC上方的抛物线上找一点P，作PG⊥BC，当PG为最大值时，求线段PD的长；
3. （3）连接CD、CB，当∠PCB＝∠DCB时，求点P的坐标．
4. （4）若点M为直线BC上一点，N为平面内一点，是否存在这样的点M和点N使得以C、D、M、N为顶点的四边形是菱形？若存在，直接写出点M坐标；若不存在，说明理由．
答案解析收藏纠错 + 选题