2022年南京市中考数学超级风向标押题卷一

更新时间：2022-05-26 浏览次数：202 类型：中考模拟

一、单选题（每题2分，共12分）

1. (2022·高要模拟) 下列运算中，正确的是（）．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022九下·江津期中) 下列实数，介于5和6之间的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2022·武安模拟) 如图，将数轴上－4与8两点间的线段六等分，五个等分点所对应的数依次为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则下列结论不正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022·海淀模拟) 某校举办校庆晚会，其主舞台为一圆形舞台，圆心为O．A，B是舞台边缘上两个固定位置，由线段AB及优弧 $\text{[math]}$ 围成的区域是表演区．若在A处安装一台某种型号的灯光装置，其照亮区域如图1中阴影所示．若在B处再安装一台同种型号的灯光装置，恰好可以照亮整个表演区，如图2中阴影所示．
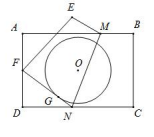
若将灯光装置改放在如图3所示的点M，N或P处，能使表演区完全照亮的方案可能是（）
①在M处放置2台该型号的灯光装置
②在M，N处各放置1台该型号的灯光装置
③在P处放置2台该型号的灯光装置

A . ①② B . ①③ C . ②③ D . ①②③

答案解析收藏纠错 + 选题
5. (2022·青浦模拟) 如图，在平面直角坐标系中，已知 $\text{[math]}$ ， $\text{[math]}$ ，以 $\text{[math]}$ 为顶点， $\text{[math]}$ 为一边作 $\text{[math]}$ 角，角的另一边交 $\text{[math]}$ 轴于C（C在B上方），则C坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022九下·蓬安开学考) 矩形ABCD中，AB＝12，BC＝8，将矩形沿MN折叠，使点C恰好落在AD边的中点F处，以矩形对称中心O点为圆心的圆与FN相切于点G，则⊙O的半径为（）

A . 3.6 B . $\text{[math]}$ C . 3.5 D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（每题2分，共20分）

7. (2022·红河模拟) 若二次根式 $\text{[math]}$ 有意义，则x的取值范围为．

答案解析收藏纠错 + 选题
8. (2022·贵港模拟) 2022年北京冬奥会圆满成功，北京成为迄今为止唯一一个既举办过夏季奥运会，又举办过冬季奥运会的城市，据统计北京冬奥会开幕式中国大陆地区观看人数约3.16亿人，其中3.16亿用科学记数法表示为.

答案解析收藏纠错 + 选题
9. (2021·海东模拟) 分解因式： $\text{[math]}$ ；分式方程： $\text{[math]}$ 解为．

答案解析收藏纠错 + 选题
10. (2022·肇源模拟) 一元二次方程 $\text{[math]}$ 的两根为 $\text{[math]}$ 、 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
11. (2022·青岛模拟) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
12. (2022·青浦模拟) 如图，是实验室里一批种子的发芽天数统计图，其中“1天发芽”的圆心角和“3天发芽”的百分比如图所示，“2天发芽”与“4天发芽”的扇形弧长相等．则这批种子的平均发芽天数为．

答案解析收藏纠错 + 选题
13. (2022九下·虹口期中) 已知 $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 之间的距离是5cm，圆心O到直线 $\text{[math]}$ 的距离是2cm，如果圆O与直线 $\text{[math]}$ 、 $\text{[math]}$ 有三个公共点，那么圆O的半径为cm．

答案解析收藏纠错 + 选题
14. (2022·龙华模拟) 如图，点 A 是反比例函数 $\text{[math]}$ （k≠0，x<0）图象上的一点，经过点 A 的直线与坐标轴分别交于点C和点D，过点A作AB⊥y轴于点B， $\text{[math]}$ ，连接BC，若△BCD的面积为2，则k的值为．

答案解析收藏纠错 + 选题
15. (2022·道外模拟) 在△ABC中，点D为AC边的中点， $\text{[math]}$ 于点E，△DEF为等边三角形，若 $\text{[math]}$ ， $\text{[math]}$ ，则DE的长为．

答案解析收藏纠错 + 选题
16. (2022·东营模拟) 如图，抛物线 $\text{[math]}$ 与x轴交于A、B两点，P是以点 $\text{[math]}$ 为圆心，2为半径的圆上的动点，Q是线段PA的中点，连结OQ．则线段OQ的最小值是．

答案解析收藏纠错 + 选题

三、解答题（共11题，共88分）

17. (2022·顺义模拟) 解不等式组 $\text{[math]}$ ，并写出它的所有整数解．

答案解析收藏纠错 + 选题
18. (2022·福田模拟) 化简求值： $\text{[math]}$ ，其中 $\text{[math]}$ ；

答案解析收藏纠错 + 选题
19. (2022八下·无棣期中) 课堂上，同学们在讨论解答数学课本50页综合运用的第9题“如图，在梯形ABCD中，AB∥CD，已知∠A=∠B，求证AD=BC．”时，提出了两种解答思路：
思路1：过一个顶点作另一条腰的平行线，将梯形转化为等腰三角形和平行四边形；
思路2：过同一底上的两个顶点作另一底的垂线段，将梯形转化为直角三角形和矩形；请结合以上思路，选用一种方法证明上题．

答案解析收藏纠错 + 选题
20. (2022九下·乐平期中) 为了响应市委市政府号召，全民防疫，某地市民只需携带本人身份证，即可随机选择去本市中医院（A）、第一人民医院（B）、第二人民医院（C）、第三人民医院接种疫苗（D）．
1. （1）小宇正好选择中医院接种的概率是．
2. （2）在注射第一针疫苗后21天左右需要再去注射第二针疫苗，请用树状图或列表方法表示小宇注射两针疫苗分别在不同的医院接种的概率是多少？
答案解析收藏纠错 + 选题
21. (2022·通州模拟) 2021年，我国粮食总产量再创新高．小刘同学登录国家统计局网站，查询到了我国2021年31个省、直辖市、自治区的粮食产量数据（万吨）．并对数据进行整理、描述和分析．下面给出了部分信息．
a．反映2021年我国31个省、直辖市、自治区的粮食产量数据频数分布直方图如图（数据分成8组： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）：

b.2021年我国各省、直辖市、自治区的粮食产量在 $\text{[math]}$ 这一组的是：
10928，1094.9，1231.5，1270.4，1279.9，1386.5，1421.2，1735.8，1930.3
1. （1） 2021年我国各省、直辖市、自治区粮食产量的中位数为万吨；
2. （2）小刘同学继续收集数据的过程中，发现北京市与河南省的单位面积粮食产量（千克/公顷）比较接近，如下图所示，他将自2016年至2021年北京市与河南省的单位面积粮食产量表示出来：
  （ $\text{[math]}$ ）
  
  自2016－2021年间，设北京市单位面积粮食产量的平均值为 $\text{[math]}$ ，方差为 $\text{[math]}$ ；河南省单位面积粮食产量的平均值为 $\text{[math]}$ ，方差为 $\text{[math]}$ ；则 $\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ $\text{[math]}$ （填写“”或“＜”）；
3. （3）国家统计局公布，2021年全国粮食总产量13657亿斤，比上一年增长2.0%．如果继续保持这个增长率，计算2022年全国粮食总产量约为多少亿斤（保留整数）．
答案解析收藏纠错 + 选题
22. (2022·锡山模拟) 亲爱的同学，你能利用一张矩形纸片折出大小不一的菱形吗？请你动手试一试！然后按要求完成下面问题：

已知某矩形长为8，宽为6，请你用虚线在下图中分别画出两种不同折法的菱形的示意图

并在下方横线上直接写出菱形的面积（画图特别说明： ①示意图中体现所有折痕；②菱形的顶点必须都在矩形的边上；③所画菱形是能仅用已知数据便可求出面积的图形）

答案解析收藏纠错 + 选题
23. (2022·崂山模拟) A、B两地相距19.2km，甲、乙两人相向而行，两人的运动速度保持不变。甲从A地向B地出发，当甲运动一段时间后，乙从B地向A地出发，甲、乙两人同时运动时他们之间的距离y（km）与乙运动时间t（h）满足一次函数关系式，其图象如图所示．
1. （1）根据图像求y与t的函数关系式，并求出两人的速度和；
2. （2）已知甲由A地运动到B地所用时间是乙由B地运动到A地所用时间的 $\text{[math]}$ 倍．求甲由A地运动到B地所用时间是多少小时？
答案解析收藏纠错 + 选题
24. (2022九下·诸暨月考) 图1，图2分别是某型号拉杆箱的实物图与平面示意图，具体信息如下：水平滑杆 $\text{[math]}$ 、箱长 $\text{[math]}$ 、拉杆 $\text{[math]}$ 的长度都相等，即 $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ 在线段 $\text{[math]}$ 上，点 $\text{[math]}$ 在 $\text{[math]}$ 上，支撑点 $\text{[math]}$ 到箱底 $\text{[math]}$ 的距离 $\text{[math]}$ ， $\text{[math]}$ ： $\text{[math]}$ ： $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ，请根据以上信息，解决下列问题：
1. （1）求水平滑杆 $\text{[math]}$ 的长度；
2. （2）求拉杆端点 $\text{[math]}$ 到水平滑杆 $\text{[math]}$ 的距离 $\text{[math]}$ 的值 $\text{[math]}$ 结果保留到 $\text{[math]}$ 参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
答案解析收藏纠错 + 选题
25. (2022·坪山模拟) 如图，AB是 $\text{[math]}$ 的直径，弦 $\text{[math]}$ ，E是OB的中点，连接CE并延长到点F，使 $\text{[math]}$ ，连接AF交 $\text{[math]}$ 于点D，连接BD，BF．
1. （1）求证：直线BF是 $\text{[math]}$ 的切线；
2. （2）若AF长为 $\text{[math]}$ ，求BD的长．
答案解析收藏纠错 + 选题
26. (2022·来安模拟) 已知二次函数的图象 $\text{[math]}$ 与x轴交于点 $\text{[math]}$ ， B．
1. （1）求二次函数的表达式；
2. （2）当 $\text{[math]}$ ， $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ 是实数， $\text{[math]}$ ）时，该函数对应的函数值分别为 $\text{[math]}$ ， $\text{[math]}$ ．若 $\text{[math]}$ ，试说明 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
27. (2020·宁波模拟) 数学上称“费马点”是位于三角形内且到三角形三个顶点距离之和最短的点。
现定义：菱形对角线上一点到该对角线同侧两条边上的两点距离最小的点称为类费马点。

例如：菱形ABCD，P是对角线BD上一点，E、F是边BC和CD上的两点，若点P满足PE与PF之和最小，则称点P为类费马点
1. （1）如图1，在菱形ABCD中，AB=4，点P是BD上的类费马点
  ①E为BC的中点，F为CD的中点，则PE+PF=。
  
  ②E为BC上一动点，F为CD上一动点，且∠ABC=60°则PE+PF=。
2. （2）如图2，在菱形ABCD中，AB=4，连结AC，点P是△ABC的费马点，（即PA，PB，PC之和最小），①当∠ABC=60°时，BP=▲
  ②当∠ABC=30°时，你能找到△ABC的费马点P吗？画图做简要说明，并求此时PA+PB+PC的值
答案解析收藏纠错 + 选题