

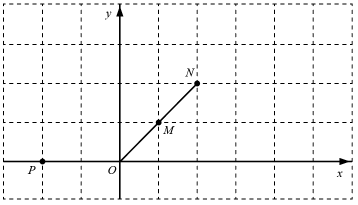
①在图中画出点;
②连接交线段
于点
求证:
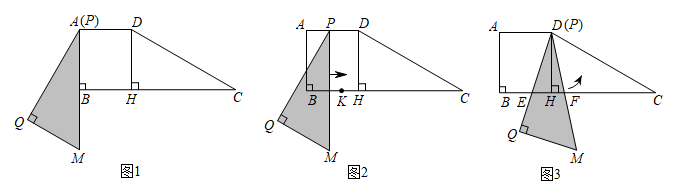
①边PQ从平移开始,到绕点D旋转结束,求边PQ扫过的面积;
②如图2,点K在BH上,且 .若△PQM右移的速度为每秒1个单位长,绕点D旋转的速度为每秒5°,求点K在△PQM区域(含边界)内的时长;
③如图3.在△PQM旋转过程中,设PQ , PM分别交BC于点E , F , 若BE=d , 直接写出CF的长(用含d的式子表示).
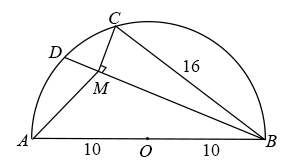
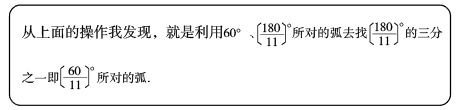
操作:如图1,分别将半圆的圆心角
(
取1、4、5、10)所对的弧三等分(要求:仅用圆规作图,不写作法,保留作图痕迹);

交流:当时,可以仅用圆规将半圆
的圆心角
所对的弧三等分吗?
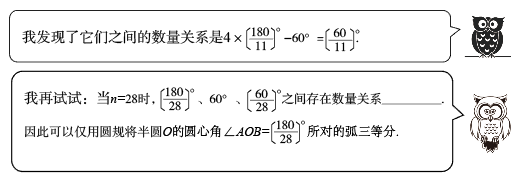
探究:你认为当满足什么条件时,就可以仅用圆规将半圆
的圆心角
所对的弧三等分?说说你的理由.
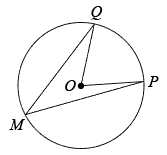
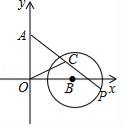
解:在网格中取格点 , 构建两个直角三角形,分别是△ABC和△CDE.
在Rt△ABC中,
在Rt△CDE中,,
所以.
所以∠=∠
.
因为∠∠
=∠
=90°,
所以∠ +∠
=90°,
所以∠ =90°,
即⊥
.