备战2023年中考数学细点逐一突破真题训练第9章二次函数的实...

更新时间：2023-03-16 浏览次数：234 类型：二轮复习

一、销售利润问题

1. (2024九下·广州开学考) 端午节前夕，某超市从厂家分两次购进 $\text{[math]}$ 、 $\text{[math]}$ 两种品牌的粽子，两次进货时，两种品牌粽子的进价不变.第一次购进 $\text{[math]}$ 品牌粽子100袋和 $\text{[math]}$ 品牌粽子150袋，总费用为7000元；第二次购进 $\text{[math]}$ 品牌粽子180袋和 $\text{[math]}$ 品牌粽子120袋，总费用为8100元.
1. （1）求 $\text{[math]}$ 、 $\text{[math]}$ 两种品牌粽子每袋的进价各是多少元；
2. （2）当 $\text{[math]}$ 品牌粽子销售价为每袋54元时，每天可售出20袋，为了促销，该超市决定对 $\text{[math]}$ 品牌粽子进行降价销售.经市场调研，若每袋的销售价每降低1元，则每天的销售量将增加5袋.当 $\text{[math]}$ 品牌粽子每袋的销售价降低多少元时，每天售出 $\text{[math]}$ 品牌粽子所获得的利润最大？最大利润是多少元？
答案解析收藏纠错 + 选题
2. (2022·黄石) 某校为配合疫情防控需要，每星期组织学生进行核酸抽样检测；防疫部门为了解学生错峰进入操场进行核酸检测情况，调查了某天上午学生进入操场的累计人数y（单位：人）与时间x（单位：分钟）的变化情况，发现其变化规律符合函数关系式： $\text{[math]}$ 数据如下表．
时间x（分钟）
0
1
2
3
…
8
$\text{[math]}$
累计人数y（人）
0
150
280
390
…
640
640
1. （1）求a，b，c的值；
2. （2）如果学生一进入操场就开始排队进行核酸检测，检测点有4个，每个检测点每分钟检测5人，求排队人数的最大值（排队人数-累计人数-已检测人数）；
3. （3）在（2）的条件下，全部学生都完成核酸检测需要多少时间？如果要在不超过20分钟让全部学生完成核酸检测，从一开始就应该至少增加几个检测点？
答案解析收藏纠错 + 选题
3. (2022·鞍山) 某超市购进一批水果，成本为8元/ $\text{[math]}$ ，根据市场调研发现，这种水果在未来10天的售价 $\text{[math]}$ （元/ $\text{[math]}$ ）与时间第 $\text{[math]}$ 天之间满足函数关系式 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ 为整数），又通过分析销售情况，发现每天销售量 $\text{[math]}$ 与时间第 $\text{[math]}$ 天之间满足一次函数关系，下表是其中的三组对应值．
时间第 $\text{[math]}$ 天
…
2
5
9
…
销售量 $\text{[math]}$
…
33
30
26
…
1. （1）求 $\text{[math]}$ 与 $\text{[math]}$ 的函数解析式；
2. （2）在这10天中，哪一天销售这种水果的利润最大，最大销售利润为多少元？
答案解析收藏纠错 + 选题
4. (2022·抚顺模拟) 为增加农民收入，助力乡村振兴.某驻村干部指导农户进行草莓种植和销售，已知草莓的种植成本为8元/千克，经市场调查发现，今年五一期间草莓的销售量y（千克）与销售单价x（元/千克）（8≤x≤40）满足的函数图象如图所示.
1. （1）根据图象信息，求y与x的函数关系式；
2. （2）求五一期间销售草莓获得的最大利润.
答案解析收藏纠错 + 选题
5. (2022·郯城模拟) 某工厂生产并销售A ， B两种型号车床共14台，生产并销售1台A型车床可以获利10万元；如果生产并销售不超过4台B型车床，则每台B型车床可以获利17万元，如果超出4台B型车床，则每超出1台，每台B型车床获利将均减少1万元．设生产并销售B型车床 $\text{[math]}$ 台．
1. （1）当 $\text{[math]}$ 时，完成以下两个问题：
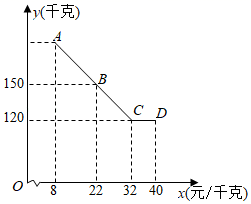
  ①请补全下面的表格：
  
  A型
  
  B型
  
  车床数量/台
  
  ▲
  
  $\text{[math]}$
  
  每台车床获利/万元
  
  10
  
  ▲
  
  ②若生产并销售B型车床比生产并销售A型车床获得的利润多70万元，问：生产并销售B型车床多少台？
2. （2）当0＜ $\text{[math]}$ ≤14时，设生产并销售A ， B两种型号车床获得的总利润为W万元，如何分配生产并销售A ， B两种车床的数量，使获得的总利润W最大？并求出最大利润．
答案解析收藏纠错 + 选题

二、抛球问题

6. (2022·新昌模拟) 一个球从地面竖直向上弹起时的速度为10m/s，经过t（s）时球的高度为h（m）.已知物体竖直上抛运动中， $\text{[math]}$ （ $\text{[math]}$ 表示物体运动上弹开始的速度，g表示重力系数，取 $\text{[math]}$ ）.
1. （1）写出h（m）关于t（s）的二次函数表达式.
2. （2）求球从弹起到最高点需要多少时间，最高点的高度是多少？
3. （3）若球在下落至 $\text{[math]}$ 处时，遇一夹板（这部分运动的函数图象如图所示），球以遇到夹板时的速度再次向上竖直弹起，然后落回地面.求球从最初10m/s弹起到落回地面的时间.
答案解析收藏纠错 + 选题
7. (2022·兰州) 掷实心球是兰州市高中阶段学校招生体育考试的选考项目．如图1是一名女生投掷实心球，实心球行进路线是一条抛物线，行进高度y（m）与水平距离x（m）之间的函数关系如图2所示，抛出时起点处高度为 $\text{[math]}$ ，当水平距离为3m时，实心球行进至最高点3m处．
1. （1）求y关于x的函数表达式；
2. （2）根据兰州市高中阶段学校招生体有考试评分标准（女生），投掷过程中，实心球从起点到落地点的水平距离大于等于6.70m，此项考试得分为满分10分．该女生在此项考试中是否得满分，请说明理由．
答案解析收藏纠错 + 选题
8. (2022·攀枝花) 第24届冬奥会（也称2022年北京冬奥会）于2022年2月4日至2月20日在中国北京举行，北京成为了历史上第一座既举办过夏奥会又举办过冬奥会的城市.冬奥会上跳台滑雪是一项极为壮观的运动.运动员经过助滑、起跳、空中飞行和着陆，整个动作连贯一致，一气呵成，如图，某运动员穿着滑雪板，经过助滑后，从倾斜角 $\text{[math]}$ 的跳台A点以速度 $\text{[math]}$ 沿水平方向跳出，若忽略空气阻力影响，水平方向速度将保持不变.同时，由于受重力作用，运动员沿竖直方向会加速下落，因此，运动员在空中飞行的路线是抛物线的一部分，已知该运动员在B点着陆， $\text{[math]}$ ，且 $\text{[math]}$ .忽略空气阻力，请回答下列问题：
1. （1）求该运动员从跳出到着陆垂直下降了多少m？
2. （2）以A为坐标原点建立直角坐标系，求该抛物线表达式；
3. （3）若该运动员在空中共飞行了4s，求他飞行2s后，垂直下降了多少m？
答案解析收藏纠错 + 选题
9. (2022·石家庄模拟) 如图1的小山丘是科研部门的小球弹射实验场地，在小山丘一侧的山坡上建有小球弹射发射装置，另一侧建有圆柱形小球接收装置，如图2为实验场地的纵截面示意图，小山丘纵截面的外部轮廓线近似为抛物线的一部分，以小山丘纵截面与地面的交线为x轴，以过发射装置所在的直线AB为y轴，建立平面直角坐标系，发射装置底部在轮廓线的点A处，距离地面为1米，在发射装置3米的点B处是发射点，已知小山丘纵截面的外部轮廓线为 $\text{[math]}$ ，从发射装置的发射点弹射一个小球（忽略空气阻力）时，小球的飞行路线为一段抛物线 $\text{[math]}$ ．
1. （1）直接写出c的值，当小球离B处的水平距离和竖直距离都为4米时，求b的值，并求小球到小山丘的竖直距离为1米时，小球离B处的水平距离；
2. （2）若小球最远着陆点到y轴的距离为15米，当小球飞行到小山丘顶的正上方，且与顶部距离不小于 $\text{[math]}$ 米时，求b的取值范围，并求小球飞行路线的顶点到x轴距离的最小值；
3. （3）圆柱形小球接收装置的最大截面为矩形CDEF，已知点E在 $\text{[math]}$ 上，其横坐标为14， $\text{[math]}$ 轴， $\text{[math]}$ ， $\text{[math]}$ ．若小球恰好落入该装置内（不触碰装置侧壁），请直接写出b的取值范围．
答案解析收藏纠错 + 选题
10. (2021·路南模拟) 如图所示，一场篮球赛中，队员甲跳起投篮，已知球出手时离地面 $\text{[math]}$ 米，与篮圈中心的水平距离为7米，当球出手的水平距离4米时到达最大高度4米，设篮球运行轨迹为抛物线，篮圈距地面3米．
1. （1）请根据图中所给的平面直角坐标系，求出篮球运行轨迹的抛物线解析式；
2. （2）问此篮球能否投中？
3. （3）此时，若对方队员乙上前盖帽，已知乙最大摸高3.19米，他如何做才有可能获得成功？（说明在球出手后，未达到最高点时，被防守队员拦截下来，称为盖帽，但球到达最高点后，处于下落过程时，防守队员再出手拦截，属于犯规，判进攻方得2分．）
答案解析收藏纠错 + 选题

三、喷泉问题

11. (2023·临潼模拟) 某游乐场的圆形喷水池中心O有一雕塑OA，从A点向四周喷水，喷出的水柱为抛物线，且形状相同.如图，以水平方向为x轴，点O为原点建立直角坐标系，点A在y轴上，x轴上的点C，D为水柱的落水点，水柱所在抛物线第一象限部分的函数表达式为 $\text{[math]}$ .
1. （1）求雕塑高OA.
2. （2）求落水点C，D之间的距离.
3. （3）若需要在OD上的点E处竖立雕塑EF， $\text{[math]}$ ， $\text{[math]}$ .问：顶部F是否会碰到水柱？请通过计算说明.
答案解析收藏纠错 + 选题
12. (2021·嵊州模拟) 某喷泉中间的喷水管 $\text{[math]}$ ，喷水点 $\text{[math]}$ 向各个方向喷射出去的水柱为形状相同的抛物线，以水平方向为 $\text{[math]}$ 轴，喷水管所在直线为 $\text{[math]}$ 轴，喷水管与地面的接触点 $\text{[math]}$ 为原点建立直角坐标系，如图所示，已知喷出的水柱距原点 $\text{[math]}$ 处达到最高，高度为 $\text{[math]}$ .
1. （1）求水柱所在抛物线（第一象限）的函数表达式.
2. （2）身高为 $\text{[math]}$ 的小明站在距离喷水管 $\text{[math]}$ 的地方，他会被水喷到吗？
3. （3）现重新改建喷泉，升高喷水管，使落水点与喷水管距离 $\text{[math]}$ ，已知喷水管升高后，喷水管喷出的水柱抛物线形状不变，且水柱仍在距离原点 $\text{[math]}$ 处达到最高，则喷水管 $\text{[math]}$ 要升高多少？
答案解析收藏纠错 + 选题
13. (2022·诸暨模拟) 如图1，一个移动喷灌架喷射出的水流可以近似地看成抛物线．图2是喷灌架为一坡地草坪喷水的平面示意图，喷水头的高度（喷水头距喷灌架底部的距离）是1米，当喷射出的水流与喷灌架的水平距离为10米时，达到最大高度6米，现将喷灌架置于坡地底部点O处，草坡上距离O的水平距离为15米处有一棵高度为1.2米的小树 $\text{[math]}$ 垂直水平地面且A点到水平地面的距离为3米．
1. （1）计算说明水流能否浇灌到小树后面的草地．
2. （2）记水流的高度为 $\text{[math]}$ ，斜坡的高度为 $\text{[math]}$ ，求 $\text{[math]}$ 的最大值．
3. （3）如果要使水流恰好喷射到小树顶端的点B ，那么喷射架应向后平移多少米？
答案解析收藏纠错 + 选题

四、拱桥问题

14. (2021八下·金华期中) 如今我国的大棚（如图1）种植技术已十分成熟.小明家的菜地上有一个长为16米的蔬菜大棚，其横截面顶部为抛物线型，大棚的一端固定在离地面高1米的墙体 $\text{[math]}$ 处，另一端固定在离地面高2米的墙体 $\text{[math]}$ 处，现对其横截面建立如图2所示的平面直角坐标系.已知大棚上某处离地面的高度 $\text{[math]}$ （米）与其离墙体 $\text{[math]}$ 的水平距离 $\text{[math]}$ （米）之间的关系满足 $\text{[math]}$ ，现测得 $\text{[math]}$ ， $\text{[math]}$ 两墙体之间的水平距离为6米.
1. （1）直接写出 $\text{[math]}$ ， $\text{[math]}$ 的值；
2. （2）求大棚的最高处到地面的距离；
3. （3）小明的爸爸欲在大棚内种植黄瓜，需搭建高为 $\text{[math]}$ 米的竹竿支架若干，已知大棚内可以搭建支架的土地平均每平方米需要4根竹竿，则共需要准备多少根竹竿？
答案解析收藏纠错 + 选题

15. (2022·丰台模拟) 某公园在人工湖里安装一个喷泉，在湖心处竖直安装一根水管，在水管的顶端安一个喷水头，水柱从喷水头喷出到落于湖面的路径形状可以看作是抛物线的一部分．若记水柱上某一位置与水管的水平距离为d米，与湖面的垂直高度为h米．下面的表中记录了d与h的五组数据：

d（米）	0	1	2	3	4
h（米）	0.5	1.25	1.5	1.25	0.5

根据上述信息，解决以下问题：

（1）在下面网格（图1）中建立适当的平面直角坐标系，并根据表中所给数据画出表示h与d函数关系的图象；
（2）若水柱最高点距离湖面的高度为m米，则m=；
（3）现公园想通过喷泉设立新的游玩项目，准备通过只调节水管露出湖面的高度，使得游船能从水柱下方通过．如图2所示，为避免游船被喷泉淋到，要求游船从水柱下方中间通过时，顶棚上任意一点到水柱的竖直距离均不小于0.5米．已知游船顶棚宽度为3米，顶棚到湖面的高度为2米，那么公园应将水管露出湖面的高度（喷水头忽略不计）至少调节到多少米才能符合要求？请通过计算说明理由（结果保留一位小数）．

答案解析收藏纠错 + 选题

16. (2022·平度模拟) 如图1是一座抛物线型拱桥，图2是其在直角坐标系中的侧面示意图．在正常水位时水面宽 $\text{[math]}$ ，此时水面离桥拱顶部的距离为 $\text{[math]}$ ．
1. （1）按如图2所示的直角坐标系，求此抛物线的函数表达式；
2. （2）如图3，因某种需要，在桥拱顶部及桥的两端树立了三根支柱 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 架设钢缆，在钢缆和桥面之间竖直悬挂若干安全绳，过相邻支柱顶端的钢缆具有相同的抛物线形状，且左、右两条抛物线关于 $\text{[math]}$ 轴对称，左面钢缆抛物线可以用 $\text{[math]}$ 表示．
  ①求左、右面两条钢缆的最低点之间的距离是多少？
  ②求安全绳长度（钢缆和桥面之间距离）的最小值是多少？
答案解析收藏纠错 + 选题
17. (2020·浙江模拟) 一隧道内设双行公路，隧道的高MN为6米.下图是隧道的截面示意图，并建立如图所示的直角坐标系，它是由一段抛物线和一个矩形CDEF的三条边围成的，矩形的长DE是8米，宽CD是2米.
1. （1）求该抛物线的解析式；
2. （2）为了保证安全，要求行驶的车辆顶部与隧道顶部至少要有0.5米的距离.若行车道总宽度PQ（居中，两边为人行道）为6米，一辆高3.2米的货运卡车（设为长方形）靠近最右边行驶能否安全？请写出判断过程；
3. （3）施工队计划在隧道门口搭建一个矩形“脚手架”ABHG，使H、G两点在抛物线上，A、B两点在地面DE上，设GH长为n米，“脚手架”三根木杆AG、GH、HB的长度之和为L，当n为何值时L最大，最大值为多少？
答案解析收藏纠错 + 选题
18. (2020·武汉模拟) 某坦克部队需要经过一个拱桥（如图所示），拱桥的轮廓是抛物线形，拱高OC＝6m，跨度AB＝20m，有5根支柱：AG、MN、CD、EF、BH，相邻两支柱的距离均为5m.
1. （1）以AB的中点为原点，AB所在直线为x轴，支柱CD所在直线为y轴，建立平面直角坐标系，求抛物线的解析式；
2. （2）若支柱每米造价为2万元，求5根支柱的总造价；
3. （3）拱桥下面是双向行车道（正中间是一条宽2m的隔离带），其中的一条行车道是坦克的行进方向，现每辆坦克长4m，宽2m，高3m，行驶速度为24km/h，坦克允许并排行驶，坦克前后左右距离忽略不计，试问120辆该型号坦克从刚开始进入到全部通过这座长1000m的拱桥隧道所需最短时间为多少分钟？
答案解析收藏纠错 + 选题