人教版初中数学几何辅助线进阶训练——构造中线（不含相似）

更新时间：2023-05-11 浏览次数：104 类型：复习试卷

一、阶段一

1. (2022八上·新昌月考) 已知：如图，在 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 边上的高线， $\text{[math]}$ 是 $\text{[math]}$ 边上的中线，G是 $\text{[math]}$ 的中点，连结 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
1. （1）求 $\text{[math]}$ 的长.
2. （2）求证： $\text{[math]}$ .
答案解析收藏纠错 + 选题
2. (2022九上·高州月考) 如图， $\text{[math]}$ 中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，线段 $\text{[math]}$ 的两个端点 $\text{[math]}$ 、 $\text{[math]}$ 分别在边 $\text{[math]}$ ， $\text{[math]}$ 上滑动，且 $\text{[math]}$ ，若点 $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ 、 $\text{[math]}$ 的中点，则 $\text{[math]}$ 的最小值为．

答案解析收藏纠错 + 选题
3. (2022八上·海曙期中)
1. （1）【问题情境】课外兴趣小组活动时，老师提出了如下问题：如图1，在△ABC中，若AB＝13，AC＝9，求BC边上的中线AD的取值范围．
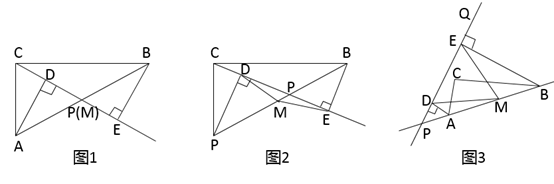
  小明在组内经过合作交流，得到了如下的解决方法：延长AD至点E，使DE＝AD，连接BE，容易证得△ADC≌△EDB，再由“三角形的三边关系”可求得AD的取值范围是．
  
  解后反思：题目中出现“中点”、“中线”等条件，可考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集中到同一个三角形之中．
2. （2）【初步运用】如图2，AD是△ABC的中线，BE交AC于E，交AD于F，且∠FAE＝∠AFE．若AE＝4，EC＝3，求线段BF的长．
3. （3）【拓展提升】如图3，在△ABC中，D为BC的中点，DE⊥DF分别交AB，AC于点E，F．求证：BE+CF＞EF．
答案解析收藏纠错 + 选题
4. (2023·东营模拟) 如图，在线段AB上取一点C，分别以AC，BC为边长作菱形BCFG和菱形ACDE，使点D在边CF上，连接EG，H是EG的中点，且 $\text{[math]}$ ，则EG的长是．

答案解析收藏纠错 + 选题
5. (2022七下·淮阴期末) 在 $\text{[math]}$ 中，已知点D、E、F分别是边AE、BF、CD上的中点，若 $\text{[math]}$ 的面积是14，则 $\text{[math]}$ 的面积为．

答案解析收藏纠错 + 选题
6. (2022八下·大荔期末) 如图， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，过C作 $\text{[math]}$ ，连接AF与BC相交于点G，若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数．

答案解析收藏纠错 + 选题
7. (2022·龙东) 如图， $\text{[math]}$ 中， $\text{[math]}$ ， AD平分 $\text{[math]}$ 与BC相交于点D，点E是AB的中点，点F是DC的中点，连接EF交AD于点P．若 $\text{[math]}$ 的面积是24， $\text{[math]}$ ，则PE的长是（）

A . 2.5 B . 2 C . 3.5 D . 3

答案解析收藏纠错 + 选题
8. (2022八下·黄冈期中) 如图所示，E是边长为1的正方形ABCD的对角线BD上一点，且BE=BC，P为CE上任意一点，PQ⊥BC于点Q，PR⊥BE于点R，则PQ+PR的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022八下·江都期中) 如图，在平行四边形ABCD中，BC＝2AB，CE⊥AB于E，F为AD的中点，若∠AEF＝54°，则∠B＝（）

A . 54° B . 60° C . 66° D . 72°

答案解析收藏纠错 + 选题
10. (2021七下·历下期中)
1. （1）方法学习：数学兴趣小组活动时，张老师提出了如下问题：如图1，在△ABC中，AB＝8，AC＝6，求BC边上的中线AD的取值范围．小明在组内经过合作交流，得到了如下的解决方法（如图2），
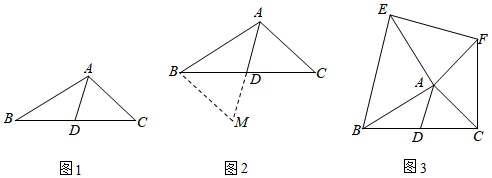
  ①延长AD到M，使得DM＝AD；
  ②连接BM，通过三角形全等把AB、AC、2AD转化在△ABM中；
  ③利用三角形的三边关系可得AM的取值范围为AB﹣BM＜AM＜AB+BM，从而得到AD的取值范围是多少；
2. （2）请你写出图2中AC与BM的数量关系和位置关系，并加以证明．
3. （3）深入思考：如图3，AD是△ABC的中线，AB＝AE，AC＝AF，∠BAE＝∠CAF＝90°，请直接利用（2）的结论，试判断线段AD与EF的数量关系，并加以证明．
答案解析收藏纠错 + 选题

二、阶段二

11. (2023·泗洪模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ .将 $\text{[math]}$ 绕顶点C旋转得到 $\text{[math]}$ ，若点O是 $\text{[math]}$ 中点，点P是 $\text{[math]}$ 中点，在旋转过程中，线段 $\text{[math]}$ 的最大值等于（）

A . 4 B . 6 C . 8 D . 10

答案解析收藏纠错 + 选题
12. (2023八上·绍兴期末) 如图1，在 $\text{[math]}$ 中， $\text{[math]}$ 分别是 $\text{[math]}$ 边上的高线，M，N分别是线段 $\text{[math]}$ 的中点.
1. （1）求证： $\text{[math]}$ .
2. （2）连接 $\text{[math]}$ ，猜想 $\text{[math]}$ 与 $\text{[math]}$ 之间的关系，并说明理由.
3. （3）若将锐角三角形 $\text{[math]}$ 变为钝角三角形 $\text{[math]}$ ，其余条件不变，如图2，直接写出 $\text{[math]}$ 与 $\text{[math]}$ 之间的关系.
答案解析收藏纠错 + 选题
13. (2023八上·巴东月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 为 $\text{[math]}$ 边的中线，E为 $\text{[math]}$ 上一点，连接 $\text{[math]}$ 并延长交 $\text{[math]}$ 于点F，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为.

答案解析收藏纠错 + 选题
14. (2023八上·德州月考) 如图， $\text{[math]}$ 的面积为12，点D，E，F分别为 $\text{[math]}$ 的中点，则阴影部分的面积为（）

A . 2 B . 3 C . 4 D . 6

答案解析收藏纠错 + 选题
15. (2022八上·杭州期中) 如图，在△ABC中，AB＝AC＝5，BC＝6，D，E分别为线段AB，AC上一点，且AD＝AE，连接BE、CD交于点G，延长AG交BC于点F.以下四个结论正确的是（）
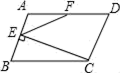
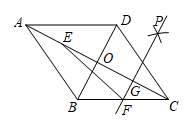
①BF＝CF；②若BE⊥AC，则CF＝DF；③若BE平分∠ABC，则FG＝ $\text{[math]}$ ；④连结EF，若BE⊥AC，则∠DFE＝2∠ABE.

A . ①②③ B . ③④ C . ①②④ D . ①②③④

答案解析收藏纠错 + 选题
16. (2022八上·新城月考) 阅读理解：亲爱的同学们，在以后的学习中我们会学习一个定理：直角三角形斜边上的中线等于斜边的一半．即：如图1：在 $\text{[math]}$ 中， $\text{[math]}$ ，若点 $\text{[math]}$ 是斜边 $\text{[math]}$ 的中点，则 $\text{[math]}$ ．
1. （1）牛刀小试：在图1中，若 $\text{[math]}$ ， $\text{[math]}$ ，其他条件不变，则 $\text{[math]}$ ；
2. （2）活学活用：如图2，已知 $\text{[math]}$ ，点 $\text{[math]}$ 、 $\text{[math]}$ 分别为 $\text{[math]}$ 、 $\text{[math]}$ 的中点， $\text{[math]}$ ， $\text{[math]}$ ．求 $\text{[math]}$ 的长；
3. （3）问题解决：为了提高全民健身环境，公园管理部门想要建一个形状如图3中的四边形 $\text{[math]}$ ，其中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 千米，要在公园的 $\text{[math]}$ 、 $\text{[math]}$ 之间铺设一条笔直的塑胶跑道，若跑道铺设成本每米200元，当 $\text{[math]}$ 最大时，请问管理部门预算160万元够用吗？
答案解析收藏纠错 + 选题
17. (2022八下·元阳期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 于点D， $\text{[math]}$ 于点E，AD与CE相交于点F，连接DE．
1. （1）若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ ．
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
18. (2022八下·黄山期末) 如图，菱形ABCD的边长是4，∠A=60°，点G为AB的中点，以BG为边作菱形BEFG，其中点E在CB的延长线上，点P为FD的中点，连接PB．则PB=．

答案解析收藏纠错 + 选题
19. (2022·七星关模拟) 如图，在菱形ABCD中，对角线AC，BD相交于点O，点E，F分别是AO，BC的中点，连接EF.按以下步骤作图：①分别以点O，C为圆心，大于 $\text{[math]}$ OC的长为半径作弧，两弧交于点P；②作直线PF，交AC于点G.若AD＝4 $\text{[math]}$ ， BD＝8，则线段EF的长为 .

答案解析收藏纠错 + 选题
20. (2022·海曙模拟) 如图，在平行四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 的中点，连结 $\text{[math]}$ ， $\text{[math]}$ ，下列结论：① $\text{[math]}$ ，② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ，其中正确结论的个数共有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

三、阶段三

21. (2023八下·杭州月考) 在平行四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 中点，点 $\text{[math]}$ 在线段 $\text{[math]}$ 上，连接 $\text{[math]}$ ，在 $\text{[math]}$ 下方有一点 $\text{[math]}$ ，满足 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的面积；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求证： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
22. (2023八下·南宁月考)
1. （1）【探究发现】（1）如图1， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 的中点， $\text{[math]}$ 、 $\text{[math]}$ 分别为边 $\text{[math]}$ 、 $\text{[math]}$ 上两点，若满足 $\text{[math]}$ ，则 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间满足的数量关系是.
2. （2）【类比应用】如图2， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 的中点， $\text{[math]}$ 、 $\text{[math]}$ 分别为边 $\text{[math]}$ 、 $\text{[math]}$ 上两点，若满足 $\text{[math]}$ ，试探究 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间满足的数量关系，并说明理由.
3. （3）【拓展延伸】在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 的中点， $\text{[math]}$ 、 $\text{[math]}$ 分别为直线 $\text{[math]}$ 、 $\text{[math]}$ 上两点，若满足 $\text{[math]}$ ， $\text{[math]}$ ，请直接写出 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
23. (2023九下·姑苏开学考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， AB＝AC＝5，点 $\text{[math]}$ 在 $\text{[math]}$ 上，且 $\text{[math]}$ ，点E是AB上的动点，连结 $\text{[math]}$ ，点 $\text{[math]}$ ， G分别是BC，DE的中点，连接 $\text{[math]}$ ， $\text{[math]}$ ，当AG＝FG时，线段 $\text{[math]}$ 长为

答案解析收藏纠错 + 选题
24. (2022八上·金东月考) 如图，在Rt△ABC中，C为直角顶点，∠ABC＝20°，O为斜边的中点，将OA绕着点O逆时针旋转θ°（0＜θ＜180）至OP，当△BCP恰为轴对称图形时，θ的值为．

答案解析收藏纠错 + 选题
25. (2022·灞桥模拟) 在菱形ABCD中，∠D=60°，CD=4，E为菱形内部一点，且AE=2，连接CE，点F为CE中点，连接BF，取BF中点G，连接AG，则AG的最大值为.

答案解析收藏纠错 + 选题
26. (2022八下·温岭期中) 如图，菱形ABCD的对角线AC，BD相交于点O，过点A作AH⊥BC于点H，连接OH，若OB＝4.5，S_菱形ABCD＝36，则OH的长为（）

A . 3 B . 3.5 C . 4 D . 4.5

答案解析收藏纠错 + 选题
27. (2022八下·杭州期中) 点P是平行四边形 $\text{[math]}$ 的对角线 $\text{[math]}$ 所在直线上的一个动点（点P不与点A、C重合），分别过点A、C向直线 $\text{[math]}$ 作垂线，垂足分别为点E、F.点O为 $\text{[math]}$ 的中点.
1. （1）如图1，当点P与点O重合时，线段 $\text{[math]}$ 和 $\text{[math]}$ 的关系是；
2. （2）当点P运动到如图2所示的位置时，请证明（1）中的结论仍然成立.
3. （3）如图3，点P在线段 $\text{[math]}$ 的延长线上运动，当 $\text{[math]}$ 时，试探究线段 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间的关系.
答案解析收藏纠错 + 选题
28. (2021·太原模拟) 综合与实践
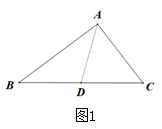
问题背景：数学小组在一次课外学习交流时，组内一同学提出如下问题：在 $\text{[math]}$ 中， $\text{[math]}$ ，D为 $\text{[math]}$ 边上一点，但不与点B，点C重合，过点D作 $\text{[math]}$ 于点E．连接 $\text{[math]}$ ，M为 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）观察发现：如图1， $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系是；
2. （2）思考分享：如图2，将 $\text{[math]}$ 绕点B顺时针旋转，其他条件不变，则（1）中的结论还成立，请证明．小明是这样思考的：延长 $\text{[math]}$ 至点 $\text{[math]}$ ，使得 $\text{[math]}$ ，连接 $\text{[math]}$ 运用三角形中位线定理，…．按照他的思路或采用其他方法证明；
3. （3）探究计算：若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，在 $\text{[math]}$ 绕点B旋转一周的过程中，当直线 $\text{[math]}$ 经过点A时，线段 $\text{[math]}$ 的长为．
答案解析收藏纠错 + 选题
29. (2021八上·万州期末) 已知，点P是Rt△ABC斜边AB上一动点（不与A、B重合），分别过A、B向直线CP作垂线，垂足分别为D、E，M为斜边AB的中点（备注，可以直接用结论：直角三角形斜边上的中线等于斜边的一半）.
1. （1）如图1，当点P与点M重合时，AD与BE的位置关系是，MD与ME的数量关系是.
2. （2）如图2，当点P在线段AB上不与点M重合时，试判断MD与ME的数量关系，并说明理由；
3. （3）如图3，当点P在线段BA的延长线上且PQ是不与AB重合的任一直线时，分别过A、B向直线PQ作垂线，垂足分别为D、E，此时（2）中的结论是否成立？若成立，请说明理由.
答案解析收藏纠错 + 选题
30. (2021九上·连山期末) 在 $\text{[math]}$ 与 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，连接 $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ， $\text{[math]}$ 绕着点 $\text{[math]}$ 旋转.
1. （1）如图1，当点 $\text{[math]}$ 落在 $\text{[math]}$ 的延长线上时， $\text{[math]}$ 与 $\text{[math]}$ 的数量关系是：；
2. （2）如图2，当 $\text{[math]}$ 旋转到点 $\text{[math]}$ 落在 $\text{[math]}$ 的延长线上时， $\text{[math]}$ 与 $\text{[math]}$ 是否仍有具有（1）中的数量关系，如果具有，请给予证明；如果没有，请说明理由；
3. （3）旋转过程中，若当 $\text{[math]}$ 时，直接写出 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题