备考2023年中考数学压轴题训练 ——解直角三角形

更新时间：2023-05-14 浏览次数：147 类型：三轮冲刺

一、真题

1. (2022·连云港) 如图

【问题情境】

在一次数学兴趣小组活动中，小昕同学将一大一小两个三角板按照如图1所示的方式摆放.其中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .

【问题探究】

小昕同学将三角板 $\text{[math]}$ 绕点 $\text{[math]}$ 按顺时针方向旋转.
1. （1）如图2，当点 $\text{[math]}$ 落在边 $\text{[math]}$ 上时，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，求 $\text{[math]}$ 的长.
2. （2）若点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 在同一条直线上，求点 $\text{[math]}$ 到直线 $\text{[math]}$ 的距离.
3. （3）连接 $\text{[math]}$ ，取 $\text{[math]}$ 的中点 $\text{[math]}$ ，三角板 $\text{[math]}$ 由初始位置（图1），旋转到点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 首次在同一条直线上（如图3），求点 $\text{[math]}$ 所经过的路径长.
4. （4）如图4， $\text{[math]}$ 为 $\text{[math]}$ 的中点，则在旋转过程中，点 $\text{[math]}$ 到直线 $\text{[math]}$ 的距离的最大值是.
答案解析收藏纠错 + 选题
2. (2022·重庆) 如图，在锐角△ABC中，∠A=60°，点D，E分别是边AB，AC上一动点，连接BE交直线CD于点F．
1. （1）如图1，若AB>AC，且BD=CE，∠BCD=∠CBE，求∠CFE的度数；
2. （2）如图2，若AB=AC，且BD=AE，在平面内将线段AC绕点C顺时针方向旋转60°得到线段CM，连接MF，点N是MF的中点，连接CN．在点D，E运动过程中，猜想线段BF，CF，CN之间存在的数量关系，并证明你的猜想；
3. （3）若AB=AC，且BD=AE，将△ABC沿直线AB翻折至△ABC所在平面内得到△ABP，点H是AP的中点，点K是线段PF上一点，将△PHK沿直线HK翻折至△PHK所在平面内得到△QHK，连接PQ．在点D，E运动过程中，当线段PF取得最小值，且QK⊥PF时，请直接写出 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
3. (2022·攀枝花) 如图，直线 $\text{[math]}$ 分别与x轴、y轴交于点A、B，点C为线段 $\text{[math]}$ 上一动点（不与A、B重合），以C为顶点作 $\text{[math]}$ ，射线 $\text{[math]}$ 交线段 $\text{[math]}$ 于点D，将射线 $\text{[math]}$ 绕点O顺时针旋转 $\text{[math]}$ 交射线 $\text{[math]}$ 于点E，连接 $\text{[math]}$ .
1. （1）证明： $\text{[math]}$ ；（用图1）
2. （2）当 $\text{[math]}$ 为直角三角形时，求 $\text{[math]}$ 的长度；（用图2）
3. （3）点A关于射线 $\text{[math]}$ 的对称点为F，求 $\text{[math]}$ 的最小值.（用图3）
答案解析收藏纠错 + 选题
4. (2023·博山模拟) 在数学兴趣小组活动中，同学们对菱形的折叠问题进行了探究.如图（1），在菱形 $\text{[math]}$ 中， $\text{[math]}$ 为锐角， $\text{[math]}$ 为 $\text{[math]}$ 中点，连接 $\text{[math]}$ ，将菱形 $\text{[math]}$ 沿 $\text{[math]}$ 折叠，得到四边形 $\text{[math]}$ ，点 $\text{[math]}$ 的对应点为点 $\text{[math]}$ ，点 $\text{[math]}$ 的对应点为点 $\text{[math]}$ .
1. （1）【观察发现】 $\text{[math]}$ 与 $\text{[math]}$ 的位置关系是；
2. （2）【思考表达】连接 $\text{[math]}$ ，判断 $\text{[math]}$ 与 $\text{[math]}$ 是否相等，并说明理由；
3. （3）如图（2），延长 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，请探究 $\text{[math]}$ 的度数，并说明理由；
4. （4）【综合运用】如图（3），当 $\text{[math]}$ 时，连接 $\text{[math]}$ ，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，请写出 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间的数量关系，并说明理由.
答案解析收藏纠错 + 选题
5. (2023·遵义模拟) 如图1，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 边上的一点，连接 $\text{[math]}$ ，将矩形 $\text{[math]}$ 沿 $\text{[math]}$ 折叠，顶点 $\text{[math]}$ 恰好落在 $\text{[math]}$ 边上的点 $\text{[math]}$ 处，延长 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ．
1. （1）求线段 $\text{[math]}$ 的长；
2. （2）求证四边形 $\text{[math]}$ 为菱形；
3. （3）如图2， $\text{[math]}$ ， $\text{[math]}$ 分别是线段 $\text{[math]}$ ， $\text{[math]}$ 上的动点（与端点不重合），且 $\text{[math]}$ ，设 $\text{[math]}$ ，是否存在这样的点 $\text{[math]}$ ，使 $\text{[math]}$ 是直角三角形？若存在，请求出 $\text{[math]}$ 的值；若不存在，请说明理由．
答案解析收藏纠错 + 选题
6. (2022·绵阳) 如图，平行四边形ABCD中，DB＝ $\text{[math]}$ ， AB＝4，AD＝2，动点E，F同时从A点出发，点E沿着A→D→B的路线匀速运动，点F沿着A→B→D的路线匀速运动，当点E，F相遇时停止运动．
1. （1）如图1，设点E的速度为1个单位每秒，点F的速度为4个单位每秒，当运动时间为 $\text{[math]}$ 秒时，设CE与DF交于点P，求线段EP与CP长度的比值；
2. （2）如图2，设点E的速度为1个单位每秒，点F的速度为 $\text{[math]}$ 个单位每秒，运动时间为x秒，ΔAEF的面积为y，求y关于x的函数解析式，并指出当x为何值时，y的值最大，最大值为多少？
3. （3）如图3，H在线段AB上且AH＝ $\text{[math]}$ HB，M为DF的中点，当点E、F分别在线段AD、AB上运动时，探究点E、F在什么位置能使EM＝HM．并说明理由．
答案解析收藏纠错 + 选题

二、模拟预测

7. (2023·包头模拟) 阅读下面的材料，并回答所提出的问题：如图所示，在锐角三角形 $\text{[math]}$ 中，求证： $\text{[math]}$
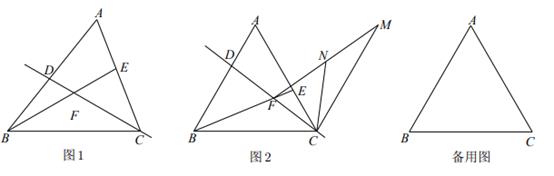
这个三角形不是一个直角三角形，不能直接使用锐角三角函数的知识去处理，所以必须构造直角三角形，过点A作 $\text{[math]}$ ，垂足为D，则在 $\text{[math]}$ 和 $\text{[math]}$ 中由正弦定义可完成证明．
解：如图，过点A作 $\text{[math]}$ ，垂足为D，
在 $\text{[math]}$ 中， $\text{[math]}$ ，则 $\text{[math]}$
$\text{[math]}$ 中， $\text{[math]}$ ，则 $\text{[math]}$
所以 $\text{[math]}$ ，即 $\text{[math]}$
1. （1）在上述分析证明过程中，主要用到了下列三种数学思想方法的哪一种（　　）
  
  A . 数形结合的思想； B . 转化的思想； C . 分类的思想
2. （2）用上述思想方法解答下面问题．
  在 $\text{[math]}$ 中， $\text{[math]}$ ，求 $\text{[math]}$ 和 $\text{[math]}$ 的面积．
3. （3）用上述结论解答下面的问题（不必添加辅助线）
  在锐角三角形 $\text{[math]}$ 中， $\text{[math]}$ ，求 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题
8. (2022·抚州模拟) 在数学学习过程中，我们总是从一些最简单的图形出发，研究其中的边角关系，然后再应用所得到的结论去解决其他较复杂的问题．
1. （1）【基本图形】如图（1），在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ．（用含m， $\text{[math]}$ 的式子表示）
2. （2）【解决问题】在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
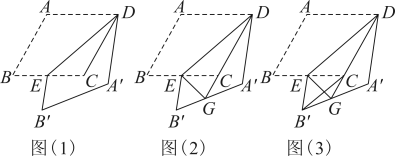
  ①如图（2），P是 $\text{[math]}$ 边上一动点，点P关于 $\text{[math]}$ ， $\text{[math]}$ 的对称点分别是D，E，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，请写出 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系，并说明理由；
  ②如图（3），若P，Q，R分别是边 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 上的动点，则 $\text{[math]}$ 的周长的最小值为 ▲ ．
3. （3）【应用拓展】如图（4），E，F分别是边长为 $\text{[math]}$ 的正方形 $\text{[math]}$ 的边 $\text{[math]}$ ， $\text{[math]}$ 上的动点，且 $\text{[math]}$ ， P，Q，R分别是△ $\text{[math]}$ 的边 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 上的动点，请直接写出 $\text{[math]}$ 的周长的最小值．
答案解析收藏纠错 + 选题
9. (2023·河南模拟) 已知：⊙O是△ABC的外接圆，连接BO并延长交AC于点D，∠CDB＝3∠ABD.
1. （1）如图1，求证：AC＝AB；
2. （2）如图2，点E是弧AB上一点，连接CE，AF⊥CE于点F，且∠BAF＝∠ACE，求tan∠BCE的值；
3. （3）如图3，在（2）的条件下，延长BD交⊙O于点H，连接FH，若EF＝2，BC＝8 $\text{[math]}$ ，求线段FH的长.
答案解析收藏纠错 + 选题
10. (2022·兴城模拟) 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点D，E在线段 $\text{[math]}$ 上 $\text{[math]}$ ，点F在 $\text{[math]}$ 的延长线上，连接CD，EF， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）如图1，当 $\text{[math]}$ 时，线段 $\text{[math]}$ 的数量关系是；
2. （2）如图2，当 $\text{[math]}$ 时，请写出线段 $\text{[math]}$ 的数量关系，并说明理由；
3. （3）在（2）的条件下，当 $\text{[math]}$ ，点E是 $\text{[math]}$ 中点时，请直接写出 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题
11. (2023·青岛模拟) 如图

【问题提出】

正多边形内任意一点到各边距离之和与这个正多边形的半径 $\text{[math]}$ 和中心角有什么关系？

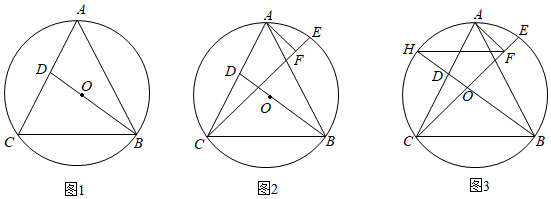
【问题探究】

如图①， $\text{[math]}$ 是等边三角形，半径 $\text{[math]}$ ， $\text{[math]}$ 是中心角， $\text{[math]}$ 是 $\text{[math]}$ 内任意一点， $\text{[math]}$ 到 $\text{[math]}$ 各边距离 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 分别为 $\text{[math]}$ ，设 $\text{[math]}$ 的边长是 $\text{[math]}$ ，面积为 $\text{[math]}$ ．过点 $\text{[math]}$ 作 $\text{[math]}$ ．

∴ $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，

∴ $\text{[math]}$ ， ①

∵ $\text{[math]}$ 又可以表示 $\text{[math]}$ ②

联立①②得 $\text{[math]}$

∴ $\text{[math]}$

∴ $\text{[math]}$
1. （1）【问题解决】
  如图②，五边形 $\text{[math]}$ 是正五边形，半径 $\text{[math]}$ ， $\text{[math]}$ 是中心角， $\text{[math]}$ 是五边形 $\text{[math]}$ 内任意一点， $\text{[math]}$ 到五边形 $\text{[math]}$ 各边距 $\text{[math]}$ 分别为 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，参照（1）的分析过程，探究 $\text{[math]}$ 的值与正五边形 $\text{[math]}$ 的半径 $\text{[math]}$ 及中心角的关系．
2. （2）【性质应用】
  正六边形（半径是 $\text{[math]}$ ）内任意一点 $\text{[math]}$ 到各边距离之和 $\text{[math]}$ ．
3. （3）如图③，正 $\text{[math]}$ 边形（半径是 $\text{[math]}$ ）内任意一点 $\text{[math]}$ 到各边距离之和 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
12. (2023·汨罗模拟) 如图①，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， D为 $\text{[math]}$ 的中点， $\text{[math]}$ 为 $\text{[math]}$ 的中位线，四边形 $\text{[math]}$ 为 $\text{[math]}$ 的内接矩形（矩形的四个顶点均在 $\text{[math]}$ 的边上）.
1. （1）计算矩形 $\text{[math]}$ 的面积；
2. （2）将矩形 $\text{[math]}$ 沿 $\text{[math]}$ 向右平移、点F落在 $\text{[math]}$ 上时停止移动，在平移过程中，当矩形与 $\text{[math]}$ 重叠部分的面积为 $\text{[math]}$ 时，求矩形平移的距离；
3. （3）如图③，将（2）中矩形平移停止时所得的矩形记为矩形 $\text{[math]}$ ，将矩形 $\text{[math]}$ 绕 $\text{[math]}$ 点按顺时针方向旋转，当H₁落在 $\text{[math]}$ 上时停止转动，旋转后的矩形记为矩形 $\text{[math]}$ ，设旋转角为 $\text{[math]}$ ，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
13. (2022·莲湖模拟)
1. （1）问题提出：如图1，在 $\text{[math]}$ 中，点 $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ 、 $\text{[math]}$ 的中点，连接 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ ；
2. （2）问题探究：如图2，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 上一点（可与端点重合），连接 $\text{[math]}$ 、 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 面积的最小值；
3. （3）问题解决：某湿地公园拟建一个梯形花园 $\text{[math]}$ ，示意图如图3所示，其中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .管理员计划在 $\text{[math]}$ 区域种植水生植物，在 $\text{[math]}$ 区域种植甲种花卉.根据设计要求，要满足点 $\text{[math]}$ 在 $\text{[math]}$ 上， $\text{[math]}$ ， $\text{[math]}$ 是锐角，且 $\text{[math]}$ ，若种植水生植物每平方米需400元，种植甲种花卉每平方米需100元，求种植水生植物和种植甲种花卉所需总费用至少为多少元？
答案解析收藏纠错 + 选题
14. (2022·榆次模拟) 综合与实践
问题背景：
在综合与实践课上，老师让同学们探索有一组邻边相等，一组对角互补的四边形的性质．如图1，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）实践操作：
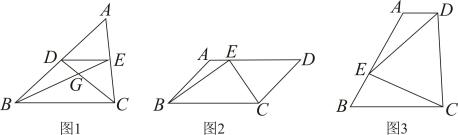
  同学们首先从特殊情形开始探索，如图2，当 $\text{[math]}$ 时，其它条件不变，发现了 $\text{[math]}$ 平分 $\text{[math]}$ 的性质，有两个小组给出如下的证明思路：
  “团结组”：利用“在一个角的内部，到角的两边距离相等的点在这个角的平分线上”；
  “实践组”：由 $\text{[math]}$ 想到将 $\text{[math]}$ 绕点 $\text{[math]}$ 旋转，使 $\text{[math]}$ 与 $\text{[math]}$ 重合，将四边形 $\text{[math]}$ 转化成我们学过的特殊图形．
  ①请你分别在图2，图3中画出符合“团结组”和“实践组”思路的辅助线；
  ②求证： $\text{[math]}$ 平分 $\text{[math]}$ ；（从上面的两个思路中选一个或按照自己的思路）
2. （2） “创新组”的同学发现在图2中 $\text{[math]}$ ，请你说明理由；
3. （3）拓展延伸：
  “善思组”的同学受“创新组”同学的启发，提出如下问题：如图4，当 $\text{[math]}$ 时，其它条件不变，延长 $\text{[math]}$ 到点 $\text{[math]}$ ，使 $\text{[math]}$ ，过点 $\text{[math]}$ 分别作 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，若 $\text{[math]}$ ，则四边形 $\text{[math]}$ 的形状为，四边形 $\text{[math]}$ 的面积为．
答案解析收藏纠错 + 选题
15. (2022·石家庄模拟) 在半径为10的扇形AOB中， $\text{[math]}$ ，延长OB到点C，使 $\text{[math]}$ ．点D为 $\text{[math]}$ 上的动点，点E是扇形所在平面内的点，连接OD，DE，EC，当 $\text{[math]}$ 时，解答下列问题：
1. （1）论证：如图1，连接OE，DC，当 $\text{[math]}$ 时，求证： $\text{[math]}$ ；
2. （2）发现：当 $\text{[math]}$ 时，∠ODE的度数可能是多少？
3. （3）尝试：如图2，当点D，E，C三点共线时，求点D到OA所在直线的距离；
4. （4）拓展：当点E在OC的下方，且DE与 $\text{[math]}$ 相切时，直接写出∠DOC的余弦值．
答案解析收藏纠错 + 选题