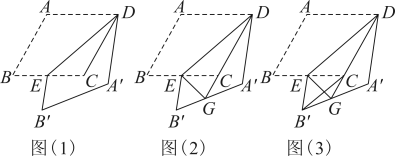
求证:四边形为菱形.
①平分
、
, ②
、
互相平分,③
, ④
、
、
、
四点共圆.
当点正好落在
边上时,在图①中画出
的轴对称图形
, 并判断四边形
的形状是 ▲ ;
如图②,当点是线段
中点,且
时,求
的长;
如图③,当点、
、
在同一直线上,且
时,求
的长.
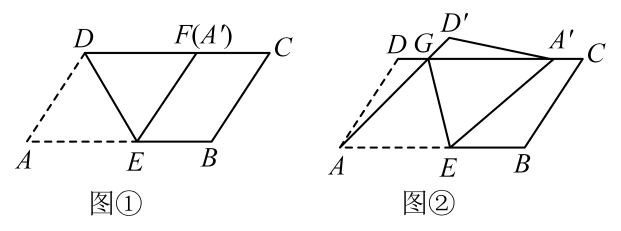
【操作感知】
第一步:对折矩形纸片 , 使
与
重合,得到折痕
, 把纸片展开.
第二步;再一次折叠纸片,使点落在
上,并使折痕经过点
, 得到折痕
, 同时得到线段
(如图1).

将正方形纸片按照
操作感知
的方式操作,并延长
交
于点
, 连接
.当点
在
上时,
, 求正方形的边长.
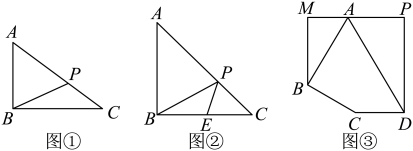
如图①,在中,
,
,
, 若P是边
上一点,则
的最小值为.
如图②,在中,
, 斜边
的长为
, E是
的中点,P是边
上一点,试求
的最小值.
某城区有一个五边形空地(
,
),城建部门计划利用该空地建造一个居民户外活动广场,其中
的部分规划为观赏区,用于种植各类鲜花,
部分规划为音乐区,供老年合唱团排练合唱或广场舞使用,四边形
部分为市民健身广场,如图③所示.已知
米,
米,
,
.为了进一步提升服务休闲功能,满足市民游园和健身需求,现要在
,
上分别取点E,F,铺设一条由
,
,
连接而成的步行景观道,已知铺设景观道的成本为100元/米,求铺设完这条步行景观道所需的最低成本.
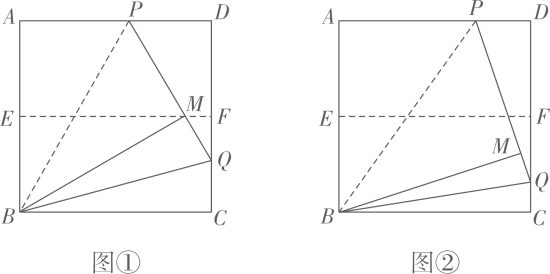
操作:
操作一:对折正方形纸片 , 使
与
重合,得到折痕
, 把纸片展平;
操作二:在上选一点P,沿
折叠,使点A落在正方形内部点M处,把纸片展平,连接
, 延长
交
于点Q,连接
.
①如图①,当点M在上时,
▲
.
②改变点P在上的位置(点P不与点A、D重合),如图②,判断
与
的数量关系,并说明理由.
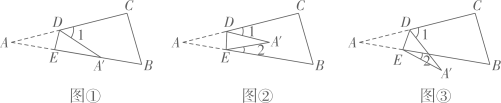
【感知】如图①,点A落在四边形BCDE的边BE上,则∠A与∠1之间的数量关系是 ▲ ;
【探究】如图②,若点A落在四边形BCDE的内部,则∠A与∠1+∠2之间存在怎样的数量关系?并说明理由.
【拓展】如图③,点A落在四边形BCDE的外部,若∠1=80°,∠2=24°,则∠A的大小为 ▲ .
已知点 ,
.