浙教版数学九年级知识点复习——二次函数、圆（含九下圆知识点）

更新时间：2023-05-20 浏览次数：39 类型：期末考试

一、单选题

1. (2023九上·澄城期末) 二次函数 $\text{[math]}$ 的部分图象如图所示，图象过点 $\text{[math]}$ ，对称轴为直线 $\text{[math]}$ ，下列结论：
（ $\text{[math]}$ ） $\text{[math]}$ ；（ $\text{[math]}$ ） $\text{[math]}$ ；（ $\text{[math]}$ ） $\text{[math]}$ ；（ $\text{[math]}$ ）若点 $\text{[math]}$ ，点 $\text{[math]}$ ，点 $\text{[math]}$ 在该函数图象上，则 $\text{[math]}$ ；（ $\text{[math]}$ ）若方程 $\text{[math]}$ 的两根为 $\text{[math]}$ 和 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ ．

其中正确的结论有（）

A . 2个 B . 3个 C . 4个 D . 5个

答案解析收藏纠错 + 选题
2. (2022九上·东阳月考) 已知二次函数y＝ax²+bx+c（a≠0）的对称轴为直线x＝-1，与x轴的一个交点B的坐标为（1，0）其图象如图所示，下列结论：①abc＜0； ②2a-b＝0； ③一元二次方程ax²+bx+c＝0的两个根是-3和1；④当y＞0时，-3＜x＜1；⑤当x＞0时，y随x的增大而增大；⑥若点E（-4，y₁），F（-2，y₂），M（3，y₃）是函数图象上的三点，则y₁＞y₂＞y₃ ，其中正确的有（）个

A . 5 B . 4 C . 3 D . 2

答案解析收藏纠错 + 选题
3. (2023九上·阳新期末) 二次函数 $\text{[math]}$ （a，c为常数且 $\text{[math]}$ ）经过 $\text{[math]}$ ，且 $\text{[math]}$ ，下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③若关于x的方程 $\text{[math]}$ 有整数解，则符合条件的p的值有3个；④当 $\text{[math]}$ 时，二次函数的最大值为c，则 $\text{[math]}$ .其中一定正确的有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
4. (2022九上·泸县月考) 如图是二次函数 $\text{[math]}$ 图象的一部分，图象过点 $\text{[math]}$ ，对称轴为直线 $\text{[math]}$ ， ① $\text{[math]}$ ② $\text{[math]}$ ③当 $\text{[math]}$ 时， $\text{[math]}$ ④若 $\text{[math]}$ ， $\text{[math]}$ 为函数图象上的两点，则 $\text{[math]}$ ，以上结论中正确的有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
5. (2022九上·新抚月考) 二次函数 $\text{[math]}$ 的部分图像如图，图像过点 $\text{[math]}$ ，对称轴为直线 $\text{[math]}$ ，下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ；⑤当 $\text{[math]}$ 时， $\text{[math]}$ 的值随 $\text{[math]}$ 值的增大而增大．其中正确的结论有（）

A . 2个 B . 3个 C . 4个 D . 5个

答案解析收藏纠错 + 选题
6. (2022九上·温州月考) 如图，已知点C是线段AB的中点，CD⊥AB且CD＝ $\text{[math]}$ AB＝a，延长CB至E，使得BE＝b，以CD，CE为边作矩形CEFD，连接并延长DB，交FE的延长线于点G，连接AG，《几何原本》中利用该图解释了代数式（2a+b）²+b²＝2[（a+b）²+a²]的几何意义，以AG为直径作圆，交AF于点H，若a＝9，b＝6，则HG的长为（）

A . 5 $\text{[math]}$ B . 18 C . 3 $\text{[math]}$ D . 17

答案解析收藏纠错 + 选题
7. (2022九上·庆云期中) 如图，点A、B分别在x轴、y轴上（ $\text{[math]}$ ）；以 $\text{[math]}$ 为直径的圆经过原点O，C是 $\text{[math]}$ 的中点，连结 $\text{[math]}$ ， $\text{[math]}$ ．下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的面积等于5；④若 $\text{[math]}$ ，则点C的坐标是 $\text{[math]}$ ，其中正确的结论有（　　）

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题
8. (2022九上·镇海区期中) 如图，在给定的锐角三角形ABC中，∠BAC=60°，D是边BC上的一个动点，以AD为直径作⊙O分别交边AB，AC于点E，F，连接EF，当点D从点B运动到点C的过程中，线段EF的长度的大小变化情况是（　　）

A . 一直不变 B . 一直减少 C . 先减小后增大 D . 先增大后减小

答案解析收藏纠错 + 选题
9. (2022九上·拱墅期中) 如图，四边形ABCD中，对角线AC，BD交于点E. 若 $\text{[math]}$ ，则下列结论中正确的是（）

① $\text{[math]}$
② $\text{[math]}$ 与 $\text{[math]}$ 的周长比为 $\text{[math]}$

③ $\text{[math]}$
④S_△ABE·S_△DCE=S_△ADE·S_△BCE

A . ③④ B . ①②③ C . ①②④ D . ①②③④

答案解析收藏纠错 + 选题
10. (2022九上·义乌期中) 如图，AC，BD是⊙O的两条直径，∠AOD＝60°，点M是劣弧AB上任意一点，过点M作AC的垂线，交AC、BD所在直线于点E、G，过点M作BD的垂线，交BD、AC所在直线于点F、H，小明思考后提出如下说法，其中不正确的是（）

A . $\text{[math]}$ B . ∠EMF＝60° C . 当M平分弧AB时，四边形AMBO为菱形 D . 当△MFG≌△BCD时， $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2023·岱岳模拟) 如图，抛物线 $\text{[math]}$ 与x轴正半轴交于 $\text{[math]}$ 两点，y轴负半轴交于点C.若点 $\text{[math]}$ ，则下列结论中： $\text{[math]}$ $\text{[math]}$ ； $\text{[math]}$ $\text{[math]}$ ； $\text{[math]}$ $\text{[math]}$ 与 $\text{[math]}$ 是抛物线上两点，若 $\text{[math]}$ ，则 $\text{[math]}$ ； $\text{[math]}$ 若抛物线的对称轴是直线 $\text{[math]}$ ， m为任意实数，则 $\text{[math]}$ ； $\text{[math]}$ 若 $\text{[math]}$ 则 $\text{[math]}$ 其中正确结论的个数共有个.

答案解析收藏纠错 + 选题
12. (2023九上·宁波期末) 已知过点 $\text{[math]}$ 的抛物线 $\text{[math]}$ 与坐标轴交于点 $\text{[math]}$ 、 $\text{[math]}$ 如图所示，连结 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，第一象限内有一动点 $\text{[math]}$ 在抛物线上运动，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，当点 $\text{[math]}$ 在点 $\text{[math]}$ 上方，且 $\text{[math]}$ 与 $\text{[math]}$ 相似时，点 $\text{[math]}$ 的坐标为.

答案解析收藏纠错 + 选题
13. (2022九上·长兴月考) 如图，函数y=ax²+bx+c(a，b，c为常数，且a≠0)经过点(-1，0)，(m，0)，且1<m<2，下列结论：①abc>0；②a+b<0；③若点A(-2，y₁)，B(2，y₂)在抛物线上，则y₁< y₂；④
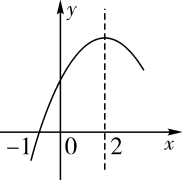
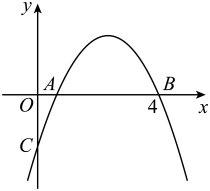
若1≤c≤2，则a的取值范围是-2<a< $\text{[math]}$ ．其中结论正确的有．(填序号)

答案解析收藏纠错 + 选题
14. (2022九上·成都月考) 已知，如图所示，矩形 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 边上的一动点.连接 $\text{[math]}$ ，过 $\text{[math]}$ 作 $\text{[math]}$ 垂足为 $\text{[math]}$ 点，交 $\text{[math]}$ 于 $\text{[math]}$ 点.过A作 $\text{[math]}$ ，垂足为 $\text{[math]}$ ，连接 $\text{[math]}$ .则四边形 $\text{[math]}$ 面积的最大值为.

答案解析收藏纠错 + 选题
15. (2022九上·舟山期中) 已知关于 $\text{[math]}$ 的二次函数 $\text{[math]}$ ，其中 $\text{[math]}$ 为实数，当-2≤x≤1时， $\text{[math]}$ 的最小值为4，满足条件的 $\text{[math]}$ 的值为。

答案解析收藏纠错 + 选题
16. (2023九上·兰溪月考) 如图，正五边形 $\text{[math]}$ 的对角线 $\text{[math]}$ 和 $\text{[math]}$ 分别交对角线 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ 的面积为 $\text{[math]}$ ，则正五边形 $\text{[math]}$ 的面积为（结果用含 $\text{[math]}$ 的代数式表示）.

答案解析收藏纠错 + 选题
17. (2023九上·宿城期末) 在平面直角坐标系中，已知点 $\text{[math]}$ ，点 $\text{[math]}$ ，点 $\text{[math]}$ ，动点D从A点出发，以每秒1个单位的速度水平向右运动，动点E从点B出发，以每秒1个单位的速度竖直向上运动，过点A作 $\text{[math]}$ 交 $\text{[math]}$ 于点G，当线段 $\text{[math]}$ 的值最小时，则运动时间t的值为 .

答案解析收藏纠错 + 选题
18. (2023九上·余姚期末) 定义：有一个圆分别和一个三角形的三条边各有两个交点，截得的三条弦相等，我们把这个圆叫作“等弦圆”，现在有一个斜边长为6的等腰直角三角形，当等弦圆最大时，这个圆的半径为 .

答案解析收藏纠错 + 选题

三、解答题

19. (2019九上·海淀期中) 生活中看似平常的隧道设计也很精巧．如图是一张盾构隧道断面结构图，隧道内部为以O为圆心AB为直径的圆．隧道内部共分为三层，上层为排烟道，中间为行车隧道，下层为服务层．点A到顶棚的距离为0.8a，顶棚到路面的距离是3.2a，点B到路面的距离为2a．请你求出路面的宽度l．（用含a的式子表示）

答案解析收藏纠错 + 选题

20. (2022九上·温州月考) 根据以下素材，探索完成任务．

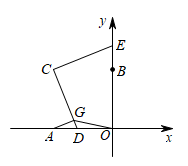
如何设计喷灌器喷水口的升降方案
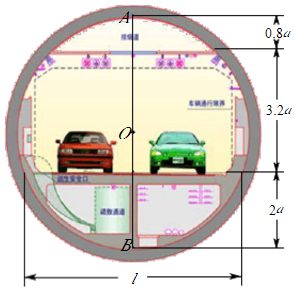
素材1	随着自动化设备的普及，家庭庭院也引入自动喷灌系统．图1中某庭院内有一个可垂直升降的草坪喷灌器，从喷水口喷出的水柱成抛物线形．图2是该喷灌器OA喷水时的截面示意图，喷水口A点离地高度为0.25m，喷出的水柱在离喷水口水平距离为2m处达到最高，高度为0.45m，且水柱刚好落在庭院围墙和地面的交界B点处．
素材2	为了美化庭院，准备在庭院内沿围墙建花坛种植绣球花，花坛高0.4m，宽0.8m，侧面用大理石包围，长方形BCDE是花坛截面，如图3．调整喷水口的高度，喷出的水柱形状与原来相同，水柱落在花坛的上方DE边上（大理石厚度不计），达到给花坛喷灌的效果．
问题解决
任务1	确定水柱的形状	在图2中，建立合适的平面直角坐标系，求抛物线的表达式．
任务2	确定喷灌器的位置	求出喷灌器OA与围墙的距．
任务3	拟定喷头升降方案	调整喷水口的高度，使水柱可以喷灌花坛，求喷水口距离地面高度的最小值．

答案解析收藏纠错 + 选题

21. (2021九上·玉屏期末) 如图，已知：关于y的二次函数 $\text{[math]}$ 的图象与x轴交于点 $\text{[math]}$ 和点B，与y轴交于点 $\text{[math]}$ ，抛物线的对称轴与x轴交于点D.
1. （1）求二次函数的表达式.
2. （2）在y轴上是否存在一点P，使 $\text{[math]}$ 为直角三角形.若存在，请求出点P的坐标.
3. （3）有一个点M从点A出发，以每秒1个单位的速度在 $\text{[math]}$ 上向点B运动，另一个点N从点D与点M同时出发，以每秒2个单位的速度在抛物线的对称轴上运动，当点M到达B点时，点M、N同时停止运动，问点M、N运动到何处时， $\text{[math]}$ 面积最大，试求出面积.
答案解析收藏纠错 + 选题
22. (2020九上·红桥期末) 已知⊙O的直径为10，点A ，点B ，点C在⊙O上，∠CAB的平分线交⊙O于点D ．

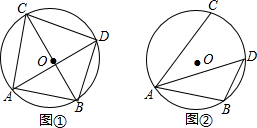
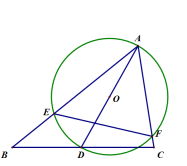
（Ⅰ）如图①，若BC为⊙O的直径，AB＝6，求AC ， BD ， CD的长；

（Ⅱ）如图②，若∠CAB＝60°，求BD的长．

答案解析收藏纠错 + 选题
23. (2020九上·梅河口期末) 如图是一纸杯，它的母线AC和EF延长后形成的立体图形是圆锥，该圆锥的侧面展开图形是扇形OAB．经测量，纸杯上开口圆的直径是6cm，下底面直径为4cm，母线长为EF=8cm．求扇形OAB的圆心角及这个纸杯的表面积（面积计算结果用表示）．

答案解析收藏纠错 + 选题
24. (2019九上·南关期末) 如图，在Rt△ABC中，∠ACB＝90°，AC＝16，BC＝12，点D、E分别为边AB、BC中点，点P从点A出发，沿射线AB方向以每秒5个单位长度的速度向点B运动，到点B停止．当点P不与点A重合时，过点P作PQ∥AC ，且点Q在直线AB左侧，AP＝PQ ，过点Q作QM⊥AB交射线AB于点M ．设点P运动的时间为t（秒）
1. （1）用含t的代数式表示线段DM的长度；
2. （2）求当点Q落在BC边上时t的值；
3. （3）设△PQM与△DEB重叠部分图形的面积为S（平方单位），当△PQM与△DEB有重叠且重叠部分图形是三角形时，求S与t的函数关系式；
4. （4）当经过点C和△PQM中一个顶点的直线平分△PQM的内角时，直接写出此时t的值．
答案解析收藏纠错 + 选题