已知:如图, ,
,
. 求证:
平分
.

证明:∵ ,
,
∴ ,
. ( )(填推理依据)
∴ .
∴ . ( )(填推理依据)
∴ . ( )(填推理依据)
. ( )(填推理依据)
又∵ , ∴
.
∴平分
. ( )(填推理依据)
请完成下面的证明及理由填写.

证明:∵(已知),
∴(垂直的定义),
∵(已知),
∴( ),
∴(等量代换)
∴( ).
∴( )
又∵(已知),
∴ ▲ ( )
∴( )
∴( )
已知:如图,点在直线
上,点
在直线
上,
,
. 求证:
.

证明:∵(已知)
( )
∴(等量代换)
∴( )
∴ ▲
(两直线平行,同旁内角互补)
又∵(已知)
∴ ▲ (等量代换)
∴ ▲ ▲ ( )
∴( )
如图,于
,
于
,
, 可得
平分
.

理由如下:于
,
于
, (已知)
, (垂直的定义)
, ( )
▲ , ( )
, ( )
又 , (已知)
▲ , (等量代换)
平分
(角平分线的定义)
已知:如图, ,
.
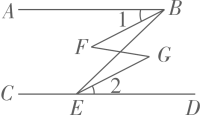
求证:.
证明:∵(已知),
∴ ▲ // ▲ ( ).
∴( ).
又∵(已知),
∴( ).
即.
∴ ▲ // ▲ ( ).
∴(两直线平行,内错角相等).

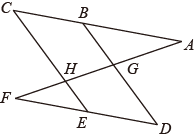





①求∠AEC的大小(用含α,β的代数式表示);
②作∠ECD的平分线交AB于点G,连接GE,AG平分于∠CGE(如图3).若∠AEG=130°,α+β=80°,分别求出α,β的度数.
②如图4,已知 , 点
,
分别在射线
,
上,在
与
内部作射线
,
, 使
平行于
, 请直接写出
与
之间的数量关系.
①当 ,
时,求
的度数;
②小安将三角板沿直线
左右移动,保持
, 点
、
分别在直线
和直线
上移动,请直接写出
的度数(用含
的式子表示).