2023年浙教版数学八年级上册2.8 直角三角形全等的判定 ...

更新时间：2023-08-07 浏览次数：55 类型：同步测试

一、选择题（每题3分，共30分）

1. (2021八上·福绵期末) 如图，已知 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020八上·石屏期末) 如图，点P到 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的距离恰好相等，则点P的位置：①在 $\text{[math]}$ 的平分线上；②在 $\text{[math]}$ 的平分线上；③在 $\text{[math]}$ 的平分线上；④恰好是 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三条平分线的交点．上述结论中，正确的个数有（）

A . $\text{[math]}$ 个 B . $\text{[math]}$ 个 C . $\text{[math]}$ 个 D . $\text{[math]}$ 个

答案解析收藏纠错 + 选题
3. (2022八上·汾阳期末) 如图，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别是 $\text{[math]}$ ， $\text{[math]}$ 上的动点，当 $\text{[math]}$ 取得最小值时， $\text{[math]}$ 的长是（）

A . 8 B . 10 C . 12 D . 16

答案解析收藏纠错 + 选题
4. (2021八上·奉化期末) 如图，在等腰△ $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，O是△ $\text{[math]}$ 外一点，O到三边的垂线段分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ 的长度为（）

A . 5 B . 6 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2021八上·宁波期中) 如图，∠ABC＝40°，BD平分∠ABC，过D作DE∥AB交BC于点E，若点F在AB上，且满足DF＝DE，则∠DFB的度数为（　　）

A . 20° B . 140° C . 40°或140° D . 20°或140°

答案解析收藏纠错 + 选题
6. (2021八上·南通月考) 如图， $\text{[math]}$ 的外角 $\text{[math]}$ ， $\text{[math]}$ 的平分线 $\text{[math]}$ ， $\text{[math]}$ 相交于点P， $\text{[math]}$ 于E， $\text{[math]}$ 于F，下列结论：（1） $\text{[math]}$ ；（2）点P在 $\text{[math]}$ 的平分线上；（3） $\text{[math]}$ ；（4）若 $\text{[math]}$ ，则 $\text{[math]}$ ，其中正确的有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
7. (2021八上·孝感期末) 如图， $\text{[math]}$ 中， $\text{[math]}$ 的平分线 $\text{[math]}$ 与边 $\text{[math]}$ 的垂直平分线 $\text{[math]}$ 相交于 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于 $\text{[math]}$ 于F，现有下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ 平分 $\text{[math]}$ ；④若 $\text{[math]}$ ，则 $\text{[math]}$ .其中正确的个数为（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
8. (2021八上·汇川期末) 如图 $\text{[math]}$ 是 $\text{[math]}$ 的角平分线， $\text{[math]}$ 于E，点F，G分别是 $\text{[math]}$ ， $\text{[math]}$ 上的点，且 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 的面积分别是10和3，则 $\text{[math]}$ 的面积是（）

A . 4 B . 5 C . 6 D . 7

答案解析收藏纠错 + 选题
9. (2023八下·龙岗期中) 如图，点P为定角∠AOB平分线上的一个定点，且∠MPN与∠AOB互补.若∠MPN在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：①PM=PN；②OM+ON的值不变；③MN的长不变；④四边形PMON的面积不变，其中，正确结论的是（）

A . ①②③ B . ①②④ C . ①③④ D . ②③④

答案解析收藏纠错 + 选题
10. (2019八上·赛罕期中) 如图所示， $\text{[math]}$ 是 $\text{[math]}$ 的角平分线， $\text{[math]}$ ，垂足为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 和 $\text{[math]}$ 的面积分别为49，40，则 $\text{[math]}$ 的面积为（）

A . 3.5 B . 4.5 C . 9 D . 10

答案解析收藏纠错 + 选题

二、填空题（每空4分，共24分）

11. (2021八上·彭州开学考) 如图所示，在等腰△ABC中，AB＝AC，∠B＝50°，D为BC的中点，点E在AB上，∠AED＝73°，若点P是等腰△ABC的腰上的一点，则当△EDP为以DE为腰的等腰三角形时，∠EDP的度数是.

答案解析收藏纠错 + 选题
12. (2023八上·团风期中) 如图，AP，BP分别平分△ABC内角∠CAB和外角∠CBD，连接CP，若∠ACP＝130°，则∠APB＝．

答案解析收藏纠错 + 选题
13. (2021八上·余杭月考) 如图， $\text{[math]}$ ABC中，∠ABC、∠EAC的角平分线BP、AP交于点P，延长BA、BC，PM⊥BE，PN⊥BF，则下列结论中正确的是.
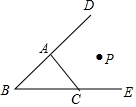
①CP平分∠ACF；②∠ABC＋2∠APC＝180°；③∠ACB＝2∠APB；④S_△PAC＝S_△MAP＋S_△NCP.

答案解析收藏纠错 + 选题
14. (2023七下·莲湖月考) 如图，已知等边 $\text{[math]}$ 和等边 $\text{[math]}$ ，点P在BC的延长线上，EC的延长线交AP于点M，连接BM；下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③BM平分 $\text{[math]}$ ；④ $\text{[math]}$ ，其中正确的有（填序号）．

答案解析收藏纠错 + 选题
15. (2021八上·苏州月考) 如图，任意画一个∠BAC=60°的△ABC，再分别作△ABC的两条角平分线BE和CD，BE和CD相交于点P，连接AP，有以下结论：①∠BPC=120°；②AP平分∠BAC；③AD=AE；④PD=PE；⑤BD+CE=BC；其中正确的结论为．（填写序号）

答案解析收藏纠错 + 选题
16. (2022八上·台州月考) 如图，在 $\text{[math]}$ ABC中，AH是高，AE $\text{[math]}$ BC，AB＝AE，在AB边上取点D，连接DE，DE＝AC，若 $\text{[math]}$ ，BH＝1，则BC＝.

答案解析收藏纠错 + 选题

三、综合题（共8题，共66分）

17. (2022八上·宁波期末) 定义：如果三角形的两个内角 $\text{[math]}$ 和 $\text{[math]}$ 满足 $\text{[math]}$ ，那么我们称这样的三角形为“类直角三角形”.如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .请把这个三角形分割成两个三角形，使得其中一个为“类直角三角形”，并求出这个“类直角三角形”的面积.（备注：要求尺规作图）

答案解析收藏纠错 + 选题
18. (2021八上·江汉期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 是角平分线， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 在边AC上， $\text{[math]}$ .
1. （1）如图1，若 $\text{[math]}$ ，求证： $\text{[math]}$ ；
2. （2）如图2，求证： $\text{[math]}$ ；
3. （3）若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，直接写出 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
19. (2021八上·宁波期中) 已知在△ABC中，∠CAB的平分线AD与BC的垂直平分线DE交于点D，DM⊥AB于M，DN⊥AC的延长线于N.
1. （1）证明：BM＝CN.
2. （2）当∠BAC＝70°时，求∠DCB的度数；
3. （3）若AB＝8，AC＝4，DE＝3，则4DN²﹣BC²的值为 .
答案解析收藏纠错 + 选题
20. (2022七下·张家港期末) 如图，∠MAN是一个钝角，AB平分∠MAN，点C在射线AN上，且AB＝BC，BD⊥AC，垂足为D．
1. （1）求证： $\text{[math]}$ ；
2. （2）动点P，Q同时从A点出发，其中点Q以每秒3个单位长度的速度沿射线AN方向匀速运动；动点P以每秒1个单位长度的速度匀速运动．已知AC＝5，设动点P，Q的运动时间为t秒．
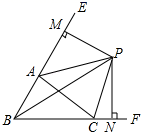
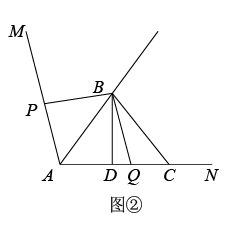
  ①如图②，当点P在射线AM上运动时，若点Q在线段AC上，且 $\text{[math]}$ ，求此时t的值；
  ②如图③，当点P在直线AM上运动时，点Q在射线AN上运动的过程中，是否存在某个时刻，使得 $\text{[math]}$ APB与 $\text{[math]}$ BQC全等？若存在，请求出t的值；若不存在，请说出理由．
答案解析收藏纠错 + 选题
21. (2022七下·香坊期末) △ABC中，∠ACB＝90°，AC＝BC ，点D是射线BC上一点，连接AD ，过点B作BF⊥AD于点F ，直线BF、AC交于点E ．
1. （1）如图1，当点D在线段BC的延长线上时，求证：AC＋CE＝BD；
2. （2）如图2，当点D在线段BC上时，求证：FC平分∠AFE；
3. （3）如图3，在（2）的条件下，若点D是BC的中点，△AFE的面积为36，求AF的长．
答案解析收藏纠错 + 选题
22. (2021八上·抚顺期末) 如图①，C、F分别为线段AD上的两个动点，BC⊥AD，垂足为C，EF⊥AD，垂足为F，且AB==DE，AF=CD，点G是AD与BE 的交点.
1. （1）求证∶ BG=EG；
2. （2）当C、F两点移动到如图②的位置时，其余条件不变，上述结论能否成立?若成立，请给予证明；若不成立，请说明理由.
答案解析收藏纠错 + 选题
23. (2022七下·海陵期末) 如图，∠MON=90°，点A、B分别在射线OM、ON上，点C在∠MON内部．
1. （1）若OA=OB，
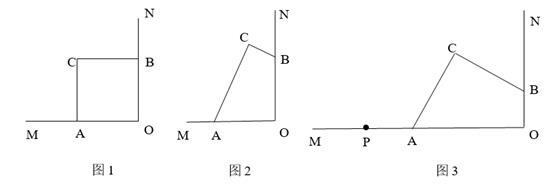
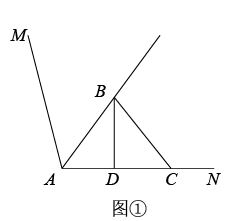
  ①如图1，若CA⊥OM，CB⊥ON．求证：CA=CB．
  
  ②如图2，若∠ACB=90°．求证：OC平分∠ACB．
2. （2）如图3，点A、B分别在射线OM、ON上运动，点C随之运动，且∠ACB=90°，AC=BC．P为OM上一定点，当点C运动到何处时，PC的长度最短？
  请用尺规作图作出PC最短时C点的位置（保留作图痕迹，不要写作法），并请简要说明理由．
答案解析收藏纠错 + 选题
24. (2021七下·松北期末) 在 $\text{[math]}$ 中， $\text{[math]}$ .
1. （1）如图1、求证： $\text{[math]}$ ：
2. （2）如图2，D为AB上一点，连接CD，E为CD中点，过点E作 $\text{[math]}$ 于点E，连接 $\text{[math]}$ ，求证： $\text{[math]}$ ；
3. （3）如图3，在（2）的条件下，过点F作 $\text{[math]}$ 于点H，连接AF，若 AF∥BC，FH=4，CH=20，BD=10 ，求 $\text{[math]}$ 的面积
答案解析收藏纠错 + 选题