备考2024年浙江中考数学一轮复习专题21.1四边形基础夯...

更新时间：2024-03-02 浏览次数：46 类型：一轮复习

一、选择题（每题3分，共30分）

1. (2024九上·盐田开学考) 过某个多边形的一个顶点的所有对角线，将这个多边形分成7个三角形，则这个多边形是（　　）

A . 六边形 B . 七边形 C . 八边形 D . 九边形

答案解析收藏纠错 + 选题
2. (2024七下·沈丘月考) 下列几种形状的瓷砖中，只用一种不能够铺满地面的是（　　）

A . 正六边形 B . 正五边形 C . 正方形 D . 正三角形

答案解析收藏纠错 + 选题
3. (2023九上·西安开学考) 下列说法中的错误的是（　　）

A . 一组邻边相等的矩形是正方形 B . 一组邻边相等的平行四边形是菱形 C . 一组对边相等且有一个角是直角的四边形是矩形 D . 一组对边平行且相等的四边形是平行四边形

答案解析收藏纠错 + 选题
4. (2023九上·瑞安开学考) 在菱形ABCD中，∠B＝60°，用六条线段（虚线表示）把菱形分割成四部分，如图所示，其中PM∥EF∥BC ， PF∥MN∥CD ， FG∥MH∥AC ，且点P在对角线AC上，若求该六条割线长（虚线部分）的和，只需知道（）

A . 六边形PMHCGF的周长 B . 梯形EFGB的周长 C . 梯形MNDH的周长 D . 菱形ABCD的周长

答案解析收藏纠错 + 选题
5. (2023九上·海曙期中) 如图，在正方形 $\text{[math]}$ 中， $\text{[math]}$ 为线段 $\text{[math]}$ 上一点且 $\text{[math]}$ ，连结 $\text{[math]}$ ， $\text{[math]}$ 交于点 $\text{[math]}$ ，分别作 $\text{[math]}$ ， $\text{[math]}$ 的中点M ， N ，连结 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 为（）

A . 1 B . $\text{[math]}$ C . 2 D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023八上·安吉期中) 如图是一张长方形纸片ABCD，点M是对角线AC的中点，点E在BC边上，把△DCE沿直线DE折叠，使点C落在对角线AC上的点F处，连接DF、EF，若MF=CD，则∠DAF的度数为（）

A . 15° B . 16° C . 18° D . 20°

答案解析收藏纠错 + 选题
7. (2023七上·杭州月考) 如图一标志性建筑的底面呈正方形，底面采用4块完全相同的长方形地砖和一块正方形地砖拼成，则以下说法正确的是 $\text{[math]}$ $\text{[math]}$

A . 由长方形地砖的周长可求外面大正方形的面积 B . 由长方形地砖的面积可求外面大正方形的面积 C . 由里面小正方形地砖的周长可求长方形的面积 D . 由里面小正方形地砖的面积可求大正方形的面积

答案解析收藏纠错 + 选题
8. (2023八下·上虞期末) 如图，在菱形 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 为对称中心，点 $\text{[math]}$ 从点 $\text{[math]}$ 出发沿 $\text{[math]}$ 向点 $\text{[math]}$ 移动，移动到点 $\text{[math]}$ 停止，连接 $\text{[math]}$ 并延长交边 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ．则四边形 $\text{[math]}$ 形状的变化依次为（）

A . 平行四边形→矩形→正方形→菱形 B . 平行四边形→矩形→平行四边形→菱形 C . 平行四边形→正方形→菱形→矩形 D . 平行四边形→菱形→平行四边形→菱形

答案解析收藏纠错 + 选题
9. (2023八下·杭州月考) 如图，一块长方形场地ABCD的长AB与宽AD的比为 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ，连接BE，DF，则四边形DEBF与长方形ABCD的面积比为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2021八下·余姚期末) 如图，正方形ABCD中，AC ， E为线段BO上一动点（不包括O ， B两点），DF⊥CE于点F ，过点A作AG⊥DF于点G，交BD于点H ，连结AE ，则下列结论：①∠ADG＝∠DCF；②DG＝EF ， ③存在点E，使得EF＝GF；④四边形AECH是菱形．其中正确的结论有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题（每题3分，共18分

11. (2023九上·温州月考) 若一个正多边形的每个内角为 $\text{[math]}$ ，则这个正多边形的边数是．

答案解析收藏纠错 + 选题
12. (2023九上·市南区期中) 如图，矩形ABCD的对角线AC，BD交于点O，AB=6，BC=8，过点O作OE⊥AC，交AD于点E，过点E作EF⊥BD，垂足为F，则OE+EF的值为.

答案解析收藏纠错 + 选题
13. (2023八下·拱墅期中) 如图，已知 $\text{[math]}$ 的面积为 $\text{[math]}$ ，点 $\text{[math]}$ 在线段 $\text{[math]}$ 上，点 $\text{[math]}$ 在线段 $\text{[math]}$ 的延长线上，且 $\text{[math]}$ ，四边形 $\text{[math]}$ 是平行四边形，则图中阴影部分的面积是．

答案解析收藏纠错 + 选题
14. (2023八下·金东期末) 如图，在菱形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ，将菱形ABCD沿菱形ABCD某一边平移a长度，得菱形 $\text{[math]}$ ；将菱形 $\text{[math]}$ 沿菱形 $\text{[math]}$ 某一边平移a长度，得菱形 $\text{[math]}$ ；将菱形 $\text{[math]}$ 沿菱形 $\text{[math]}$ 某一边平移a长度，得菱形 $\text{[math]}$ ；若四个菱形构成的整个图形为中心对称图形，且四个菱形重叠部分面积为 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2023九上·龙湾开学考) 如图 $\text{[math]}$ 是七巧板图案，现将它剪拼成一个“台灯”造型 $\text{[math]}$ 如图 $\text{[math]}$ ，过该造型的上下左侧五点作矩形 $\text{[math]}$ ，使得 $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 的中点，并且在矩形内右上角部分留出正方形 $\text{[math]}$ 作为印章区域 $\text{[math]}$ ，形成一幅装饰画，则矩形 $\text{[math]}$ 的周长为 $\text{[math]}$ 若点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在同一直线上，且点 $\text{[math]}$ 到 $\text{[math]}$ 的距离与到 $\text{[math]}$ 的距离相等，则印章区域的边长为 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2022·鹿城会考) 郑在一次拼图游戏中，发现了一个很神奇的现象：
⑴他先用图形①②③④拼出矩形ABCD.
⑵接着拿出图形⑤ .
⑶通过平移的方法，用①②③④⑤拼出了矩形ABMN.已知AE：EO = 2：3，图形④的面积为15，则增加的图形⑤的面积为：，当CO= $\text{[math]}$ ， EH=4时，tan∠BAO=.

答案解析收藏纠错 + 选题

三、解答题（共7题，共52分）

17. (2023八下·新昌期末) 在学习多边形的相关知识时，小张同学和小王同学对老师布置“探究多边形的对角线条数”的作业很感兴趣，小张同学探究得到了 $\text{[math]}$ 边形的对角线条数的公式，并通过上网查证自己探究的结论是正确的．下图是两位同学进行交流的情景．小王同学把哪个多边形对角线的条数数错了？请你通过计算或者画图来说明．

答案解析收藏纠错 + 选题
18. (2023八下·温州期末) 如图，在平行四边形 $\text{[math]}$ 中，延长 $\text{[math]}$ 至点F，延长 $\text{[math]}$ 至点E，且 $\text{[math]}$ ．求证：平行四边形 $\text{[math]}$ 是矩形．

答案解析收藏纠错 + 选题
19. (2023九上·杭州开学考) 如图，在▱ABCD中，O为线段AD的中点，延长BO交CD的延长线于点E ，连接AE ， BD ， ∠BDC＝90°．
1. （1）求证：四边形ABDE是矩形；
2. （2）连接OC ，若AB＝2， $\text{[math]}$ ，求OC的长．
答案解析收藏纠错 + 选题
20. (2023八下·东阳期末) 如图1，四边形ABCD为正方形，点A在y轴上，点B在x轴上，且OA＝2OB，反比例函数 $\text{[math]}$ 在第一象限的图象经过正方形的顶点C．
1. （1）求点C的坐标；
2. （2）如图2，将正方形ABCD沿x轴向右平移得到正方形 A'B'CD'，点 A'恰好落在反比例函数的图象上，求此时点 D'的坐标；
3. （3）在（2）的条件下，点P为y轴上一动点，平面内是否存在点Q，使以点O、A'、P、Q为顶点的四边形为菱形，若存在，请直接写出点Q的坐标，若不存在，请说明理由．
答案解析收藏纠错 + 选题
21. (2023八下·海曙期中) 如图1，P是线段AB上的一点，在AB的同侧作△APC和△BPD，使PC=PA，PD=PB，∠APC=∠BPD，连接CD，点E、F、G、H分别是AC、AB、BD、CD的中点，顺次连接E、F、G、H．
1. （1）猜想四边形EFGH的形状是.（直接回答，不必说明理由）
2. （2）当点P在线段AB的上方时，如图2，在△APB的外部作△APC和△BPD，其他条件不变，（1）中的结论还成立吗？说明理由；
3. （3）如果（2）中，∠APC=∠BPD=90°，其他条件不变，先在图3中补全图形，再判断四边形EFGH的形状，并说明理由．
答案解析收藏纠错 + 选题
22. (2023八下·台州期末) 如图1，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点E，F分别在 $\text{[math]}$ ， $\text{[math]}$ 上，将矩形 $\text{[math]}$ 沿直线 $\text{[math]}$ 折叠，使点B落在 $\text{[math]}$ 边上的 $\text{[math]}$ 处，点A落在 $\text{[math]}$ 处，连接 $\text{[math]}$ ．
1. （1）如图2，若点 $\text{[math]}$ 与点D重合，连接 $\text{[math]}$ ．
  
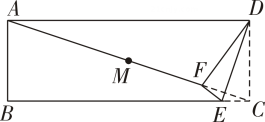
  ①请你判断四边形 $\text{[math]}$ 的形状，并证明；
  ②求 $\text{[math]}$ 的长；
2. （2）如图3，P为 $\text{[math]}$ 中点，连接 $\text{[math]}$ ．
  
  ①当 $\text{[math]}$ 时，求 $\text{[math]}$ 的长；
  
  ②直接写出 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
23. (2023·永康模拟) 如图1，在矩形ABCD中，AB=6，BC=6 $\text{[math]}$ .对角线AC， BD相交于点O，点E， F分别在对角线AC，BD.上，CE=2AE，连结EF.
1. （1）求线段OE的长和∠AOB的度数.
2. （2）当点F在点B处时，以EF为边在右下方作等边△EFG，连结OG.在点F运动过程中，点G也随之运动.如图2，过点F作AB的平行线交AC于点H.若设线段BF长为x，线段OG长为y，求y关于x的函数关系式，并写出相应x的取值范围.
3. （3）若点F在直线BD上运动，以EF为边作等边△EFG.当点G恰好落在矩形ABCD的边上时，求FG的长.
答案解析收藏纠错 + 选题

四、实践探究题（共2题，共20分）

24. (2022八下·衢州期中) 【发现与证明】
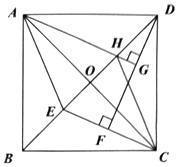
如图，在四边形ABCD中，E、F、G、H是各边中点，对角线AC、BD相交于点O，I、J是AC、BD的中点，连接EF、EH、HG、GF、EI、GI、EJ、FJ、IJ、GJ、IH.
结论1：四边形EFGH是平行四边形；
结论2：四边形EJGI是平行四边形；
结论3： $\text{[math]}$ ；
……
1. （1）请选择其中一个结论，加以证明（只需证明一个结论）.
2. （2）【探究与应用】（★温馨提示：以下问题可以直接使用上述结论）
  ①如图1，在四边形ABCD中，F、H分别为边AB，DC的中点，连结HF.已知 $\text{[math]}$ ， $\text{[math]}$ ，线段HF的取值范围是 ▲ .
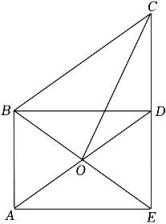
  ②如图2，在四边形ABCD中，点E，F，G，H分别是AB，BC，CD，DA的中点，连接EG，FH交于点O， $\text{[math]}$ cm， $\text{[math]}$ cm， $\text{[math]}$ ，求 $\text{[math]}$ .
答案解析收藏纠错 + 选题
25. (2022九上·温州开学考) 菱形 $\text{[math]}$ 的边长为 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 是对角线 $\text{[math]}$ 中点， $\text{[math]}$ 是线段 $\text{[math]}$ 上任一点，连接 $\text{[math]}$ ，作 $\text{[math]}$ ，边 $\text{[math]}$ 与直线 $\text{[math]}$ 相交于点 $\text{[math]}$ ．

小南和小浦观察以上问题时，猜想 $\text{[math]}$ ，老师引导他们用“从特殊到一般”的思想方法去尝试研究．
1. （1）【特例发现】
  小南发现：当点 $\text{[math]}$ 与点重合时， $\text{[math]}$ 与 $\text{[math]}$ 的长度相等，为；
2. （2）【探究证明】
  小浦认为当 $\text{[math]}$ 在线段 $\text{[math]}$ 上时，均有“ $\text{[math]}$ ”，请帮助完成证明．
3. （3）【拓展运用】
  ①连结 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，求证： $\text{[math]}$ 为定值．
  ②当 $\text{[math]}$ 时， $\text{[math]}$ ▲ ．
答案解析收藏纠错 + 选题