 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
B .
B . 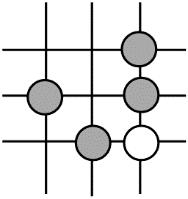
C .
C . 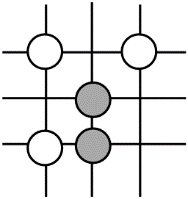
D .
D . 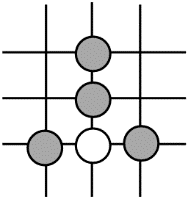





①当时,点
恰好落在反比例函数
图象上,求
的值;
②问点能否同时落在(1)中的反比例函数的图象上?若能,直接写出
的值;若不能,请说明理由.
①当抛物线y1经过点(﹣2,﹣1)时,求a+b+c的值;
②设抛物线y1与x轴的两个交点为A,B(点A在点B的左侧),抛物线y2与x轴的交点为C(在其对称轴左侧).若这三点依次排列后,点B恰好是A,C两点连线的中点,求此时m的值.

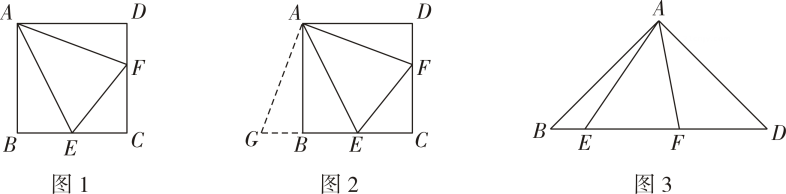
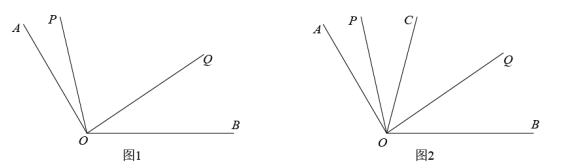
①求的度数;
②设 , 请用
的代数式表示
.