备考2024年中考数学核心素养专题一数学思想方法

更新时间：2024-03-04 浏览次数：239 类型：二轮复习

一、选择题

1. (2023七上·盂县期中) 数轴是我们学习和研究有理数的重要工具，所有的有理数都可以用数轴上的点来表示，体现的数学思想是（）

A . 整体 B . 转化 C . 分类讨论 D . 数形结合

答案解析收藏纠错 + 选题
2. (2022八上·运城月考) 已知直角三角形两边的长分别是3和4，求第三边的长.琪棋的解答过程：“当第三边是斜边时，第三边长为 $\text{[math]}$ .当第三边是直角边时，第三边长为 $\text{[math]}$ .故直角三角形第三边长是5或 $\text{[math]}$ .”琪棋的上述方法体现的数学思想是（）

A . 整体思想 B . 转化思想 C . 数形结合思想 D . 分类讨论思想

答案解析收藏纠错 + 选题
3. (2023七下·交城期中) 如图，以单位长度为边长作正方形，以原点为圆心，正方形的对角线长为半径画弧，与正半轴的交点 $\text{[math]}$ 就表示 $\text{[math]}$ ，与负半轴的交点 $\text{[math]}$ 就表示 $\text{[math]}$ ．这种说明问题的方式体现的数学思想方法叫做（）

A . 分类讨论 B . 数形结合 C . 代入法 D . 换元法

答案解析收藏纠错 + 选题
4. (2024八下·平邑期中) 在学习平行四边形时，我们先学习了平行四边形的性质定理、判定定理，再通过平行四边形边、角的特殊化，获得了特殊的平行四边形——矩形、菱形和正方形，了解了它们之间的关系，并根据它们的特殊性，得到了这些特殊的平行四边形的性质定理和判定定理．在学习这些知识的过程中，主要体现的数学思想是（）

A . 方程思想 B . 数形结合思想 C . 从特殊到一般思想 D . 从一般到特殊思想

答案解析收藏纠错 + 选题
5. (2022·榆次模拟) 公元前3世纪，古希腊数学家欧几里得编写了《几何原本》．他在编写这本书时挑选一部分数学名词和公认的真命题（即公理）作为证实其他命题的出发点和依据，除公理外，其他命题的真假都需要通过演绎推理的方法进行判断，在此基础上，逐渐形成了一种重要的数学思想，这种思想是（）

A . 公理化思想 B . 数形结合思想 C . 分类讨论思想 D . 转化思想

答案解析收藏纠错 + 选题
6. (2022七下·南阳期末) 我们在解二元一次方程组 $\text{[math]}$ 时，可将第二个方程代入第一个方程消去x得﹣2y+y＝6，从而求解，这种解法体现的数学思想是（）

A . 转化思想 B . 分类讨论思想 C . 数形结合思想 D . 函数思想

答案解析收藏纠错 + 选题
7. (2022八上·长顺期中) 为了求n边形内角和，下面是老师与同学们从n边形的个顶点引出的对角线把n边形划分为若干个三角形，然后得出n边形的内角和公式．这种数学的推理方式是（）

A . 归纳推理 B . 数形结合 C . 公理化 D . 演绎推理

答案解析收藏纠错 + 选题
8. (2022·侯马期末) 数学课上，老师在组织同学们探索多边形的内角和公式时，同学们提出了将此问题转化为已学的三角形内角和知识进行探索的思路．如图是四名同学探索多边形内角和公式时运用的不同的分割方法，将多边形转化为多个三角形，并得出了相同的结论．这四名同学在探索过程中主要体现的数学思想是（）

A . 建模思想 B . 分类讨论思想 C . 数形结合思想 D . 转化思想

答案解析收藏纠错 + 选题
9. (2020八上·朔州期末) 代数之父——丢番图(Diophantus)是古希腊的大数学家，是第一位懂得使用符号代表数来研究问题的人．丢番图的墓志铭与众不同，不是记叙文，而是一道数学题．对其墓志铭的解答激发了许多人学习数学的兴趣，其中一段大意为：他的一生幼年占 $\text{[math]}$ ，青少年占 $\text{[math]}$ ，又过了 $\text{[math]}$ 才结婚，5年后生子，子先父4年而卒，寿为其父之半．
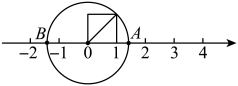
下面是其墓志铭解答的一种方法：

解：设丢番图的寿命为x岁，根据题意得：

$\text{[math]}$ ，

解得 $\text{[math]}$ ．

∴丢番图的寿命为84岁．

这种解答“墓志铭”体现的思想方法是（）

A . 数形结合思想 B . 方程思想 C . 转化思想 D . 类比思想

答案解析收藏纠错 + 选题
10. (2023七上·翠屏月考) 已知点A ， $\text{[math]}$ ， $\text{[math]}$ 在同一条直线上，点 $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ 、 $\text{[math]}$ 的中点，如果 $\text{[math]}$ ， $\text{[math]}$ ，那么线段 $\text{[math]}$ 的长度为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2024七上·嘉祥期末) 若 $\text{[math]}$ ，且m、n异号，则 $\text{[math]}$ 的值为（）

A . 7 B . 3或﹣3 C . 3 D . 7或3

答案解析收藏纠错 + 选题
12. (2023八上·铁锋期末) 如图，在四边形 $\text{[math]}$ 中， $\text{[math]}$ 平分 $\text{[math]}$ 于点 $\text{[math]}$ ，则 $\text{[math]}$ 面积的最大值为（）

A . 2 B . 2.5 C . 4 D . 5

答案解析收藏纠错 + 选题
13. (2023九上·定西月考) 定义一种运算“※”： $\text{[math]}$ （其中x ， y为任意实数）．当 $\text{[math]}$ 时，则 $\text{[math]}$ 的值为（）

A . 7 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

14. (2023七上·翠屏月考) 数轴上A、B两点对应的数分别为 $\text{[math]}$ 和 $\text{[math]}$ ， P为数轴上一点，若 $\text{[math]}$ ，则点P表示的数是．

答案解析收藏纠错 + 选题
15. (2023八上·铁锋期末) 一个等腰三角形两边的长分别为3和8，那么这个等腰三角形的周长是．

答案解析收藏纠错 + 选题
16. (2023七上·偃师期末) “整体思想”是数学中的一种重要的思想方法，它在数学运算、推理中有广泛的应用，如：已知 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ．利用上述思想方法计算：已知 $\text{[math]}$ ， $\text{[math]}$ ．则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
17. (2023九上·运城期中) 如图，在平面直角坐标系中，已知点 $\text{[math]}$ ， $\text{[math]}$ ，以原点 $\text{[math]}$ 为位似中心，相似比为 $\text{[math]}$ ，把 $\text{[math]}$ 缩小，则点 $\text{[math]}$ 的对应点 $\text{[math]}$ 的坐标是．

答案解析收藏纠错 + 选题
18. (2023九上·运城期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 为线段 $\text{[math]}$ 的三等分点，过点 $\text{[math]}$ 作 $\text{[math]}$ ，交射线 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题

三、解答题

19. (2024七上·吉林期末) 下面是小张同学解二元一次方程组的过程，请认真阅读并回答相应的问题．
解方程组： $\text{[math]}$
解： $\text{[math]}$ ，得 $\text{[math]}$ 第一步
$\text{[math]}$ ，得 $\text{[math]}$ 第二步
$\text{[math]}$ 第三步
$\text{[math]}$ 代入 $\text{[math]}$ ，得 $\text{[math]}$ 第四步
所以，原方程组的解为 $\text{[math]}$ 第五步
1. （1）小彬同学的解题过程从第步开始出现错误；
2. （2）请写出正确的解题过程；
3. （3）解二元一次方程组的基本思想是“消元”，即把“二元”变为“一元”，在此过程中体现的数学思想是 $\text{[math]}$ 填序号 $\text{[math]}$ ．
  $\text{[math]}$ .数形结合
  $\text{[math]}$ .类比思想
  $\text{[math]}$ .转化思想
  $\text{[math]}$ .分类讨论
答案解析收藏纠错 + 选题
20. (2023七上·晋城月考) 阅读下列材料，完成后面任务：
计算： $\text{[math]}$ ．
解：原式 $\text{[math]}$ （第一步）
$\text{[math]}$ （第二步）
$\text{[math]}$ （第三步）
$\text{[math]}$ ．（第四步）
任务：
1. （1）材料中运用的数学思想是．（填序号即可）
  ①整体思想；②化归思想；③公理化思想；④数形结合思想．
2. （2）利用材料中的方法计算： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
21. (2023七上·翠屏月考) 如图1，已知∠AOB＝120°，OC是∠AOB内的一条射线，且∠AOC＝ $\text{[math]}$ ∠AOB ， OD平分∠AOC ．
1. （1）分别求∠AOB的补角和∠AOC的度数；
2. （2）现有射线OE ，使得∠BOE＝30°．
  ①小明在图2中补全了射线OE ，根据小明所补的图，求∠DOE的度数；
  ②小静说：“我觉得小明所想的情况并不完整，∠DOE还有其他的结果．”请你判断小静说的是否正确？若正确，请求出∠DOE的其他结果；若不正确，请说明理由．
答案解析收藏纠错 + 选题
22. (2023九上·长沙月考) 在 $\text{[math]}$ 关于 $\text{[math]}$ 的函数中，对于实数 $\text{[math]}$ ，当 $\text{[math]}$ 时，函数 $\text{[math]}$ 的最大值与最小值之差为 $\text{[math]}$ ，且 $\text{[math]}$ 则称此函数为“倍增函数”；
1. （1）当 $\text{[math]}$ ， $\text{[math]}$ 时，判断下列函数是否是“倍增函数”？如果是，请在对应的括号里打“√”，若果不是，请在对应的括号里打“×”
  ① $\text{[math]}$ （ ▲ ），② $\text{[math]}$ （ ▲ ），③ $\text{[math]}$ （ ▲ ）
2. （2）当 $\text{[math]}$ 时，反比例函数 $\text{[math]}$ 为“倍增函数”，求 $\text{[math]}$ 的值；
3. （3）已知二次函数 $\text{[math]}$ 是“倍增函数”，且 $\text{[math]}$ 的最大值为4，求 $\text{[math]}$ 、 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
23. (2023八上·织金期中) 小东家与学校之间是一条笔直的公路，早饭后，小东步行前往学校，途中发现忘带画板，停下给妈妈打电话，妈妈接到电话后，带上画板马上赶往学校，同时小东沿原路返回，两人相遇后，小东立即赶往学校，妈妈沿原路返回，16分钟时到家．假设小东始终以100米/分的速度步行，两人离家的距离 $\text{[math]}$ （单位：米）与小东打完电话后的步行时间（单位：分钟）之间的函数关系如图所示．
1. （1）小东打电话时，他离家米；
2. （2）填上图中空格相应的数据；
3. （3）小东和妈妈相遇后，妈妈回家的速度是多少？
4. （4）求几分钟时两人相距750米．
答案解析收藏纠错 + 选题

24. (2023九上·小店期中) 阅读下列材料，并完成相应的任务.

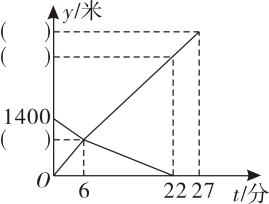
一元二次方程的几何解法

通过学习，我们知道可以用配方法、提公因式法、公式法等求解一元二次方程，但在数学史上人类对一元二次方程的研究经历了漫长的岁月.下面是9世纪阿拉伯数学家阿尔·花拉子米利用几何法求解 $\text{[math]}$ 的过程.

解：如图，构造一个以未知数x为边长的正方形，在某四条边上向外作长和宽分别x和 $\text{[math]}$ 的矩形，再把这个图补成边长为 $\text{[math]}$ 的正方形.

于是大正方形的面积为： $\text{[math]}$ ，

又已知 $\text{[math]}$ ，所以大正方形的面积为 $\text{[math]}$ ，

于是大正方形的边长为8，因此： $\text{[math]}$ .

几何法求解一元二次方程，只能得到正数解.

任务：根据上述材料请你用几何方法求方程 $\text{[math]}$ 的正数解.要求如下：

（1）在如图所示的区域内画出图形，并标出相应的线段长度.
（2）根据（1）所画图形直接写出方程 $\text{[math]}$ 的正数解.
（3）这种构造图形解一元二次方程的方法体现的数学思想是▲ .（填写字母序号即可）
$\text{[math]}$ . 分类讨论思想 $\text{[math]}$ . 数形结合思想 $\text{[math]}$ . 公理化思想

答案解析收藏纠错 + 选题

25. (2024九上·长沙月考) 若函数G在m≤x≤n（m＜n）上的最大值记为y_max ，最小值记为y_min ，且满足y_max﹣y_min＝1，则称函数G是在m≤x≤n上的“最值差函数”．
1. （1）函数① $\text{[math]}$ ；②y＝x+1；③y＝x² ．其中函数是在1≤x≤2上的“最值差函数”；（填序号）
2. （2）已知函数G：y＝ax²﹣4ax+3a（a＞0）．
  ①当a＝1时，函数G是在t≤x≤t+1上的“最值差函数”，求t的值；
  ②函数G是在m+2≤x≤2m+1（m为整数）上的“最值差函数”，且存在整数k ，使得 $\text{[math]}$ ，求a的值．
答案解析收藏纠错 + 选题
26. (2024九上·扶余期末) 自主学习，请阅读下列解题过程．
解一元二次不等式： $\text{[math]}$ ＞0．
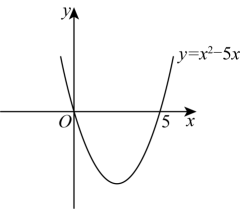
解：设 $\text{[math]}$ =0，解得： $\text{[math]}$ =0， $\text{[math]}$ =5，则抛物线y= $\text{[math]}$ 与x轴的交点坐标为（0，0）和（5，0）．画出二次函数y= $\text{[math]}$ 的大致图象（如图所示），由图象可知：当x＜0，或x＞5时函数图象位于x轴上方，此时y＞0，即 $\text{[math]}$ ＞0，所以，一元二次不等式 $\text{[math]}$ ＞0的解集为：x＜0或x＞5．
通过对上述解题过程的学习，按其解题的思路和方法解答下列问题：
1. （1）上述解题过程中，渗透了下列数学思想中的和．（只填序号）
  ①转化思想 ②分类讨论思想 ③数形结合思想
2. （2）一元二次不等式 $\text{[math]}$ ＜0的解集为．
3. （3）用类似的方法解一元二次不等式： $\text{[math]}$ ＞0．
答案解析收藏纠错 + 选题

四、实践探究题

27. (2023七上·容县期中) 在解决数学问题的过程中，我们常用到“分类讨论“的数学思想，下面是运用“分类讨论”的数学思想解决问题的过程，请仔细阅读，并解答问题．
【提出问题】已知有理数x ， y ， z满足xyz＞0，求 $\text{[math]}$ 的值．
【解决问题】解：由题意，得x ， y ， z三个都为正数或其中一个为正数，另两个为负数．
①当x ， y ， z都为正数，即x＞0，y＞0，z＞0时， $\text{[math]}$ ；
②当x ， y ， z中有一个为正数，另两个为负数时，不妨设x＞0，y＜0，z＜0，则 $\text{[math]}$ ．
综上所述， $\text{[math]}$ 的值为3或-1．
【探究拓展】请根据上面的解题思路解答下面的问题：
1. （1）已知x ， y是不为0的有理数，当|xy|＝-xy时， $\text{[math]}$ ＝；
2. （2）已知x ， y ， z是有理数，当xyz＜0时，求 $\text{[math]}$ 的值；
3. （3）已知x ， y ， z是有理数，x+y+z＝0，xyz＜0，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
28. (2023七上·珠海期中) 阅读理解：整体代换是一种重要的数学思想方法．例如：计算2（2m+n）-5（2m+n）+（2m+n）时，可将（2m+n）看成一个整体，合并同类项得-2（2m+n），再利用分配律去括号得-4m-2n ．
1. （1）若已知2m+n＝3，请你利用整体代换思想求代数式8m+4n-12的值；
2. （2）某同学做一道题，已知两个多项式A、B ，求A-B的值．他误将“A-B”看成“A+B”，经过正确计算得到的结果是2x²+14x-6．已知：A＝x²+7x-1，请你帮助这位同学求出A-B正确的值．
答案解析收藏纠错 + 选题
29. (2023八上·江源月考) [阅读理解]若x满足（32-x）（x-12） = 100，求（32-x）²+ （x-12）²的值。
解；设32-x=a．x-12= b，则（32-x）（x-12）= ab= 100，a+b= （32-x） +（x-12） = 20，（32-x）²+（x-12）²=a²+b²= （a+b）²- 2ab = 20²-2×100=200．
我们把这种方法叫做换元法，利用换元法达到简化方程的目的，体现了转化的数学思想．
[解决问题]
1. （1）若x满足（100-x）（x-95） = 5，则（100-x）²+（x-95）² = ；
2. （2）若x满足（2023-x）² +（x-2000）² = 229 ，求（2023-x）（x-2000）的值；
3. （3）如图，在长方形ABCD中，AB = 24cm，点E、F是边BC、CD上的点，EC= 12cm，且BE = DF = xcm，分别以FC、CB为边在长方形ABCD外侧作正方形CFGH和CBMN，若长方形CBQF的面积为320cm² ，求图中阴影部分的面积和．
答案解析收藏纠错 + 选题

30. 阅读下面方框内的内容，并完成相应的任务.

小丽学习了方程、不等式、函数后提出如下问题：如何求不等式 $\text{[math]}$ 的解集？通过思考，小丽得到以下3种方法：

方法1方程 $\text{[math]}$ 的两根为 $\text{[math]}$ $\text{[math]}$ ，可得函数 $\text{[math]}$ 的图象与 $\text{[math]}$ 轴的两个交点横坐标为 $\text{[math]}$ ，画出函数图象，观察该图象在 $\text{[math]}$ 轴下方的点，其横坐标的范围是不等式 $\text{[math]}$ 的解集.方法2不等式 $\text{[math]}$ 可变形为 $\text{[math]}$ $\text{[math]}$ ，问题转化为研究函数 $\text{[math]}$ 与 $\text{[math]}$ $\text{[math]}$ 的图象关系.画出函数图象，观察发现；两图象的交点横坐标也是 $\text{[math]}$ 的图象在 $\text{[math]}$ 的图象下方的点，其横坐标的范围是该不等式的解集.方法3当 $\text{[math]}$ 时，不等式一定成立；当 $\text{[math]}$ $\text{[math]}$ 时，不等式变为 $\text{[math]}$ ；当 $\text{[math]}$ 时，不等式变为 $\text{[math]}$ .问题转化为研究函数 $\text{[math]}$ 与 $\text{[math]}$ 的图象关系 $\text{[math]}$