备考2024年中考数学探究性训练专题10 不等式（组）

更新时间：2024-03-27 浏览次数：26 类型：二轮复习

一、选择题

1. (2022八下·惠来期中) 某班数学兴趣小组对不等式组 $\text{[math]}$ ，讨论得到以下结论：
①若 $\text{[math]}$ ，则不等式组的解集为 $\text{[math]}$ ；
②若 $\text{[math]}$ ，则不等式组无解；
③若不等式组有解，则a的取值范围 $\text{[math]}$ ；
④若不等式组只有四个整数解，则a的值只可以为7；
其中，正确结论的个数是（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题

2. (2022七下·浉河期末) 在数学著作《算术研究》一书中，对于任意实数，通常用[x]表示不超过x的最大整数，如：[π]＝3，[2]＝2，[﹣2.1]＝﹣3．当﹣1＜x＜1时，[1+x]+[1﹣x]的值为．

答案解析收藏纠错 + 选题
3. (2023七下·内江期中) 某学校九年级的一个研究性学习小组对学生中午在学校食堂的就餐时间进行了调查．发现在单位时间内，每个窗口买走午餐的人数和因不愿长久等待而到小卖部就餐的人数各是一个固定数．并且发现若开1个窗口，45分钟可使等待人都能买到午餐；若同时开2个窗口，则需30分钟．还发现，若在25分钟内等待的学生都能买到午餐，在单位时间内，外出就餐的人数可减少80%．在学校学生总人数不变且人人都要就餐的情况下，为了方便学生就餐，调查小组建议学校食堂20分钟内卖完午餐，则至少要同时开个窗口．

答案解析收藏纠错 + 选题
4. 某班数学兴趣小组对不等式组 $\text{[math]}$ ，进行讨论，得到以下结论：
①若a=5，则不等式组的解为3<x≤5；
②若a=2，则不等式组无解；
③若不等式组无解，则a的取值范围为a<3；
④若不等式组只有两个整数解，则a的值可以为5．
其中，正确结论的序号是.

答案解析收藏纠错 + 选题
5. (2020七下·赣县期末) 某班数学兴趣小组对不等式组 $\text{[math]}$ ，讨论得到以下结论：①若a＝5，则不等式组的解集为3<x≤5；②若a＝2，则不等式组无解；③若不等式组无解，则a的取值范围为a<3；④若不等式组只有两个整数解，则a的值可以为5.1,其中，正确的结论的序号是．

答案解析收藏纠错 + 选题

三、理论探究题

6. (2023七下·二道期末) 下面是张莉同学解不等式的过程，请认真阅读并完成相应任务．
解不等式： $\text{[math]}$ ．
去分母，得24-（x-7）＞8x+4．
1. （1）任务一：“去分母”这一步的变形依据是____（填“A”或“B”）．
  
  A . 不等式两边乘（或除以）同一个正数，不等号的方向不变． B . 不等式两边乘（或除以）同一个负数，不等号的方向改变．
2. （2）任务二：请完成上述解不等式的余下步骤，并把解集表示在数轴上．
答案解析收藏纠错 + 选题
7. (2021八下·邛崃期末) 阅读理解题
问题提出：如果一个正整数能表示为两个正整数的平方差，那么称这个正整数为“幸福数”.例如， $\text{[math]}$ ， 16就是一个幸福数.我们按照从小到大的顺序把“3，5，7，8，…， $\text{[math]}$ ， …” 这些幸福数进行排列依次记为：第1个幸福数3，第2个幸福数5，第3个幸福数7，第4个幸福数8，…，第 $\text{[math]}$ 个幸福数 $\text{[math]}$ .现在需要探究出一种判断一个较大的数是否是幸福数的方法；以及如何求出第 $\text{[math]}$ 个幸福数 $\text{[math]}$ 的值.

实践探究：小明的方法是：在正整数中，从1开始采取从小到大逐个排查的办法一个一个找出来：

$\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，

$\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，

…
1. （1）请将第10个幸福数仿照小明的方法用等式表示出来：；
  小颖认为小明的方法太麻烦，她想到：设 $\text{[math]}$ 是正整数，由于 $\text{[math]}$ ，所以，除1外，所有的奇数都是幸福数；又因为 $\text{[math]}$ 所以，除4外，所有能被4整除的偶数都是幸福数；小颖通过上面的探索，已经证明了形如 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ （ $\text{[math]}$ 是正整数）的正整数都是幸福数.
2. （2）请证明形如 $\text{[math]}$ （ $\text{[math]}$ 是正整数）的数不是幸福数；
3. （3）迁移应用：当 $\text{[math]}$ 时，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
8. (2021七下·高平期末) 阅读下面材料，完成任务．
某数学兴趣小组在一次课外学习与探究中遇到一个新的运算符号，他们将其中某些材料摘录如下：对于三个数 $\text{[math]}$ ，用 $\text{[math]}$ 表示这三个数中最大的数，例如： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，请结合上面材料，解决下列问题：
1. （1） $\text{[math]}$ =
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
9. (2023八上·期中) 我们用[a]表示不大于a的最大整数，例如：[2.5]＝2，[3]＝3，[-2.5]＝-3；用＜a＞表示大于a的最小整数，例如：＜2.5＞＝3，＜3＞＝4，＜-2.5＞＝-2．根据上述规定，解决下列问题：
1. （1） [-4.5]＝，＜3.01＞＝；
2. （2）若x为整数，且[x]+＜x＞＝2023，求x的值；
3. （3）若x、y满足方程组 $\text{[math]}$ ，求x、y的取值范围．
答案解析收藏纠错 + 选题
10. (2023八上·镇海区期中) 在平面直角坐标系中，对于点 $\text{[math]}$ ，若点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，其中 $\text{[math]}$ 为常数，对称点 $\text{[math]}$ 是点 $\text{[math]}$ 的“ $\text{[math]}$ 级关联点”，例如：点 $\text{[math]}$ 的“2级关联点” $\text{[math]}$ ，即 $\text{[math]}$ .
1. （1）已知点 $\text{[math]}$ 的：“3级关联点”为 $\text{[math]}$ ，求点 $\text{[math]}$ 的坐标；
2. （2）已知点 $\text{[math]}$ 关于“2级关联点”为 $\text{[math]}$ ，求 $\text{[math]}$ 的坐标；
3. （3）点 $\text{[math]}$ 关于-4级关联点在第三象限，求 $\text{[math]}$ 的范围。
答案解析收藏纠错 + 选题
11. (2023八下·珠山期中) 阅读材料并完成相应的任务．
小逸在趣味数学书上看到这样一道题：已知 $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ，设 $\text{[math]}$ ，那么 $\text{[math]}$ 的取值范围是什么？

【回顾】

小逸回顾做过的一道简单的类似题目：

已知 $\text{[math]}$ ，设 $\text{[math]}$ ，那么 $\text{[math]}$ 的取值范围是 ① ．

【探究】

小逸想：可以将趣味数学书上的复杂问题转化为上面回顾的类似题目．

由 $\text{[math]}$ 得 $\text{[math]}$ ，则 $\text{[math]}$ ，

由 $\text{[math]}$ ， $\text{[math]}$ ，得关于 $\text{[math]}$ 的一元一次不等式组 ② ，

解该不等式组得到 $\text{[math]}$ 的取值范围为 ③ ，

则 $\text{[math]}$ 的取值范围是 ④ ．
1. （1）任务一：补充材料中的信息．
  ①：；②：；③：；④：．
2. （2）任务二：（ⅰ）已知 $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ，设 $\text{[math]}$ ，求 $\text{[math]}$ 的取值范围．
  （ⅱ）若 $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，设 $\text{[math]}$ ，且 $\text{[math]}$ 为整数，求 $\text{[math]}$ 所有可能的值的和．
答案解析收藏纠错 + 选题
12. (2023八下·平遥期中) 阅读下面解题过程，再解答后面的问题．
学习了一元一次不等式组的解法，老师给同学们布置了一个任务，请大家探究并求出不等式 $\text{[math]}$ 的解集．

小丽类比有理数的乘法法则，根据“同号两数相乘，积为正”可以得到：① $\text{[math]}$ 或② $\text{[math]}$ ，解不等式组①得 $\text{[math]}$ ，解不等式组②得 $\text{[math]}$ ，所以原不等式解集为 $\text{[math]}$ 或 $\text{[math]}$ ．请你仿照上述方法，求不等式的 $\text{[math]}$ 的解集．

答案解析收藏纠错 + 选题
13. (2023八上·东阳月考) 新定义：若一元一次方程的解在一元一次不等式组解集范围内，则称该一元一次方程为该不等式组的“关联方程”，例如：方程x-1=3的解为x=4，而不等式组 $\text{[math]}$ 的解集为2<x<5，不难发现x=4在2<x<5的范围内，所以方程x-1=3是不等式组 $\text{[math]}$ 的“关联方程”．
1. （1）在方程①2(x+1)-x=-3；② $\text{[math]}$ -1=x；③2x-7=0中，不等式组 $\text{[math]}$ 的“关联方程”是(填序号)
2. （2）关于x的方程2x-k=6是不等式组 $\text{[math]}$ 的“关联方程”，求k的取值范围；
3. （3）若关于x的方程 $\text{[math]}$ -3m=0是关于x的不等式组 $\text{[math]}$ 的“关联方程”，且此时不等式组有3个整数解，试求m的取值范围．
答案解析收藏纠错 + 选题
14. (2022八上·鄞州期中) 阅读以下材料：对于三个数a ， b ， c ，用M{a ， b ， c}表示这三个数的平均数，用min{a、b ， c}表示这三个数中最小的数．例如：M{﹣1，2，3}＝ $\text{[math]}$ ， min{-1，2，3}＝﹣1；min{﹣1，2，a}＝ $\text{[math]}$ 解决下列问题：
1. （1） min{ $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ }＝，若min{2，2x+2，4﹣2x}＝2，则x的范围为；
2. （2） ①如果M{2，x+1，2x}＝min{2，x+1，2x}，求x；
  ②根据①，你发现了结论“如果M{a ， b ， c}＝min{a ， b ， c}，那么（填a ， b ， c的大小关系）”．证明你发现的结论；
  ③运用②的结论，填空：若M{2x+y+2，x+2y ， 2x﹣y}＝min{2x+y+2，x+2y，2x﹣y}，则x+y＝．
答案解析收藏纠错 + 选题
15. (2023八上·东阳期中) 新定义：若一元一次方程的解在一元一次不等式组解集范围内，则称该一元一次方程为该不等式组的“关联方程”，例如：方程 $\text{[math]}$ 的解为 $\text{[math]}$ ，而不等式组 $\text{[math]}$ 的解集为 $\text{[math]}$ ，不难发现 $\text{[math]}$ 在 $\text{[math]}$ 的范围内，所以方程 $\text{[math]}$ 是不等式组 $\text{[math]}$ 的“关联方程”．
1. （1）在方程① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ 中，不等式组 $\text{[math]}$ 的“关联方程”是；（填序号）
2. （2）关于x的方程 $\text{[math]}$ 是不等式组 $\text{[math]}$ 的“关联方程”，求k的取值范围；
3. （3）若关于x的方程 $\text{[math]}$ 是关于x的不等式组 $\text{[math]}$ 的“关联方程”，且此时不等式组有3个整数解，试求m的取值范围．
答案解析收藏纠错 + 选题
16. (2023七上·温岭期中) 阅读下列材料：
我们给出如下定义：数轴上给定不重合两点A ， B ，若数轴上存在点M ，使得点M到点A的距离等于点M到点B的距离的2倍，则称点M为点A与点B的“亚运点”．其中在A，B之间的点M为点A与点B的“亚运@未来点”
解答下列问题：
1. （1）若点A表示的数为-5，点B表示的数为1，点M为点A与点B的“亚运点”，则点M表示的数为；
2. （2）若A、B两点的“亚运点”M表示的数为2，且A、B两点的距离为9（A在B的左侧），则点A表示的数为，
3. （3）点A表示的数为-6，点C ， D表示的数分别是-2，0，点O为数轴原点（与静止时的D点重合），点B为线段CD上一点（点B可以与点C与点D重合）．
  ①设点M表示的数为m ，若点M可以为点A与点B的“亚运@未来点”，则m可取得整数有；
  ②若点A和点D同时以每秒2个单位长度的速度向数轴正半轴方向移动．设移动的时间为t（t＞0）秒，当t的整数值为时，点O可以为点A与点B的“亚运@未来点”．
答案解析收藏纠错 + 选题
17. (2024七下·南昌期中) 定义：若一元一次方程的解在一元一次不等式的解集范围内，则称一元一次方程为一元一次不等式的“伴随方程”．如：一元一次方程 $\text{[math]}$ 的解为 $\text{[math]}$ ，而一元一次不等式 $\text{[math]}$ 的解集为 $\text{[math]}$ ，不难发现 $\text{[math]}$ 在 $\text{[math]}$ 范围内，则一元一次方程 $\text{[math]}$ 是一元一次不等式 $\text{[math]}$ 的“伴随方程”
1. （1）在① $\text{[math]}$ ， ② $\text{[math]}$ ， ③ $\text{[math]}$ 三个一元一次方程中，是一元一次不等式 $\text{[math]}$ 的“伴随方程”的有（填序号）；
2. （2）若关于x的一元一次方程 $\text{[math]}$ 是关于x一元一次不等式 $\text{[math]}$ 的“伴随方程”，且一元一次方程 $\text{[math]}$ 不是关于x的一元一次不等式 $\text{[math]}$ 的“伴随方程”．
  ①求a的取值范围；
  
  ②直接写出代数式 $\text{[math]}$ 的最大值．
答案解析收藏纠错 + 选题
18. (2023七下·江汉期末) 定义运算： $\text{[math]}$ ，已知 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）直接写出： $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）若关于 $\text{[math]}$ 的不等式组 $\text{[math]}$ 无解，求 $\text{[math]}$ 的取值范围；
3. （3）若 $\text{[math]}$ 的解集为 $\text{[math]}$ ，求不等式 $\text{[math]}$ 的解集．
答案解析收藏纠错 + 选题
19. [阅读理解]
∵ $\text{[math]}$ < $\text{[math]}$ < $\text{[math]}$ ，即2< $\text{[math]}$ <3．

∴ $\text{[math]}$ 的整数部分为2，小数部分为 $\text{[math]}$ - 2，

∴1< $\text{[math]}$ -1<2，

∴ $\text{[math]}$ -1的整数部分为1，小数部分为 $\text{[math]}$ -2．

[解决问题]已知a是 $\text{[math]}$ -2的整数部分，b是 $\text{[math]}$ -3的小数部分，求：
1. （1） a，b的值．
2. （2） (b+4)²-(-a)³的平方根．
答案解析收藏纠错 + 选题
20. (2023八上·福州开学考) 深化理解：
新定义：对非负实数 $\text{[math]}$ “四舍五入”到个位的值记为 $\text{[math]}$ ，即：当 $\text{[math]}$ 为非负整数时，如果 $\text{[math]}$ ，则 $\text{[math]}$ ；
反之，当 $\text{[math]}$ 为非负整数时，如果 $\text{[math]}$ ，则 $\text{[math]}$ ．
例如： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$
试解决下列问题：
1. （1）填空： $\text{[math]}$ ▲ ， $\text{[math]}$ ▲ $\text{[math]}$ 为圆周率 $\text{[math]}$ ， $\text{[math]}$ ▲ ；
  $\text{[math]}$ 如果 $\text{[math]}$ ，求实数 $\text{[math]}$ 的取值范围；
2. （2）若关于 $\text{[math]}$ 的不等式组 $\text{[math]}$ 的整数解恰有 $\text{[math]}$ 个，求 $\text{[math]}$ 的取值范围；
3. （3）求满足 $\text{[math]}$ 的所有非负实数 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
21. (2023七下·长沙期末) 阅读理解：
定义：使方程（组）与不等式（组）同时成立的未知数的值称为此方程（组）和不等式（组）的“理想解”．例如：已知方程 $\text{[math]}$ 与不等式 $\text{[math]}$ ，当 $\text{[math]}$ 时， $\text{[math]}$ ， $\text{[math]}$ 同时成立，则称“ $\text{[math]}$ ”是方程 $\text{[math]}$ 与不等式 $\text{[math]}$ 的“理想解”．

问题解决：
1. （1）请判断方程 $\text{[math]}$ 的解是此方程与以下哪些不等式（组）的“理想解”（直接填写序号）
  ① $\text{[math]}$ ，
  ② $\text{[math]}$ ，
  ③ $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ 是方程组 $\text{[math]}$ 与不等式 $\text{[math]}$ 的“理想解”，求q的取值范围；
3. （3）当 $\text{[math]}$ 时，方程 $\text{[math]}$ 的解都是此方程与不等式 $\text{[math]}$ 的“理想解”．若 $\text{[math]}$ 且满足条件的整数n有且只有一个，求m的取值范围．
答案解析收藏纠错 + 选题

四、数形结合探究题

22. (2022七下·周村期末) 阅读下列材料：
小明在一本数学杂志上看到一道有意思的数学题：解不等式 $\text{[math]}$ ，根据绝对值的几何意义，到原点距离小于1的点在数轴上集中在－1和＋1之间，如图：
所以，该不等式的解集为 $\text{[math]}$ ．
因此，不等式 $\text{[math]}$ 的解集为 $\text{[math]}$ 或 $\text{[math]}$ ．
根据以上方法小明继续探究了不等式 $\text{[math]}$ 的解集，即到原点的距离大于2小于5的点的集合就集中在这样的区域内，如图：
所以，不等式的解集为－5＜x＜－2或2＜x＜5．
仿照小明的做法解决下面问题：
1. （1）不等式 $\text{[math]}$ 的解集为；
2. （2）不等式 $\text{[math]}$ 的解集是；
3. （3）不等式 $\text{[math]}$ 的解集是．
答案解析收藏纠错 + 选题
23. (2022七下·安庆期中) 阅读：我们知道， $\text{[math]}$ 于是要解不等式 $\text{[math]}$ ，我们可以分两种情况去掉绝对值符号，转化为我们熟悉的不等式，按上述思路，我们有以下解法：
解：⑴当 $\text{[math]}$ ，即 $\text{[math]}$ 时： $\text{[math]}$
解这个不等式，得： $\text{[math]}$
由条件 $\text{[math]}$ ，有： $\text{[math]}$
⑵当 $\text{[math]}$ ，即 $\text{[math]}$ 时， $\text{[math]}$
解这个不等式，得： $\text{[math]}$
由条件 $\text{[math]}$ ，有： $\text{[math]}$
∴如图，综合（1）、（2）原不等式的解为 $\text{[math]}$
根据以上思想，请探究完成下列2个小题：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
24. (2020七下·北京期末) 在数学课外小组活动中，老师提出了如下问题：
如果一个不等式中含有绝对值，并且绝对值符号中含有未知数，我们把这个不等式叫做绝对值不等式，求绝对值不等式|x|＞a（a>0）和|x|＜a（a>0）的解集．

小明同学的探究过程如下：

先从特殊情况入手，求|x|＞2和|x|＜2的解集．确定|x|＞2的解集过程如下：

先根据绝对值的几何定义，在数轴上找到到原点的距离大于2的所有点所表示的数，在数轴上确定范围如下：
1. （1）请将小明的探究过程补充完整；
  所以，|x|＞2的解集是x＞2或．
  
  再来确定|x|＜2的解集：同样根据绝对值的几何定义，在数轴上找到到原点的距离小于2的所有点所表示的数，在数轴上确定范围如下：
  
  所以，|x|＜2的解集为：．
  
  经过大量特殊实例的实验，小明得到绝对值不等式|x|＞a（a>0）的解集为，|x|＜a（a>0）的解集为．
  
  请你根据小明的探究过程及得出的结论，解决下列问题：
2. （2）求绝对值不等式2|x+1|-3＜5的解集．
答案解析收藏纠错 + 选题

五、实践探究题

25. (2023九下·瑞安开学考) 根据以下素材，完成探索任务.

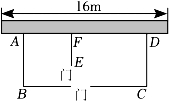
问题的提出

根据以下提供的素材，在总费用（新墙的建筑费用与门的价格和）不高于6400元的情况下，如何设计最大饲养室面积的方案？

素材1：图1是某农场拟建两间矩形饲养室，饲养室的一面靠现有墙，中间用一道墙隔开，计划中建筑材料可建围墙的总长为20m，开2个门，且门宽均为1m.

素材2：2个门要求同一型号，有关门的采购信息如表.

如表

型号	A	B	C
规格（门宽）	1米	1.2米	1米
单价（元）	250	280	300

素材3：与现有墙平行方向的墙建筑费用为400元/米，与现有墙垂直方向的墙建筑费用为200元/米.

问题解决

任务1

确定饲养室的形状

设AB＝x，矩形ABCD的面积为S，求S关于x的函数表达式.

任务2

探究自变量x的取值范围.

任务3

确定设计方案

我的设计方案是选型号▲ 门，AB＝▲ m，BC＝▲ m，S的最大值为▲ m².

答案解析收藏纠错 + 选题

26. (2017八下·重庆期中) 某景区内的环形路是边长为800米的正方形ABCD，如图1和图2．现有1号、2号两游览车分别从出口A和景点C同时出发，1号车顺时针、2号车逆时针沿环形路连续循环行驶，供游客随时免费乘车（上、下车的时间忽略不计），两车速度均为200米/分．
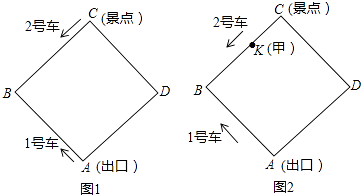
探究：设行驶吋间为t分．
1. （1）当0≤t≤8时，分别写出1号车、2号车在左半环线离出口A的路程y₁ ， y₂（米）与t（分）的函数关系式，并求出当两车相距的路程是400米时t的值；
2. （2） t为何值时，1号车第三次恰好经过景点C？并直接写出这一段时间内它与2号车相遇过的次数．
3. （3）发现：如图2，游客甲在BC上的一点K（不与点B，C重合）处候车，准备乘车到出口A，设CK=x米．
  情况一：若他刚好错过2号车，便搭乘即将到来的1号车；
  情况二：若他刚好错过1号车，便搭乘即将到来的2号车．
  比较哪种情况用时较多？（含候车时间）
  决策：已知游客乙在DA上从D向出口A走去．步行的速度是50米/分．当行进到DA上一点P （不与点D，A重合）时，刚好与2号车迎面相遇．
  他发现，乘1号车会比乘2号车到出口A用时少，请你简要说明理由：
4. （4）设PA=s（0＜s＜800）米．若他想尽快到达出口A，根据s的大小，在等候乘1号车还是步行这两种方式中．他该如何选择？
答案解析收藏纠错 + 选题
27. (2024八上·讷河期末) 综合与实践问题情境：“文房四宝”是中国独有的书法绘画工具，即笔、墨、纸、砚，文房四宝之名，起源于南北朝时期．某中学为了落实双减政策，丰富学生的课后服务活动，开设了书法社团，计划为学生购买A，B两种型号“文房四宝”共40套．已知某文化用品店每套A型号的“文房四宝”的标价比B型号的“文房四宝”的标价高30%，若按标价购买需花费4300元，其中购买B型号“文房四宝”花费3000元．
问题解决：
1. （1）求每套B型号的“文房四宝”的标价．
2. （2）若经过与店主协商，考虑到购买较多，店主同意该中学按A型号“文房四宝”九折，B型号“文房四宝”八折的优惠价购入，则购买原定数量的A，B型号“文房四宝”共需花费多少元？
3. （3）一段时间后，由于传统文化广受关注，另一所学校想要购入A，B两种型号“文房四宝”共100套。店主继续以（2）中的折扣价进行销售，已知A，B两种型号的“文房四宝”每套进价分别为67元和50元，若通过此单生意，该店主获利不低于3800元，则该校在这家店至少买了套A型“文房四宝”？
答案解析收藏纠错 + 选题
28. (2024八上·防城期末) 【综合与实践】
学校在某商场购买甲、乙两种不同类型的足球，相关信息如下：购买甲种足球共用2000元，购买乙种足球共花费1400元.已知购买一个乙种足球比购买一个甲种足球多花20元.设购买一个甲种足球的单价是 $\text{[math]}$ 元。
1. （1）请用含 $\text{[math]}$ 的代数式分别表示购买甲、乙两种足球的数量；
2. （2）若本次购买甲种足球的数量是购买乙种足球数量的2倍，求甲、乙两种足球在此商场的销售单价；
3. （3）为满足学生需求，这所学校决定再次购买甲、乙两种足球共50个.恰逢该商场对两种足球的销售单价进行调整，甲种足球的销售单价比上次购买时提高了10％，乙种足球的销售单价比上次购买时降低了10％.如果此次购买甲、乙两种足球的总费用不超过2950元，求这所学校最多可以购买乙种足球的数量.
答案解析收藏纠错 + 选题
29. (2023七下·洪洞期末) 课堂上，老师设计了“接力游戏”，规则：一列同学每人只完成解不等式的一步变形，即前一个同学完成一步，后一个同学接着前一个同学的步骤进行下一步变形，直至解出不等式的解集．请根据下面的“接力游戏”回答问题．
1. （1）任务一：①在“接力游戏”中，乙同学是根据进行变形的．
  A．等式的基本性质
  B．不等式的基本性质
  C．乘法对加法的分配律
  ②在“接力游戏”中，出现错误的是同学，这一步错误的原因是．
2. （2）任务二：在“接力游戏”中该不等式的正确解集是．
3. （3）任务三：除纠正上述错误外，请你根据平时的学习经验，针对解不等式时还需要注意的事项给同学们提一条建议．
  接力游戏
  老师 $\text{[math]}$
  甲同学 $\text{[math]}$
  乙同学 $\text{[math]}$
  丙同学 $\text{[math]}$
  丁同学 $\text{[math]}$
  戊同学 $\text{[math]}$
答案解析收藏纠错 + 选题
30. (2019·镇江) 学校数学兴趣小组利用机器人开展数学活动.在相距 $\text{[math]}$ 个单位长度的直线跑道 $\text{[math]}$ 上，机器人甲从端点 $\text{[math]}$ 出发，匀速往返于端点 $\text{[math]}$ 、 $\text{[math]}$ 之间，机器人乙同时从端点 $\text{[math]}$ 出发，以大于甲的速度匀速往返于端点 $\text{[math]}$ 、 $\text{[math]}$ 之间.他们到达端点后立即转身折返，用时忽略不计.兴趣小组成员探究这两个机器人迎面相遇的情况，这里的“迎面相遇”包括面对面相遇、在端点处相遇这两种.
1. （1）【观察】
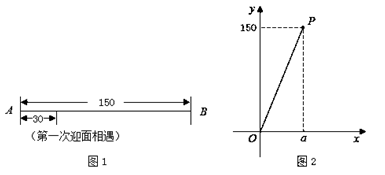
  ①观察图 $\text{[math]}$ ，若这两个机器人第一次迎面相遇时，相遇地点与点 $\text{[math]}$ 之间的距离为 $\text{[math]}$ 个单位长度，则他们第二次迎面相遇时，相遇地点与点 $\text{[math]}$ 之间的距离为个单位长度；
  
  ②若这两个机器人第一次迎面相遇时，相遇地点与点 $\text{[math]}$ 之间的距离为 $\text{[math]}$ 个单位长度，则他们第二次迎面相遇时，相遇地点与点 $\text{[math]}$ 之间的距离为个单位长度；
2. （2）【发现】
  设这两个机器人第一次迎面相遇时，相遇地点与点 $\text{[math]}$ 之间的距离为 $\text{[math]}$ 个单位长度，他们第二次迎面相遇时，相遇地点与点 $\text{[math]}$ 之间的距离为 $\text{[math]}$ 个单位长度.兴趣小组成员发现了 $\text{[math]}$ 与 $\text{[math]}$ 的函数关系，并画出了部分函数图象（线段 $\text{[math]}$ ，不包括点 $\text{[math]}$ ，如图 $\text{[math]}$ 所示）.
  
  ① $\text{[math]}$ ＝；
  
  ②分别求出各部分图象对应的函数表达式，并在图 $\text{[math]}$ 中补全函数图象；
3. （3）【拓展】
  设这两个机器人第一次迎面相遇时，相遇地点与点 $\text{[math]}$ 之间的距离为 $\text{[math]}$ 个单位长度，他们第三次迎面相遇时，相遇地点与点 $\text{[math]}$ 之间的距离为 $\text{[math]}$ 个单位长度.若这两个机器人第三次迎面相遇时，相遇地点与点 $\text{[math]}$ 之间的距离 $\text{[math]}$ 不超过 $\text{[math]}$ 个单位长度，则他们第一次迎面相遇时，相遇地点与点 $\text{[math]}$ 之间的距离 $\text{[math]}$ 的取值范围是.（直接写出结果）
答案解析收藏纠错 + 选题