2024年浙教版数学七（下）微素养核心突破3 平行线的判定与...

更新时间：2024-04-18 浏览次数：43 类型：复习试卷

一、选择题

1. 将一直角三角板与两边平行的纸条如图所示放置，若∠1=55°，则∠2的度数为（）

A . 135° B . 130° C . 45° D . 35°

答案解析收藏纠错 + 选题
2. (2023七下·温州期末) 一副分别含 $\text{[math]}$ 和 $\text{[math]}$ 的三角板如图所示摆放.若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023七下·上虞期末) 如图，直线 $\text{[math]}$ ，一块三角板的直角顶点在直线 $\text{[math]}$ 上，两直角边均与直线 $\text{[math]}$ 相交，若 $\text{[math]}$ ，则 $\text{[math]}$ ＝（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023七下·义乌月考) 如图，将三角板与直尺贴在一起，使三角板的直角顶点C（∠ACB＝90°）在直尺的一边上，若∠2＝65°，则∠1的度数是（）

A . 15° B . 25° C . 35° D . 65°

答案解析收藏纠错 + 选题
5. (2023七下·海曙期末) 直角三角板和直尺如图放置，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023七下·常山期末) 若将一副三角板按如图的方式放置，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024七下·杭州期中) 在同一平面内，将两个完全相同的三角板按如图摆放，可以画出两条互相平行的直线 $\text{[math]}$ 与 $\text{[math]}$ ．这样画的依据是（）

A . 内错角相等，两直线平行 B . 同位角相等，两直线平行 C . 两直线平行，同位角相等 D . 两直线平行，内错角相等

答案解析收藏纠错 + 选题
8. 一把直尺和一块含30°角的直角三角板ABC按如图方式摆放，直尺一边与三角板的两直角边分别交于点D和点E，另一边与三角板的两直角边分别交于点F和点A，且∠CED=35°，那么∠BAF的大小为（）

A . 5° B . 15° C . 25° D . 35°

答案解析收藏纠错 + 选题
9. 如图l₁∥l₂点О在直线l₁上，将三角板的直角顶点放在点О处，三角板的两条直角边与l₂交于A，B两点，若∠1=35°，则∠2的度数为（）

A . 35° B . 45° C . 55° D . 65°

答案解析收藏纠错 + 选题
10. (2024七下·恩施月考) 将一副三角板如图放置，则下列结论中，正确的是（）
① $\text{[math]}$ ；②如果 $\text{[math]}$ ，则有 $\text{[math]}$ ；③如果 $\text{[math]}$ ，则有 $\text{[math]}$ ；④如果 $\text{[math]}$ ，则有 $\text{[math]}$ ．

A . ①②③④ B . ③④ C . ①②④ D . ①②③

答案解析收藏纠错 + 选题

二、填空题

11. (2023七下·鄞州月考) 如图，把一块直角三角板的直角顶点放在直尺的一边上，如果 $\text{[math]}$ ，那么 $\text{[math]}$ 的度数为.

答案解析收藏纠错 + 选题
12. (2022七下·洞头期中) 一直角三角板的直角顶点恰好放在直尺的边缘线上（如图所示），若 $\text{[math]}$ ，则 $\text{[math]}$ 度.

答案解析收藏纠错 + 选题
13. (2022七下·杭州期中) 如图，把一块三角板的 $\text{[math]}$ 角的顶点放在直尺的一边上，若 $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ .

答案解析收藏纠错 + 选题
14. 如图所示，直线 $\text{[math]}$ ，三角板的直角顶点 $\text{[math]}$ 落在直线 $\text{[math]}$ 上，两条直角边分別交直线 $\text{[math]}$ 于B，C两点.若 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
15. (2021七下·余姚竞赛) 将一把直尺和一块直角三角板如图放置，如果∠α=43°，则∠β的度数是度．

答案解析收藏纠错 + 选题
16. (2019七下·东阳期末) 将一副三角板按如图放置，则下列结论：①∠1=∠3；②如果∠2=30°，则有AC∥DE；③如果∠1=60°，则有BC∥AD④如果∠2=45°，必有∠4=∠C其中正确的有。

答案解析收藏纠错 + 选题

三、解答题

17. (2023七下·大田期中) 如图1，直线 $\text{[math]}$ 与直线 $\text{[math]}$ 交于点O， $\text{[math]}$ （ $\text{[math]}$ ）.小明将一个含 $\text{[math]}$ ， $\text{[math]}$ 的直角三角板 $\text{[math]}$ 如图1所示放置，使顶点P落在直线 $\text{[math]}$ 上，过点Q作直线 $\text{[math]}$ 交直线 $\text{[math]}$ 于点H（点H在Q左侧）.
1. （1）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数.
2. （2）如图2，若 $\text{[math]}$ 的角平分线交直线 $\text{[math]}$ 于点E.
  ①当 $\text{[math]}$ ， $\text{[math]}$ 时，求证： $\text{[math]}$ .
  ②小明将三角板保持 $\text{[math]}$ 并向左平移，运动过程中，探究 $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系，并说明理由.
答案解析收藏纠错 + 选题
18. (2022八上·太原期中) 综合与实践
问题情境：
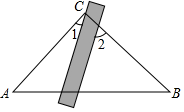
数学课上，老师让同学们以“三角板与平行线”为主题开展数学活动．如图1，已知l₁∥l₂ ，直角三角板ABC中，∠B＝90°，将其顶点A放在直线l₂上，并使边AB⊥直线l₁于点D，AC与l₁相交于点H．老师提出问题：试判断边BC与直线l₁的位置关系并说明理由．
1. （1）请解答老师提出的问题：
2. （2）如图2，将图1中三角板ABC的直角顶点B放在平行线之间，两直角边AB，CB分别与l₁_，l₂相交于点P，Q，得到∠1和∠2，试探究∠1与∠2的数量关系并说明理由．
  下面是小亮不完整的解答过程和解题反思，请你补充完整：
  解：∠1＋∠2＝90°．过点B作直线BN∥l₁ ，如图：
  ∵l₁∥l₂（已知）
  ∴BN∥l₂（                ）
  ∴∠1=  ▲  ∠2=  ▲  （                ）
  ∵∠  ▲  +∠   ▲  =∠ABC，∠ABC=90°
  ∴∠1＋∠2＝90°
  解题反思：在图中“过点B作直线BN∥l₁”的作用是  ▲
3. （3）受小亮启发，同学们续探究下列问题．
  请从下列A，B两题中任选一题作答．我选择 ▲
  A．在图2中作线段PO和QO，使它们分别平分∠1和∠2的对顶角，如图3．直接写出∠POQ的度数．
  B．在图2中∠ABC内部作射线BE，过点B作射线BF⊥BE交直线L₂于点M，得到∠3，如图4．直接写出∠1，∠3与∠EBC的数量关系．
答案解析收藏纠错 + 选题
19. (2021七下·诸暨期末) 如图，直线 $\text{[math]}$ 直线 $\text{[math]}$ ，一块三角板的顶点 $\text{[math]}$ 在直线 $\text{[math]}$ 上，边 $\text{[math]}$ 、 $\text{[math]}$ 分别交直线 $\text{[math]}$ 于 $\text{[math]}$ 、 $\text{[math]}$ 两点. $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
1. （1）如图1， $\text{[math]}$ ，则
  ① $\text{[math]}$ ▲ °；
  
  ②若 $\text{[math]}$ 与 $\text{[math]}$ 的角平分线交于点 $\text{[math]}$ ，则 $\text{[math]}$ ▲ °.
2. （2）如图2，点 $\text{[math]}$ 在 $\text{[math]}$ 的平分线上，连 $\text{[math]}$ ，且 $\text{[math]}$ ，若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数.
3. （3）如图3，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ °（用含 $\text{[math]}$ 的式子表示）.
答案解析收藏纠错 + 选题
20. (2023七下·江津期中) 已知三角板 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，长方形DEFG中， $\text{[math]}$ ．将三角板 $\text{[math]}$ 的顶点A放在长方形的边 $\text{[math]}$ 上， $\text{[math]}$ 与 $\text{[math]}$ 相交于点M．
1. （1）如图1，若 $\text{[math]}$ 于点N，则 $\text{[math]}$ 的度数是， $\text{[math]}$ 的度数是；
2. （2）如图2，请你猜想并写出 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系，并说明理由；
3. （3）请你总结（1），（2）的思路，在图3中探究 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系？请直接写出数量关系．
答案解析收藏纠错 + 选题
21. (2023七下·顺德期中) 将一副三角板中的两个直角顶点 $\text{[math]}$ 叠放在一起，其中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$
1. （1）操作发现：如图1，当点 $\text{[math]}$ 落在线段 $\text{[math]}$ 上时，写出图中相等的角（写出三对即可）；
2. （2）问题解决：如图2，若线段 $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ．
  ①若 $\text{[math]}$ 时，求 $\text{[math]}$ 的度数；
  ②当 $\text{[math]}$ 为何值时，使线段 $\text{[math]}$ 最短；
3. （3）深化拓展：如图3，将三角板 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针转动，直到边 $\text{[math]}$ 与 $\text{[math]}$ 重合即停止，转动的过程中当两块三角板恰有两边平行时，请直接写出 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题
22. (2023八下·毕节期末) 如图1，直线 $\text{[math]}$ ，直线 $\text{[math]}$ 与 $\text{[math]}$ ， $\text{[math]}$ 分别交于点G，H， $\text{[math]}$ ．将一个直角三角板 $\text{[math]}$ 按如图1所示放置，使点N，M分别在直线 $\text{[math]}$ ， $\text{[math]}$ 上，且在点G，H的右侧，已知 $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为；
2. （2）若 $\text{[math]}$ ，对 $\text{[math]}$ 说明理由；
3. （3）如图2，已知 $\text{[math]}$ 的平分线 $\text{[math]}$ 交直线 $\text{[math]}$ 于点O．
  ①当 $\text{[math]}$ ， $\text{[math]}$ 时，求 $\text{[math]}$ 的值；
  ②现将三角板 $\text{[math]}$ 保持 $\text{[math]}$ ，并沿直线 $\text{[math]}$ 向左平移，在平移的过程中，直接写出 $\text{[math]}$ 的度数（用含 $\text{[math]}$ 的代数式表示）．
答案解析收藏纠错 + 选题
23. (2023七下·石家庄期中) 题目：“如图1，已知 $\text{[math]}$ 内有一点P，射线 $\text{[math]}$ ，且与 $\text{[math]}$ 交于点E，过点P画射线 $\text{[math]}$ 平行于 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 相交于点H．”嘉嘉用两个完全一样的三角板进行画图，画图过程如图2所示．
1. （1）嘉嘉的画图依据是；
2. （2）淇淇看了嘉嘉画出的图形后，对 $\text{[math]}$ 进行了如下说理．请你补全淇淇的说理过程；
  ∵ $\text{[math]}$ （已知），
  ∴ $\text{[math]}$ ▲ （）．
  ∵ $\text{[math]}$ $\text{[math]}$ （已知），
  ∴ $\text{[math]}$ ▲ （），
  ∴ $\text{[math]}$ （等量代换）；
3. （3）小明看了（2）中淇淇的说理过程后，认为说法“若两个角的两边分别平行，则这两个角相等”正确，请你判断小明的说法是否正确，并说明理由．
答案解析收藏纠错 + 选题
24. (2023七下·兰州期中) 问题情境
我们知道“如果两条平行线被第三条直线所截，所截得的同位角相等，内错角相等，同旁内角互补”，所以在某些探究性问题中通过“构造平行线”可以起到转化角的作用．

已知三角板ABC中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，长方形DEFG中， $\text{[math]}$ ．

问题初探

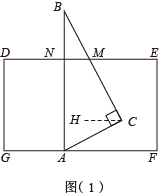
如图（1），若将三角板ABC的顶点A放在长方形的边GF上，BC与DE相交于点M， $\text{[math]}$ 于点N，则∠EMC的度数是多少呢？

此题有多种解答方法，下面是小军同学的分析过程：

过点C作 $\text{[math]}$ ，则 $\text{[math]}$ ，这样就将∠CAF转化为∠HCA，∠EMC转化为∠MCH，从而可以求得∠EMC的度数．
1. （1）请你直接写出 $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）类比再探
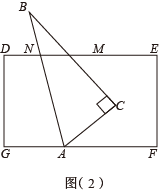
  若将三角板ABC按图（2）所示方式摆放（AB与DE不垂直），请你猜想∠EMC与∠CAF的数量关系，并说明理由；
3. （3）方法迁移
  请你总结（1）（2）解决问题的思路，在图（2）中探究∠BAG与∠BMD的数量关系，并直接写出结果．
答案解析收藏纠错 + 选题
25. (2024七下·修水期中) 综合与探究
数学活动课上，老师以“一个含 $\text{[math]}$ 的直角三角板和两条平行线”为背景展开探究活动，
如图1，已知直线 $\text{[math]}$ ，直角三角板 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）如图1，若 $\text{[math]}$ ，则 $\text{[math]}$ ；（直接写出答案）
2. （2） “启航”小组在图1的基础上继续展开探究：如图 $\text{[math]}$ ，调整三角板的位置，当三角板 $\text{[math]}$ 的直角顶点 $\text{[math]}$ 在直线 $\text{[math]}$ 上，直线 $\text{[math]}$ 与 $\text{[math]}$ ， $\text{[math]}$ 相交时，他们得出的结论是： $\text{[math]}$ ，你认为启航小组的结论是否正确，请说明理由；
3. （3）如图 $\text{[math]}$ ，受到“启航”小组的启发，“睿智”小组提出的问题是：在图 $\text{[math]}$ 的基础上，继续调整三角板的位置，当点 $\text{[math]}$ 不在直线 $\text{[math]}$ 上，直线 $\text{[math]}$ 与 $\text{[math]}$ ， $\text{[math]}$ 相交时， $\text{[math]}$ 与 $\text{[math]}$ 有怎样的数量关系？请你用平行线的知识说明理由．
答案解析收藏纠错 + 选题